Sorting Algorithms On 2 algorithms On log n

Sorting Algorithms O(n 2) algorithms O(n log n) algorithms Something even better?

Sorting a frequently used process l l Nature tends towards disorder Human prefer order e. g. • address books • shopping lists • databases

Insertion sort – O(n 2) l l Commonly used for hand-sorting Use two lists – unsorted and sorted unsorted = input list (size = n) sorted = an empty list loop from i =0 to n-1 do sorted. insert. In. Order(unsorted[i]) l n loops o(n) You have just implemented insert. In. Order()

Bubble sort – O(n 2) l l Imagine an unsorted list held vertically Smaller values are “light” and bubble up void bubble. Sort() { int i, j; int last=current_size-1; for(i=0; i<last; i++) { fot(j=last; j>I; j--) { if(data[j] is less than data[j-1]) swap(j, j-1); } } }

Quicksort – the first O(n log n) algorithm (1962) l l l Using divide-andconquer technique Select a pivot, split list into 2 sublists: smaller and larger Repeat this to all sublists until sublist’s size is reduced to 1 pivot 5 2 1 9 3 8 7 2 1 3 5 9 8 7 1 2 3 5 8 7 9 1 2 3 5 7 8 9

Quicksort – average O(n log n) the worst case O(n 2) quicksort(int fm, int to) { int p; // pivot position if(fm < to) { p = partition(fm, to); quicksort(fm, p-1); quicksort(p+1, to); } } Time per level 5 2 1 9 3 8 7 O(n) 2 1 3 5 9 8 7 O(n) 1 2 3 5 8 7 9 O(n) 1 2 3 5 7 8 9 O(n) Total = O(n log n)

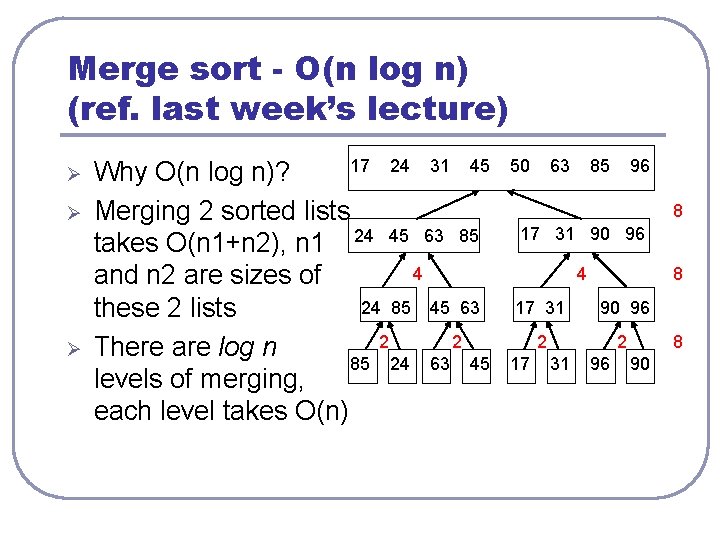
Merge sort - O(n log n) (ref. last week’s lecture) Ø Ø Ø 17 24 31 45 Why O(n log n)? Merging 2 sorted lists takes O(n 1+n 2), n 1 24 45 63 85 4 and n 2 are sizes of 24 85 45 63 these 2 lists 2 2 There are log n 85 24 63 45 levels of merging, each level takes O(n) 50 63 85 96 8 17 31 90 96 4 8 17 31 90 96 2 2 17 31 96 8 90

Can we have an O(n) sorting algorithm? Bucket-sort Yes, if we know the range of sorted items. Let the range be [1, k], If(k<O(n)), we can use extra momey A bag of coins to make k “buckets”. Then put each Total n item into the correct bucket. 8 We can do sorting without comparisons! Why O(n)? – only need go through n items once £ 2 2 1 1 p 3 2 p 4 5 p 5 10 p 6 20 p 7 50 p £ 1

Radix-sort - repeatedly apply Bucket-sort digit-by-digit An example – assume that we know sorted items are integers at most 3 digits (i. e. less than 1000) Input list – 314, 17, 802, 509, 87, 352, 199, 128. The 1 st phase: sorted by units 314 17 802 509 87 352 199 128 Input list By 1 st digit 10 buckets 0 1 2 3 4 5 6 7 8 9 join them 802 352 314 17 87 128 509 119

Radix-sort – cont. The 2 nd phase, sorted by 2 nd digit (tens). list from last phase – 802, 352, 314, 17, 87, 128, 509, 119. 802 352 314 17 87 128 509 119 list from last phase By 2 nd digit 0 1 2 3 4 5 6 7 8 9 join them 10 buckets 802 509 314 17 119 128 352 87

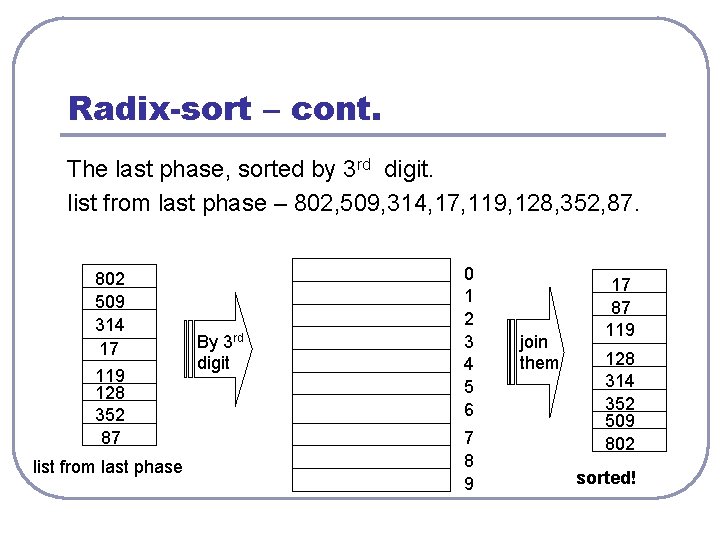
Radix-sort – cont. The last phase, sorted by 3 rd digit. list from last phase – 802, 509, 314, 17, 119, 128, 352, 87. 802 509 314 17 119 128 352 87 list from last phase By 3 rd digit 0 1 2 3 4 5 6 7 8 9 join them 17 87 119 128 314 352 509 802 sorted!

Radix-sort - nearly finished code Only for students having problem with Java programming! void radix. Sort() { int k, j; int b 0, b 1, b 2, b 3, b 4, b 5, b 6, b 7, b 8, b 9; // need 10 counters for 10 buckets // declare 10 buckets, B 0, B 2, ……, B 9 String[] B 0 = new String[limit]; …… // add other 9 more declarations for(k=1; k<5; k++) { // loop for digits. (we know that there are not more than 5 digits) b 0=b 1=b 2=b 3=b 4=b 5=b 6=b 7=b 8=b 9=0; // set all counter to 0 for(j=0; j<current_size; j++) { // loop for all items in the list, put them into correct buckets char c = Func. get. Nth. Digit(data[j], k); switch (c) { case '0': B 0[b 0++]=data[j]; break; . . . case '9': B 9[b 9++]=data[j]; break; } } // join the buckets j = 0; for(k=0; k<b 0; k++) data[j++] = B 0[k]; . . for(k=0; k<b 9; k++) data[j++] = B 9[k]; } }

Radix-sort l l l time complexity? O(n×k) where n is the length of the given list, k is the maximum number of digits used in the list To satisfy O(n×k) =< O(n log(n)), we need k =< log(n) Bucket-sort or Radix-sort – trade off between space and time

ng i m ti ins ert let ion de sorting divideconquer L L I S T A C K Q U E Time complexity L I S T binary search tree T R E E