Sorting Algorithms Merge and Quick Lecture Objectives Learn

Sorting Algorithms: Merge and Quick

Lecture Objectives • Learn how to implement the simple advanced sorting algorithms (merge and quick) • Learn how to implement the merge and quick sort algorithms • To learn how to estimate and compare the performance of divide and conquer sorting algorithms • To learn how to estimate and compare the performance of sorting algorithms

Merge Sort Algorithm • The merge sort algorithm sorts an array by: § Cutting the array in half § Recursively sorting each half § Merging the sorted halves • Dramatically faster than the selection, insertion and bubble sorts! • Applies the divide and conquer strategy
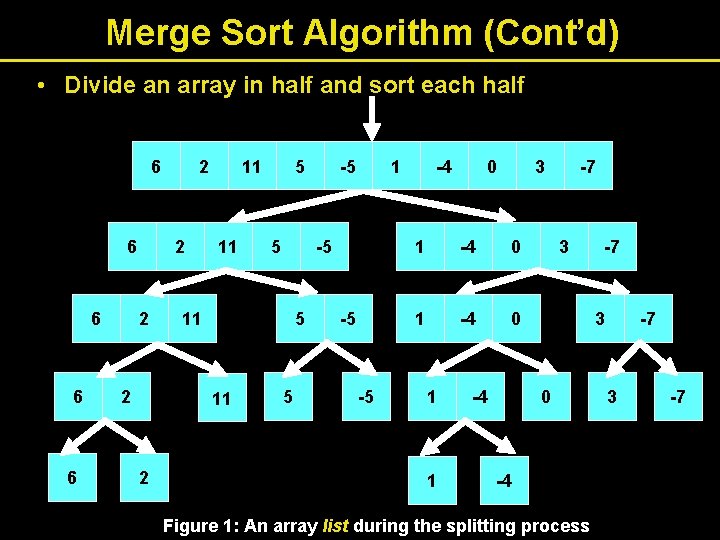
Merge Sort Algorithm (Cont’d) • Divide an array in half and sort each half 6 6 6 2 2 11 11 5 -5 11 2 5 5 -5 -5 -4 0 3 1 -4 0 1 1 -4 -7 3 0 -4 Figure 1: An array list during the splitting process -7 3 -7

Merge Sort Algorithm (Cont’d) • The merging of two sub-arrays is carried out as follows -7 -5 k 3 -5 2 k 1 5 6 k 1 -4 k 3 0 k 3 2 3 k 3 -7 11 k 1 k 2 5 k 3 -4 k 2 6 11 k 3 0 k 2 k 3 1 3 k 2 Figure 2: An array list during the splitting process k 2
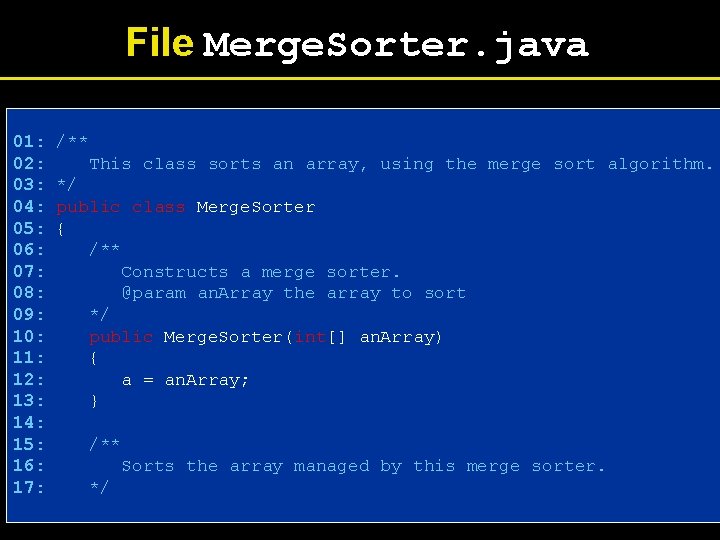
File Merge. Sorter. java 01: 02: 03: 04: 05: 06: 07: 08: 09: 10: 11: 12: 13: 14: 15: 16: 17: /** This class sorts an array, using the merge sort algorithm. */ public class Merge. Sorter { /** Constructs a merge sorter. @param an. Array the array to sort */ public Merge. Sorter(int[] an. Array) { a = an. Array; } /** Sorts the array managed by this merge sorter. */
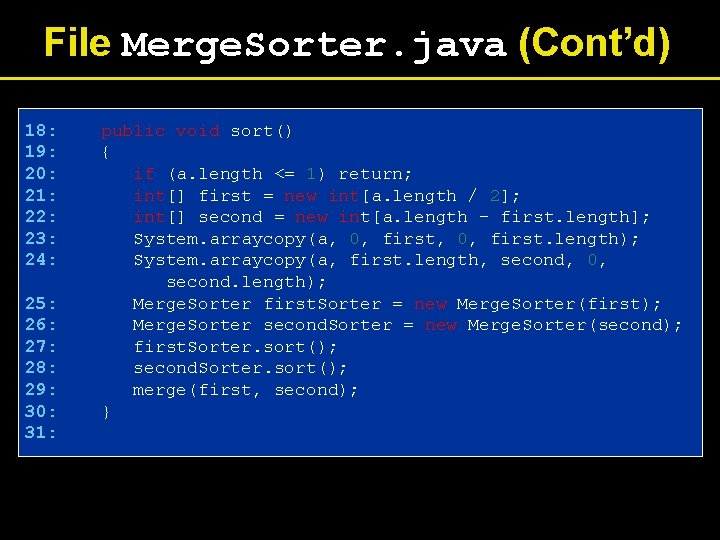
File Merge. Sorter. java (Cont’d) 18: 19: 20: 21: 22: 23: 24: 25: 26: 27: 28: 29: 30: 31: public void sort() { if (a. length <= 1) return; int[] first = new int[a. length / 2]; int[] second = new int[a. length - first. length]; System. arraycopy(a, 0, first. length); System. arraycopy(a, first. length, second, 0, second. length); Merge. Sorter first. Sorter = new Merge. Sorter(first); Merge. Sorter second. Sorter = new Merge. Sorter(second); first. Sorter. sort(); second. Sorter. sort(); merge(first, second); }

File Merge. Sorter. java (Cont’d) 32: 33: 34: 35: 36: 37: 38: 39: 40: 41: 42: 43: 44: 45: 46: 47: 48: /** Merges two sorted arrays into the array managed by this merge sorter. @param first the first sorted array @param second the second sorted array */ private void merge(int[] first, int[] second) { // Merge both halves into the temporary array int i. First = 0; // Next element to consider in the first array int i. Second = 0; // Next element to consider in the second array int j = 0; // Next open position in a
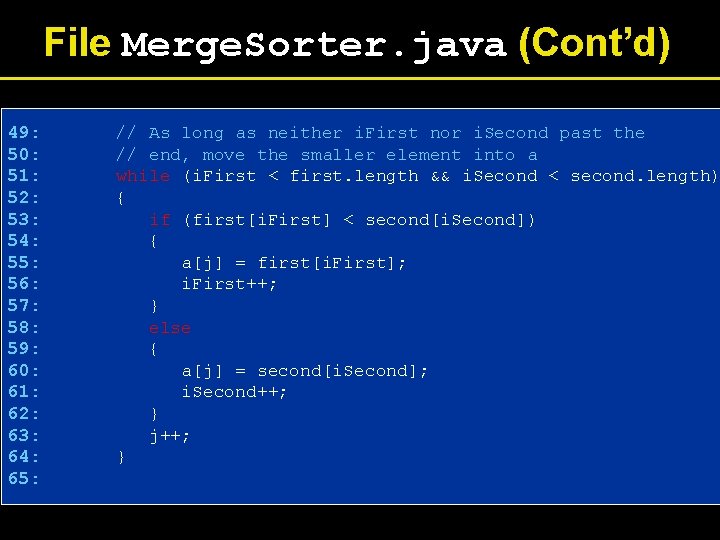
File Merge. Sorter. java (Cont’d) 49: 50: 51: 52: 53: 54: 55: 56: 57: 58: 59: 60: 61: 62: 63: 64: 65: // As long as neither i. First nor i. Second past the // end, move the smaller element into a while (i. First < first. length && i. Second < second. length) { if (first[i. First] < second[i. Second]) { a[j] = first[i. First]; i. First++; } else { a[j] = second[i. Second]; i. Second++; } j++; }
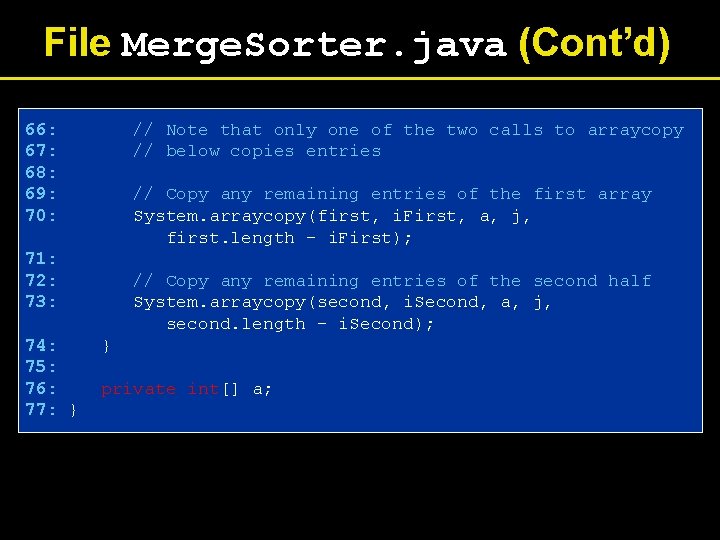
File Merge. Sorter. java (Cont’d) 66: 67: 68: 69: 70: // Note that only one of the two calls to arraycopy // below copies entries // Copy any remaining entries of the first array System. arraycopy(first, i. First, a, j, first. length - i. First); 71: 72: 73: 74: 75: 76: 77: } // Copy any remaining entries of the second half System. arraycopy(second, i. Second, a, j, second. length - i. Second); } private int[] a;
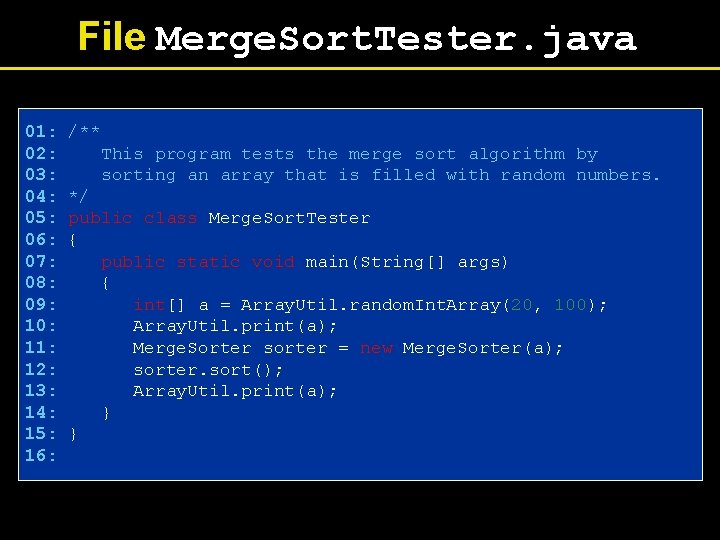
File Merge. Sort. Tester. java 01: 02: 03: 04: 05: 06: 07: 08: 09: 10: 11: 12: 13: 14: 15: 16: /** This program tests the merge sort algorithm by sorting an array that is filled with random numbers. */ public class Merge. Sort. Tester { public static void main(String[] args) { int[] a = Array. Util. random. Int. Array(20, 100); Array. Util. print(a); Merge. Sorter sorter = new Merge. Sorter(a); sorter. sort(); Array. Util. print(a); } }

File Merge. Sort. Tester. java (Cont’d) • Output: 8 81 48 53 46 70 98 42 27 76 33 24 2 76 62 89 90 5 13 21 2 5 8 13 21 24 27 33 42 46 48 53 62 70 76 76 81 89 90 98
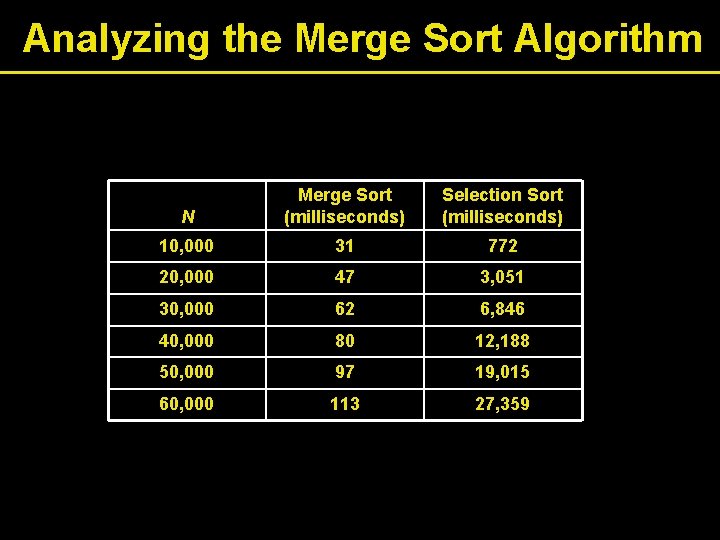
Analyzing the Merge Sort Algorithm N Merge Sort (milliseconds) Selection Sort (milliseconds) 10, 000 31 772 20, 000 47 3, 051 30, 000 62 6, 846 40, 000 80 12, 188 50, 000 97 19, 015 60, 000 113 27, 359
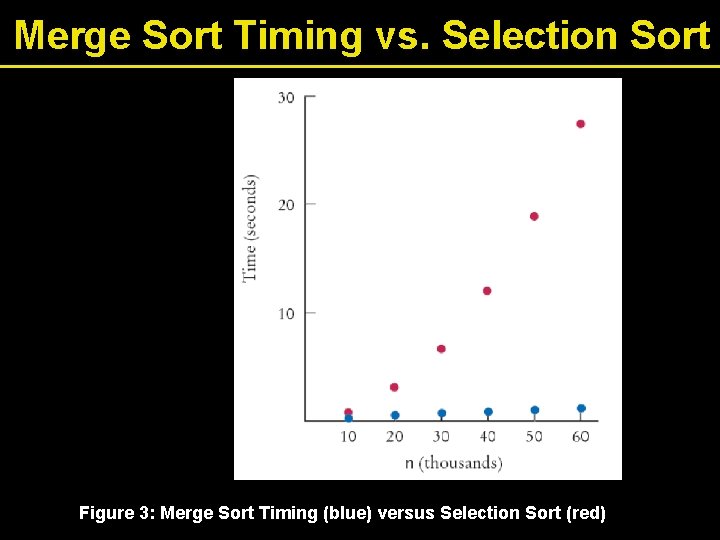
Merge Sort Timing vs. Selection Sort Figure 3: Merge Sort Timing (blue) versus Selection Sort (red)

Analyzing the Merge Sort Algorithm • In an array of size N, count how many times an array element is visited • Assume N is a power of 2: N = 2 m • Calculate the number of visits to create the two subarrays and then merge the two sorted arrays § 3 visits to merge each element or 3 N visits § 2 N visits to create the two sub-arrays § total of 5 N visits ! l a p O n o ti

Analyzing the Merge Sort Algorithm (Cont’d) • Let T(n) denote the number of visits to sort an array of n elements then § T(n) = T(n/2) + 5 n or § T(n) = 2 T(n/2) + 5 n • The visits for an array of size n/2 is: T(n/2) = 2 T(n/4) + 5 n/2 § So T(n) = 2 × 2 T(n/4) +5 n + 5 n • The visits for an array of size n/4 is: T(n/4) = 2 T(n/8) + 5 n/4 § So T(n) = 2 × 2 T(n/8) + 5 n ! l a p O n o ti

Analyzing the Merge Sort Algorithm (Cont’d) • Repeating the process k times: T(n) = 2 k. T(n/2 k) +5 nk • since N = 2 m, when k = m: T(n) = 2 m. T(n/2 m) +5 Nm • T(n) = N T(1) +5 Nm • T(n) = N + 5 N log 2(N) ! l a p O n o ti

Analyzing the Merge Sort Algorithm (Cont’d) • To establish growth order: § Drop the lower-order term N § Drop the constant factor 5 § Drop the base of the logarithm since all logarithms are related by a constant factor § We are left with N log(N) p O n o ti ! l a

Merge Sort Versus Selection Sort • Selection sort is a quadratic algorithm, i. e. , number of comparisons depends on N 2. • In the merge sort algorithm, the number of comparisons depends on Nlog(N). • The log(N) function grows much more slowly than N 2.

Sorting Using Java API • The Arrays class (Package: java. util ) implements a sorting method • To sort an array of integers int[] a = {2, -5, 3, 0, 7, -11}; Arrays. sort(a); • That sort() method uses a sophisticated fast sorting algorithm (is it the merge or quick sort? )

The Quick Sort Algorithm • Divide and conquer 1. Partition the range 2. Sort each partition

The Quick Sort Algorithm (Cont’d) public void sort(int from, int to) { if (from >= to) return; int p = partition(from, to); sort(from, p); sort(p + 1, to); }

The Quick Sort Algorithm (Cont’d) Figure 4: Partitioning a Range
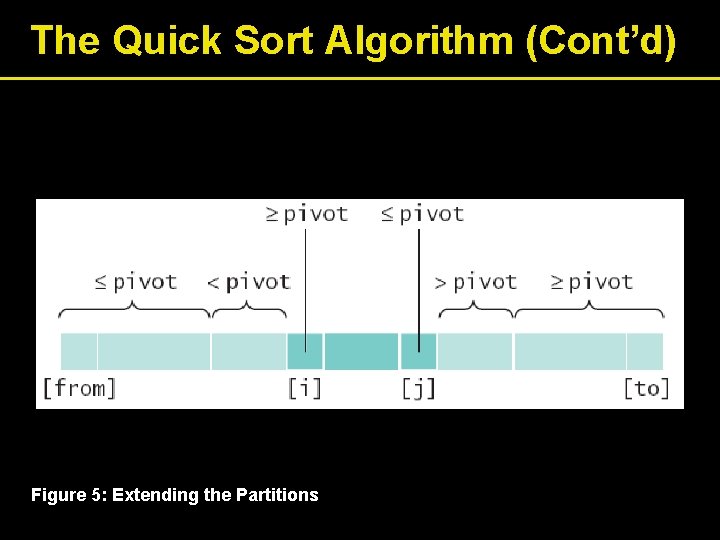
The Quick Sort Algorithm (Cont’d) Figure 5: Extending the Partitions

The Quick Sort Algorithm (Cont’d) • Quick Sort Steps 1. Select the pivot index = (L + R) / 2 2. Keep on the left partition all elements <= list[pivot] 3. Keep on the right partition all elements > list[pivot] list [0] [1] 6 2 L Pivot element 11 5 <= list[pivot] 3 1 -4 0 [9] -6 > list[pivot] -7 R Figure 6: Array list used with the quick sort algorithm
![The Quick Sort Algorithm (Cont’d) > list[pivot] <= list[pivot] list Pivot element [0] [1] The Quick Sort Algorithm (Cont’d) > list[pivot] <= list[pivot] list Pivot element [0] [1]](http://slidetodoc.com/presentation_image_h2/9595133027e1478180e0d8b4e0e10671/image-26.jpg)
The Quick Sort Algorithm (Cont’d) > list[pivot] <= list[pivot] list Pivot element [0] [1] -7 6 2 -6 11 5 0 3 LL L L 1 L [9] -4 0 5 -6 11 6 -7 R LR LL R R R Partition Point! Figure 6: Array list used with the quick sort algorithm

The Quick Sort Algorithm (Cont’d) private int partition(int from, int to) { int pivot = a[from]; int i = from - 1; int j = to + 1; while (i < j) { i++; while (a[i] < pivot) i++; j--; while (a[j] > pivot) j--; if (i < j) swap(i, j); } return j; }

Sorting Real Data • Arrays. sorts objects of classes that implement Comparable interface public interface Comparable { int compare. To(Object other. Object); } • The call a. compare. To(b) returns § A negative number is a should come before b § 0 if a and b are the same § A positive number otherwise

Sorting Real Data (Cont’d) • Several classes in Java (e. g. String and Date) implement Comparable • You can implement Comparable interface for your own classes public class Coin implements Comparable {. . . public int compare. To(Object other. Object) { Coin other = (Coin) other. Object; if (value < other. value) return -1; if (value == other. value) return 0; return 1; }. . . }
Sorting Real Data (Cont’d) • Once your class implements Comparable, simply use the Arrays. sort method: Coin[] coins = new Coin[n]; // Add coins. . . Arrays. sort(coins);
- Slides: 30