Sorting Algorithms Heaps and Merges COT 4810 Topics

Sorting Algorithms Heaps and Merges COT 4810 Topics in Computer Science Albert Park February 5, 2008

Sorting Algorithm n List and elements(or records) n Algorithm that puts elements of a list in a specific order n Increasing or decreasing n Numerical order n Efficient and optimize

Sorting Algorithm n The fastest n Heap and Merge sort n Time complexity n n O(n log n) Stable (Heap) vs. Unstable (Merge)

Heap Sort n Def: A sort algorithm that builds a heap, then repeatedly extracts the maximum item. n Complete tree n Proposed by J. Williams in 1964. n Implementation by Robert W. Floyd in 1964.

Heap Sort n Pseudocode Start at the beginning root node Set n = length of the list while n > 0 { swap (list[0], list[n-1]) while start > n { for node list[start] // usually start is the root node m = min(Child. A, Child. B) // find the minimum value of its child if list[start] > m then swap(list[start], list[m]) and start = m otherwise break out of while loop } n = n-1 }

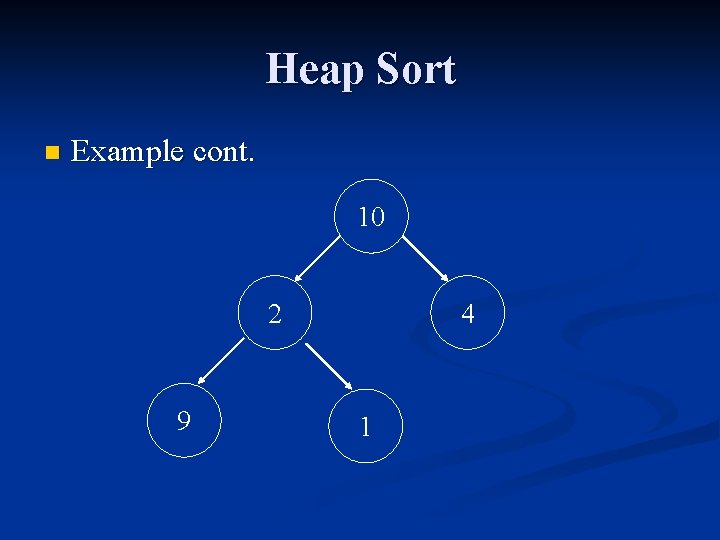
Heap Sort n Example 10 2 4 First construct a heap. Then sort the heap tree. 9 1

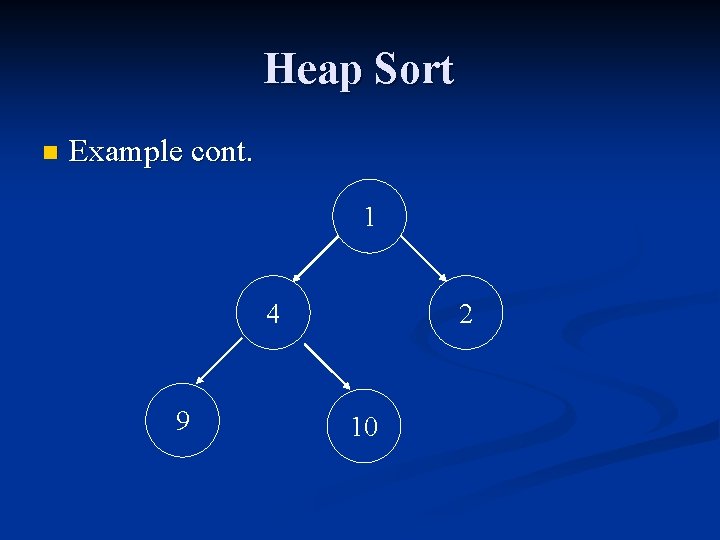
Heap Sort n Example cont. 10 2 9 4 1

Heap Sort n Example cont. 1 4 9 2 10

Merge Sort n Def: A sort algorithm that splits the items to be sorted into two groups, recursively sorts each group, and merges them into a final, sorted sequence. n Divide and Conquer n Memory

Merge Sort n Pseudocode sort(i, j): if i = j then return else k = (i+j)/2 sort(i, k) sort(k+1, j) merge A(i, k) and A(k+1, j) sort(1, n)

Merge Sort n Pseudocode merge: j= k = 1 for i = 1 to n if B(j) > C(k) then A(i) = B(j) and j = j+1 else A(i) = C(k) and k = k+1

Merge Sort n Example 10 Divide Conquer 2 4 9 1

Merge Sort 10 10 10 n 10 2 2 4 4 9 1 2 4 9 2 4 1 Example cont. 4 2 10 1 9

Merge Sort 2 n 4 10 1 2 Example cont. 1 4 9 9 10

Homework List 1 [3, 6, 4, 1, 5, 9, 2, 8] n 1. Sort the list above by using heapsort. n n 2. Sort the list above by using mergesort. n 3. What is the time complexity for both heap and merge sorts?

Work Sited Dewdney, A. K. The New Turing Omnibus. New York: Computer Science Press, 1989. n Belzer, Jack Encyclopedia of Computer Science and Technology. New York: Marcel Dekker, INC. , 1994. n Black, Paul E. "heapsort", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. , U. S. National Institute of Standards and Technology. 14 May 2007. n