Sorting Algorithm Overview n Sorting n Selection Sort

Sorting Algorithm

Overview n Sorting n Selection Sort n Code n Exchange/Bubble Sort Code n Insertion Sort n Code

Sorting n An array a is sorted (ascending order) if: for all i < j => a[i] a[j] n In the Real World: n Sorting is one of the most common operations in “data mining”

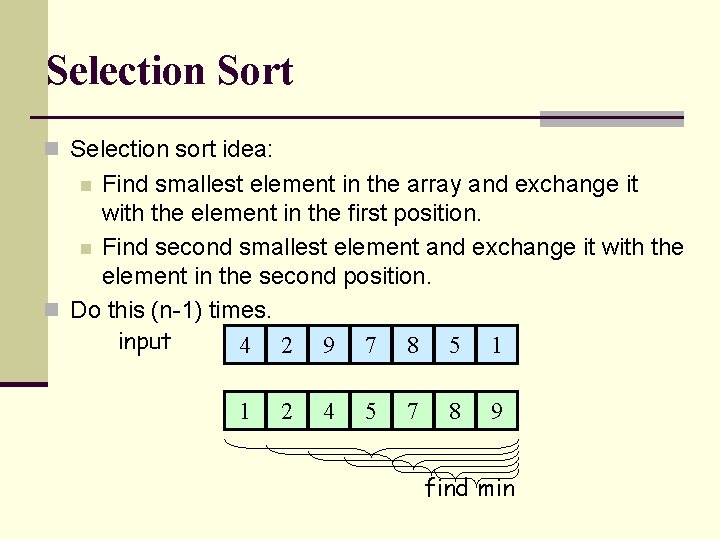
Selection Sort n Selection sort idea: Find smallest element in the array and exchange it with the element in the first position. n Find second smallest element and exchange it with the element in the second position. n Do this (n-1) times. input 4 2 9 7 8 5 1 n 14 2 49 75 78 875 491 find min

Selection sort void sel. Sort( int a[], int l) { for(i = 0 ; i < l ; i++) { min = i; for( j= i+1 ; j < l ; j++) { if( a[j] < a[min] ) min = j; } t = a[i]; a[i] = a[min] ; a[ min ] = t; }}

Improving Selection Sort • Selection sort finds minimum by linear search • Can we do better than this?

Exchange (“Bubble”) Sort n Bubble Sort Idea n Elements next to each other are swapped so that the list gets sorted 1. 2. Start with comparison of first two elements For ascending order, smaller value is placed before larger value § For descending order, smaller value is placed after larger value 3. 4. Continue until last two items are compared and evaluated for exchange When you can go through the list with no exchanges, the elements are sorted

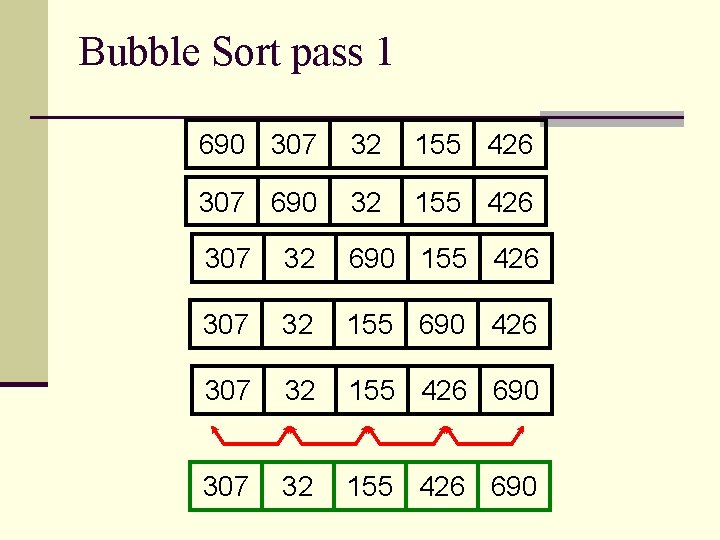
Bubble Sort pass 1 690 307 32 155 426 307 690 32 155 426 307 32 690 155 426 307 32 155 690 426 307 32 155 426 690

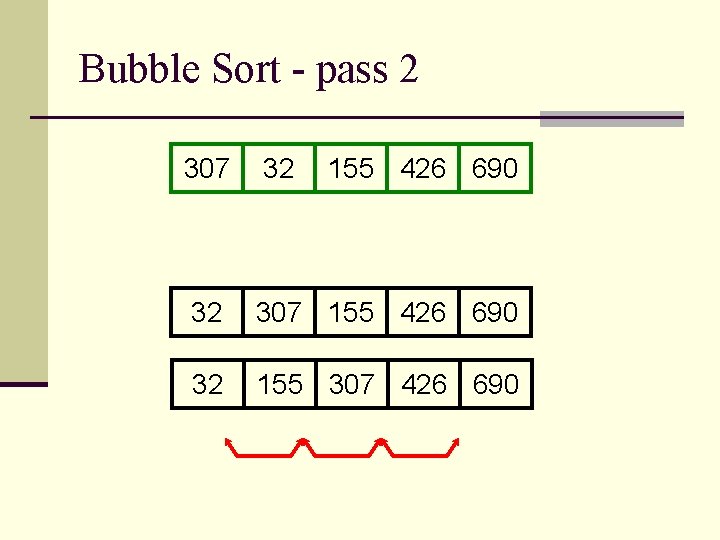
Bubble Sort - pass 2 307 32 155 426 690 32 307 155 426 690 32 155 307 426 690

Bubble Sort n Note that the largest value always sank to the bottom of list n The smaller elements slowly rose or “bubbled” up from the bottom n Each pass always places the largest in the list at the bottom n Hence, no need to do “compare and exchange” for the final two elements n For each pass, one less compare/exchange operation is required

Bubble Sort Code void bubble. Sort(int a[i] , int n) { for(p=0; p<=n-1; p++) // Loop for Pass { for(j=0; j<=n-1; j++) { if(a[j] > a[j+1]) { temp = a[j]; // Interchange Values a[j] = a[j+1]; a[j+1] = temp; } }

Insertion Sort n Idea: like sorting a hand of playing cards n Start with an empty left hand the cards facing down on the table. n Remove one card at a time from the table, and insert it into the correct position in the left hand n n compare it with each of the cards already in the hand, from right to left The cards held in the left hand are sorted n these cards were originally the top cards of the pile on the table 13

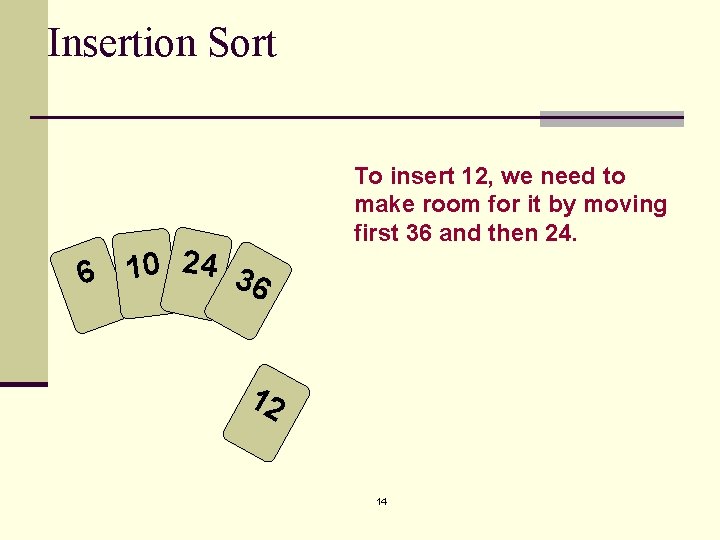
Insertion Sort 6 10 24 36 To insert 12, we need to make room for it by moving first 36 and then 24. 12 14

Insertion Sort 6 10 24 36 12 15

Insertion Sort 6 10 24 3 6 12 16

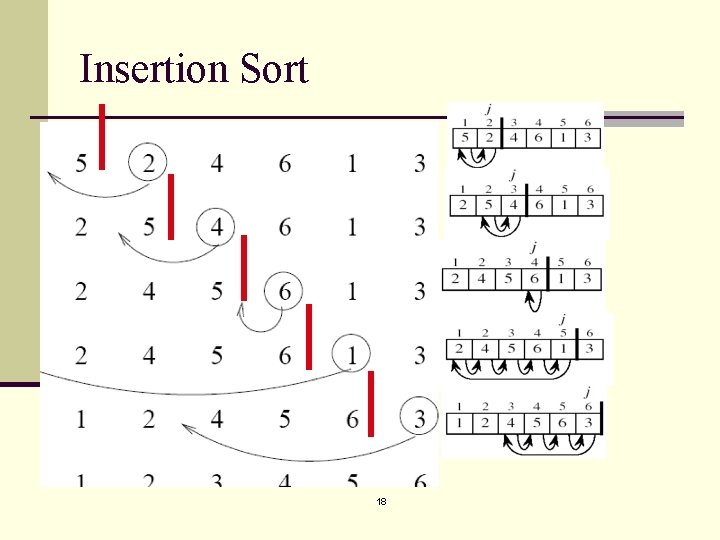
Insertion Sort input array 5 2 4 6 1 3 at each iteration, the array is divided in two sub-arrays: left sub-array right sub-array unsorted 17

Insertion Sort 18

Insertion sort 19

Insertion Sort Algorithm int a[6] = {5, 1, 6, 2, 4, 3}; int i, j, key; for(i=0; i<6; i++) { key = a[i]; j = i-1; while(j>=0 && key < a[j]) { a[j+1] = a[j]; j--; } a[j+1] = key; } 20