Sorting Algorithm Analysis Sorting Sorting is important Things

Sorting Algorithm Analysis

Sorting ® Sorting is important! ® Things that would be much more difficult without sorting: – finding a phone number in the phone book – looking up a word in the dictionary – finding a book in the library – buying a cd/dvd – renting a video – buying groceries ® Any more ideas? ? ?

How to sort? ® Sorting the student roster: Alex Guttler Matt Simon Alexandra Eurdolian Katie Blaszak Joseph Kelly An Xuan Rebecca Davis ® Sorting a hand of cards

Comparison-based sorting ® Ordering decision based on comparison of elements ® Requires that elements are comparable – have a natural order • numerical § numbers • lexicographic (alphabetical) § characters • chronological § dates

Arrays ® Used to store a collection or list of elements of the same type ® Arrays are indexed ® Example: an array A of integers A= ® 4 8 4 1 9 6 7 0 1 2 3 4 5 is the element of the array at index 1 ® A[1]=4 array elements array indices

Insertion Sort ® Similar to sorting a hand of cards ® Good for sorting a small number of elements ® Idea: – n is number of elements or input size – start at element A[0] • already sorted – for k = 1, 2, …, n sort elements A[0] through A[k] by comparing A[k] with each element A[k-1], A[k-2], …, A[1], A[0]

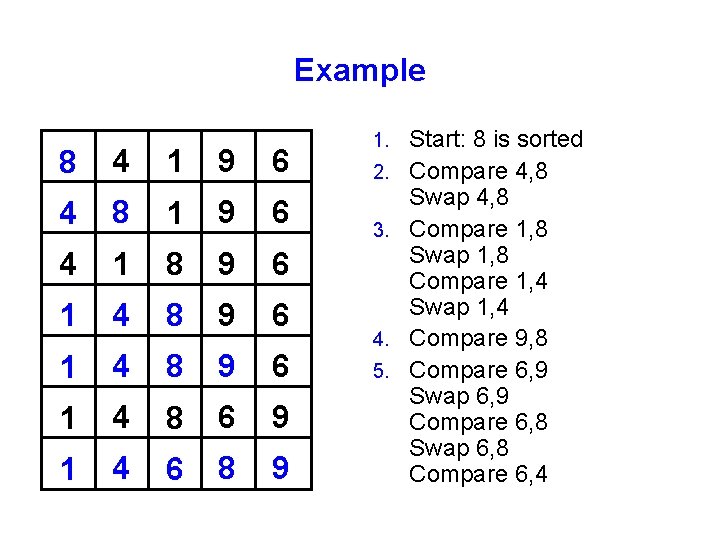
Example 8 4 1 9 6 4 8 1 9 6 4 1 8 9 6 1 4 8 6 9 1 4 6 8 9 1. 2. 3. 4. 5. Start: 8 is sorted Compare 4, 8 Swap 4, 8 Compare 1, 8 Swap 1, 8 Compare 1, 4 Swap 1, 4 Compare 9, 8 Compare 6, 9 Swap 6, 9 Compare 6, 8 Swap 6, 8 Compare 6, 4

Algorithm analysis Determine the amount of resources an algorithm requires to run – computation time, space in memory ® Running time of an algorithm is the number of basic operations performed – additions, multiplications, comparisons – usually grows with the size of the input – faster to add 2 numbers than to add 2, 000! ® Example: Adding n numbers takes linear time – requires n – 1 basic operations (additions) – number of basic operations is proportional to the size of the input ®

Running times ® Worst-case running time – upper bound on the running time – guarantee the algorithm will never take longer to run ® Average-case running time – time it takes the algorithm to run on average (expected value) ® Best-case running time – lower bound on the running time – guarantee the algorithm will not run faster

Analysis of Insertion Sort ® We compare each element with previous elements until the ordering is correct ® In the worst case, we compare each element with all of the previous elements – A[1] is compared with A[0] – A[2] is compared with A[1], A[0] – A[3] is compared with A[2], A[1], A[0] – A[4] is compared with A[3], A[2], A[1], A[0] … – A[n-1] is compared with A[n-2], …, A[1], A[0]

Number of comparisons (worst case) ® Element k requires k comparisons ® Total number of comparisons: 0+1+2+ … + n-1 = ½ (n)(n-1) = ½ (n 2 -n) ® Running time of insertion sort in the worst case is quadratic ® Worst case behavior occurs when the array is in reverse sorted order 9 8 7 6 4 1

Number of comparisons (best case) ® What if the array is already sorted? 1 ® How 4 6 7 8 9 many comparisons per element will be made by insertion sort?

Running time of Insertion Sort ® Best case running time is linear ® Worst case running time is quadratic ® Average case running time is quadratic ® Insertion sort is only practical for small input – 100 operations to sort 10 elements – 10000 operations to sort 100 elements – 1000000 operations to sort 1000 elements ® There are more efficient sorting algorithms!

The divide-and-conquer approach ® Insertion sort uses an incremental approach – puts elements in correct place one at a time ® We can design more efficient sorting algorithms using the divide-and-conquer approach: – Divide the problem into a number of subproblems – Conquer the subproblems by solving them recursively until the subproblems are small enough to solve directly – Merge the solutions for the subproblems into the solution for the original problem

Mergesort ® Divide-and-conquer ® Given sorting algorithm an array of n elements – Divide the array into two subarrays each with n/2 items – Conquer (solve) each subarray by sorting it recursively – Merge the solutions to the subarrays by merging them into a single sorted array

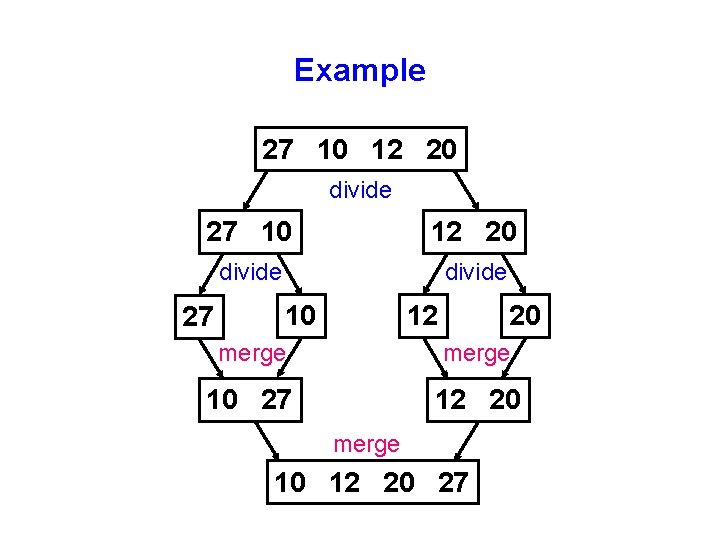
Example 27 10 12 20 divide 27 10 12 20 merge 10 27 12 20 merge 10 12 20 27

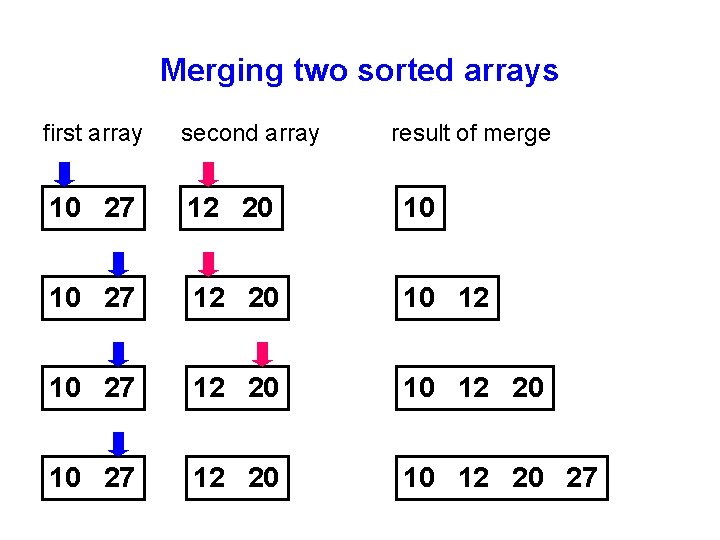
Merging two sorted arrays first array second array result of merge 10 27 12 20 10 12 20 27