SOOSTRC WRF Environmental Modeling System Simulated Radar Reflectivity

SOO/STRC WRF Environmental Modeling System Simulated Radar Reflectivity Robert Rozumalski National SOO Science and Training Resource Coordinator NOAA/NWS/OCWWS/Training Division/FDTB

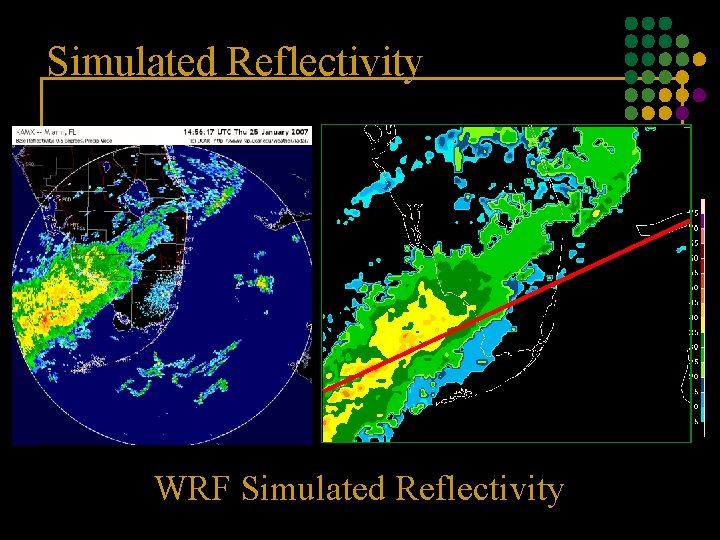
Simulated Reflectivity WRF Simulated Reflectivity

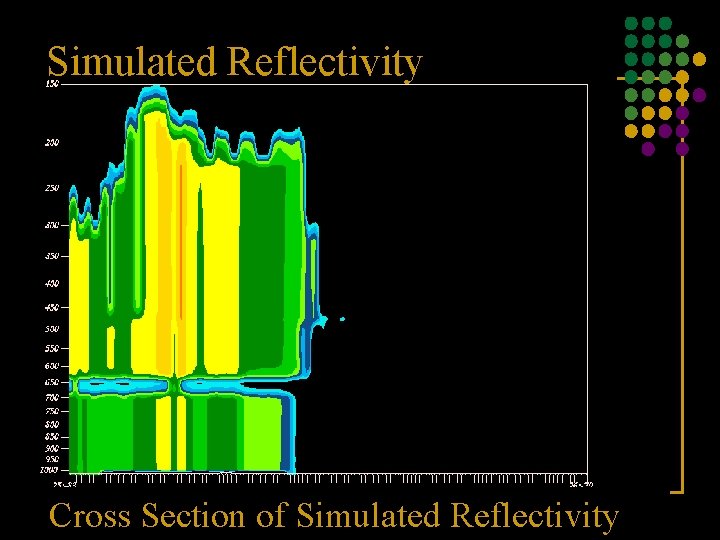
Simulated Reflectivity Cross Section of Simulated Reflectivity

Simulated Reflectivity

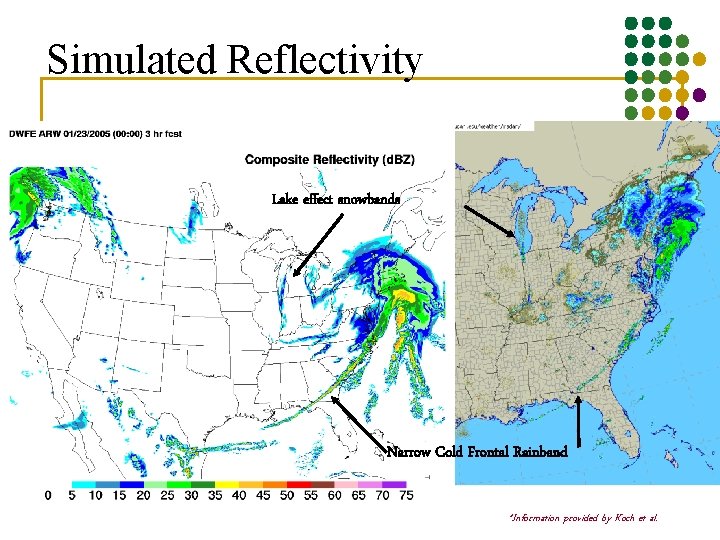
Simulated Reflectivity Lake effect snowbands Narrow Cold Frontal Rainband *Information provided by Koch et al.

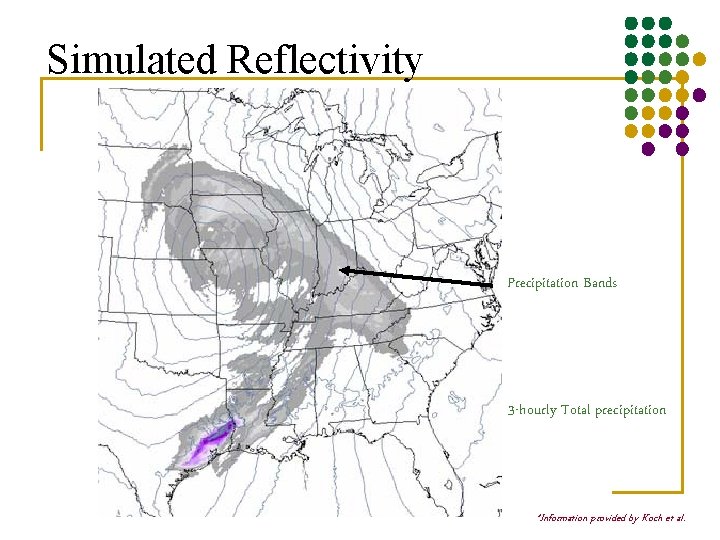
Simulated Reflectivity Precipitation Bands 3 -hourly Total precipitation *Information provided by Koch et al.

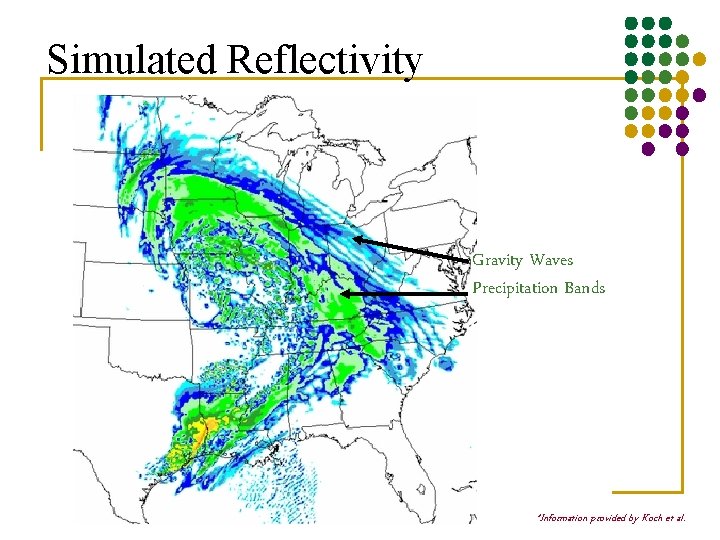
Simulated Reflectivity Gravity Waves Precipitation Bands *Information provided by Koch et al.

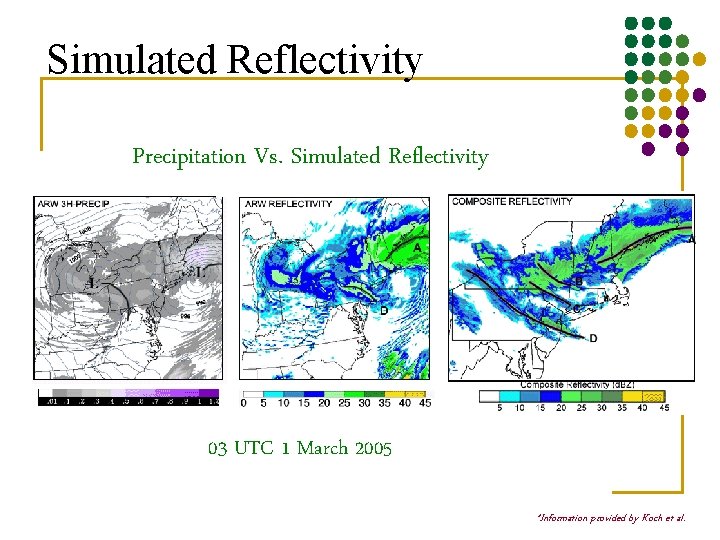
Simulated Reflectivity Precipitation Vs. Simulated Reflectivity 03 UTC 1 March 2005 *Information provided by Koch et al.

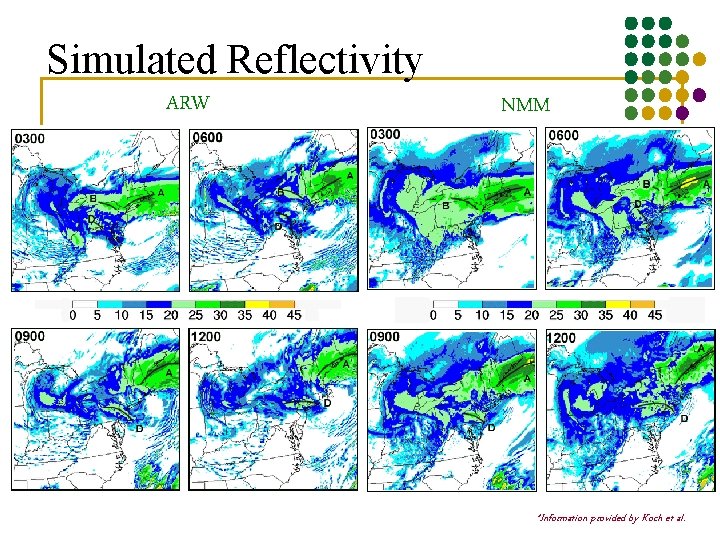
Simulated Reflectivity ARW NMM *Information provided by Koch et al.

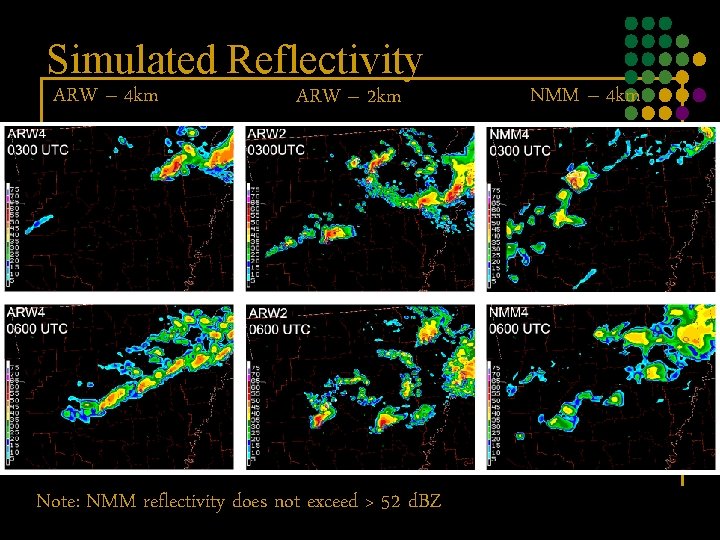
Simulated Reflectivity ARW – 4 km ARW – 2 km Note: NMM reflectivity does not exceed > 52 d. BZ NMM – 4 km

Simulated Reflectivity Simulated reflectivity offers several advantages over customary accumulated precipitation products • • Easier to visualize relationships between cloud and precipitation bands Many mesoscale phenomena are more readily revealed, especially during the cold season Convective storm structures, such as supercells, are more clearly identified Possibility of drawing comparisons to observed radar imagery for model verification *Information provided by Koch et al.

Simulated Reflectivity Simulated reflectivity – Caveat Emptor! • • One can not draw conclusions about the relative performance of NWP models unless the reflectivity is computed such that it is consistent with model microphysics It is not possible to make strict comparisons between predicted vertical profiles of reflectivity and observed radar imagery because: v v Radar resolution degrades with distance from transmitter Information is lost at low levels due to earth curvature Ground clutter, AP, and other issues Bright Banding *Information provided by Koch et al.

SOO/STRC WRF Environmental Modeling System Simulated Radar Reflectivity The End

Simulated Reflectivity The difference in the reflectivity product appearance between the WRF-NMM and ARW models is largely attributed to the differences in model microphysics -primarily the snow intercept parameter and the size distributions for snow *Information provided by Koch et al.

Simulated Reflectivity Both cores use single-moment microphysics schemes that assume the Marshall. Palmer exponential DSD: Ns(Ds) = Nosexp(-ls. Ds) Where: Ns(Ds) = The number of snow particles per unit size range per unit volume Nos = Snow intercept parameter Ds = The diameter of the snow particles ls = The slope factor for snow Equivalent reflectivity is computed using the S(ND 6) method assuming Rayleigh scattering and spherical hydrometeors *Information provided by Koch et al.

Simulated Reflectivity • ARW Core Microphysics v. WSM 5 – 5 class scheme v. WSM 6 – 6 class scheme (WSM 5 + graupel) • In WRF Postprocessor v. Cloud water and ice are combined v. Rain and snow are also combined v. Fixed intercept No used in computing reflectivity even though WSM 5/6 uses a temperature dependent No *Information provided by Koch et al.

Simulated Reflectivity • NMM Core Microphysics (Ferrier) has 4 classes of hydrometeors v Cloud liquid v Cloud Ice v Mixed Ice (Snow, v Rain graupel, sleet) • In WRF Postprocessor uses same temperature dependent No, which is consistent with Ferrier scheme *Information provided by Koch et al.

Simulated Reflectivity Method for computing simulated reflectivity Equivalent reflectivity factor for M-P distribution Ze = G(7)Nol-7 After accounting for non-solid ice particles and the larger dielectric constant for liquid compared to ice (Kl/Ki) = 5. 3: Ze = 0. 224 G(7)Nol-7(rs/ri)2 The slope factor for snow (l) depends on the snow mixing ratio l = ((p. Nors)/(raqs))1/4 *Information provided by Koch et al.

Simulated Reflectivity Method for computing simulated reflectivity It can be shown that the equivalent reflectivity factor for snow can be written in terms of the snow mass content Ms and the snow number concentration ns instead of the slope factor and intercept parameter as follows: Ze = 1. 634 x 104 (Ms 2/ns) Thus, for the same snow mass content, differences in radar reflectivity will scale with differences in parameterized snow number concentrations; e. g. , for a value of ns = 0. 1 g m-3: d. BZe. S=31. 1+17. 5 log. MS = 13. 6 - Fixed intercept ARW d. BZe. S=38. 6+17. 5 log. MS = 21. 1 - WSM-5 d. BZe. S=30. 0+10 log. MS = 20. 0 - NMM Ferrier *Information provided by Koch et al.

Simulated Reflectivity Method for computing simulated reflectivity The Ferrier (NMM) method predicts higher reflectivity values than the Fixed-intercept (ARW) method for all values of snow number concentrations ns < 0. 713 gm-3 For convective storms, the NMM reflectivity values are restricted to a value of 52 d. BZ, which is primarily the result of the following imposed restrictions: v. The mean size of raindrops is assumed fixed at 0. 45 mm for rain contents > 1 gm -3 v. The maximum number concentration of precipitating ice is fixed, and thus the intercept parameter is fixed *Information provided by Koch et al.