Sommaire Calculs simples Distributivit simple Distributivit double explication

Sommaire Calculs simples Distributivité simple Distributivité double (explication) Distributivité double (exercices) Deux difficultés classiques Exercices sur la distributivité Exercices variés

CALCULS SIMPLES Savoir additionner et soustraire les nombres relatifs 3 + 7 = 10 3 - 7 = - 4 - 3 + 7 = 4 - 3 - 7 = -10 Savoir multiplier les nombres relatifs 3 × 7 = 21 3 × (- 7) = - 21 (- 3) × 7 = - 21 (- 3) × (- 7) = 21 Connaître les formules a(b + c) = ab + ac a(b - c) = ab - ac

DISTRIBUTIVITE SIMPLE (5ème) Développer 3(x + 2)= 3 × x + 3 × 2 = 3 x + 6 5(2 x - 3)= 10 x - 15 calcule mentalement 5 × 2 x et 5 × 3 Maintenant attention aux signes!!! 3(2 x - 4) + 3(4 x - 8) = 6 x - 12 + 12 x - 24 = 18 x - 36 3(2 x + 4) + 3(4 x - 8) = 6 x + 12 x - 24 = 18 x - 12 3(2 x - 4) - 3(4 x - 8) = 6 x - 12 x + 24 attention -3 × (-8) = +24 = - 6 x + 12 6 x -12 x = - 6 x 3(2 x - 4) - 3(4 x + 8) = 6 x - 12 x - 24 = - 6 x - 36 -3(2 x - 4) - 3(4 x - 8) = - 6 x + 12 - 12 x + 24 = - 18 x + 36

DISTRIBUTIVITE DOUBLE Pour développer le produit (3 x - 2)(4 x - 3) Tu dois penser (3 x - 2) × (4 x - 3) = 3 x × 4 x + 3 x × (-3) + (-2 ) × 4 x + (-2) × (-3) Et calculer mentalement 3 x × 4 x ; 3 x × (-3) ; (- 2) × 4 x ; (-2) × (-3) 12 x² -9 x -8 x Pour marquer directement (sans écrire ce que tu penses) (3 x - 2)(4 x - 3) = 12 x² - 9 x - 8 x + 6 = 12 x² - 17 x +6 +6

DISTRIBUTIVITE DOUBLE (2 x + 3)(3 x + 5) = (2 x + 3)(3 x - 5) = (2 x - 3)(3 x + 5) = (2 x - 3)(3 x - 5) = Ne pas confondre avec 2 x + 3(3 x + 5)= Il faut aussi savoir développer, réduire et ordonner (4 x - 1)(2 x - 5) + (2 x - 1)(3 x + 2) = Bien lire l’énoncé (4 x - 1)(2 x - 5) + 2 x - 2(3 x + 2) =

DISTRIBUTIVITE DOUBLE (2 x + 3)(3 x + 5) = 6 x² + 10 x + 9 x + 15 = 6 x² + 19 x + 15 (2 x + 3)(3 x - 5) = 6 x² - 10 x + 9 x - 15 = 6 x² - x - 15 (2 x -3)(3 x + 5) = 6 x² + 10 x - 9 x - 15 = 6 x² + x - 15 (2 x-3)(3 x-5) = 6 x² - 10 x - 9 x + 15 = 6 x² - 19 x + 15 Ne pas confondre avec 2 x + 3(3 x + 5) = 2 x + 9 x + 15 = 11 x + 15

Il faut aussi savoir développer, réduire et ordonner (4 x -1)(2 x - 5) + (2 x - 1)(3 x+ 2) = 8 x² - 20 x - 2 x + 5 + 6 x² + 4 x -3 x - 2 = 14 x²- 21 x+ 3 Bien lire l’énoncé (4 x - 1)(2 x - 5) + 2 x - 2(3 x + 2) = 8 x² - 20 x - 2 x + 5 + 2 x - 6 x - 4 = 8 x²- 26 x + 1

DEUX DIFFICULTES CLASSIQUES 1) Le signe - placé devant un produit ( 3 x+2 )( 4 x - 5 ) -[ ( x + 3 )( 2 x - 5) ] On ajoute des crochets = 12 x² - 15 x + 8 x - 10 - [ 2 x² - 5 x + 6 x -15 ] On multiplie par « -1 » = 12 x² - 15 x + 8 x - 10 - 1 × [ 2 x² - 5 x + 6 x -15 ] = 12 x² - 15 x + 8 x - 10 - 2 x² + 5 x - 6 x +15 = 10 x² - 8 x +5 A ton tour 4 x² - ( 3 x + 2 ) ( 2 x - 1 ) = -2 x² - x + 2

DEUX DIFFICULTES CLASSIQUES 2) Le produit de trois facteurs ( 4 x + 2 )( 4 x - 1 ) + 3 [( x + 3 )( 2 x - 5)] On ajoute des crochets = 16 x² - 4 x + 8 x - 2 + 3 [ 2 x² - 5 x + 6 x -15 ] = 16 x² - 4 x + 8 x - 2 + 6 x² - 15 x + 18 x - 45 = 22 x² + 7 x - 47 A ton tour : 4 x² -2 ( 3 x + 2 ) ( 2 x - 1 ) = -8 x² -2 x + 4

Quelques exercices Développe, réduis et ordonne les expressions suivantes

Développe, réduis et ordonne les expressions suivantes: A=(4 x+2)(3 x+4) = 12 x² + 22 x + 8 = 10 x² - 11 x + 3 B=(5 x-3)(2 x-1) = 3 a² + 5 a - 12 C=(3 a-4)(a+3) D=(5 a+5)(2 a-1) = 10 a² + 5 a - 5 E=(2 x-3)(4 x-1)+2(3 x-2)(4 x-5) = 32 x² - 60 x + 23 G=(2 x-1)(2 x-2)+(x-2)(x-5) = 5 x² -13 x + 12 A=(3 x+5)(5 x+2) = 15 x² + 31 x + 10 B=(5 x-2)(5 x+3) = 25 x² + 5 x - 6 C=(3 a-5)(2 a-1) = 6 a² - 13 a + 5 D=(5 a+7)(a-3) = 5 a² - 8 a - 21 E=(2 x-3)(4 x-2)-(3 x-1)(4 x-5) = -4 x² + 3 x + 1 G=(2 x-3)(x-2)+(x-3)(x-1) = 3 x² -11 x + 9

* Exprime l'aire A A = (x + 7)(x - 3) et le périmètre P P = 4 x + 8 du rectangle ci-contre x -3 en fonction de x. (x > 3). x+7 Calcule cette aire et ce périmètre si x = 13/3 A = 136/9 P = 76/3 * Traduire les 5 premières consignes par un calcul littéral Et trouve la consigne manquante. . Soit a un nombre. a+3. Ajouter 3. . Prendre le double du résultat (a + 3) × 2= 2(a + 3) = 2 a + 6. Multiplier le nouveau résultat par 3 (2 a + 6) × 3 = 6 a + 18 retrancher 18. 6 a + 18 -18 = 6 a. Divise le résultat obtenu par 6. Pour retrouver le nombre a

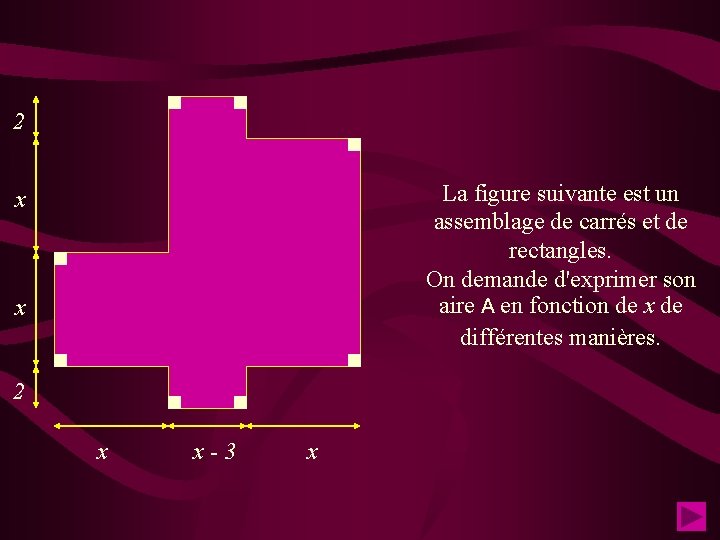
2 La figure suivante est un assemblage de carrés et de rectangles. On demande d'exprimer son aire A en fonction de x de différentes manières. x x 2 x x-3 x

Traduis ce découpage par une expression littérale. Développe et réduis cette expression. 2 2(x-3) x x(x-3) x² x x² 2(x-3) 2 x x-3 x A = 3 x² + 2 x(x - 3) + 4(x-3) = 3 x² + 2 x² - 6 x + 4 x - 12 = 5 x² - 2 x - 12

2 2(x-3) x x(x - 3 + x) x x(x + x - 3 + x) Traduis ce découpage par une expression littérale. Développe et réduis cette expression. 2(x-3) 2 x x-3 x A = x(x + x - 3 + x) + x(x + x - 3) + 4(x - 3) = x² + x² - 3 x + x² -3 x + 4 x - 12 = 5 x² - 2 x - 12

2 (2 x + x 3) x² 4)(x - x 2 x² Traduis ce découpage par une expression littérale. Développe et réduis cette expression. 2 x x-3 x A = x² + (2 x + 4)(x - 3) + 2 x² = x² + 2 x² - 6 x + 4 x² - 12 + 2 x² = 5 x² - 2 x - 12

Calcule A = (2 x + 4)(3 x - 3) - 6 x -x(x + 2) 2 x Quel découpage faut - il imaginer pour trouver cette expression ? x 2 x x-3 x A = (2 x + 4)(3 x - 3) - 6 x -x(x + 2) = 6 x² - 6 x + 12 x - 12 - 6 x -x² - 2 x = 5 x² - 2 x -12

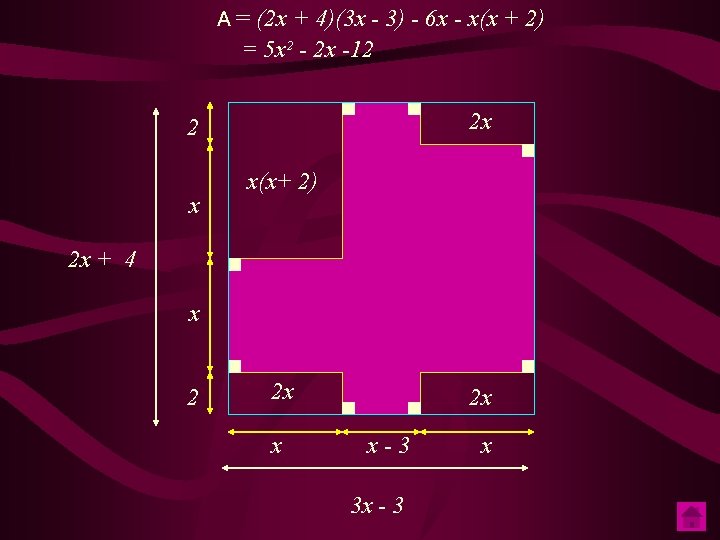
A = (2 x + 4)(3 x - 3) - 6 x - x(x + 2) = 5 x² - 2 x -12 2 x 2 x x(x+ 2) 2 x + 4 x 2 2 x x-3 3 x - 3 x