Some places where Special Relativity is needed Particle









- Slides: 20

Some places where Special Relativity is needed Particle accelerator: electrons and positrons moving at 99. 99% c Supernova in a distant galaxy. Remember the universe is expanding ! GPS satellite in orbit (v~3. 9 km/sec, 7μs/day SR correction) Copyright © 2012 Pearson Education Inc.

Review from Friday: Einstein’s postulates • Einstein’s first postulate: The laws of physics are the same in all inertial reference frames • Einstein’s second postulate is that the speed of light in vacuum is the same in all inertial frames of reference and is independent of the motion of the source. • We must modify determination of space and time intervals when a frame of reference is moving relative to us at high velocity. (Today’s class: tough deep material, please slow me down if I start going too fast. Reread the textbook when you go home). • Another consequence: it is impossible for an inertial observer to travel at c, the speed of light in the vacuum. Copyright © 2012 Pearson Education Inc.

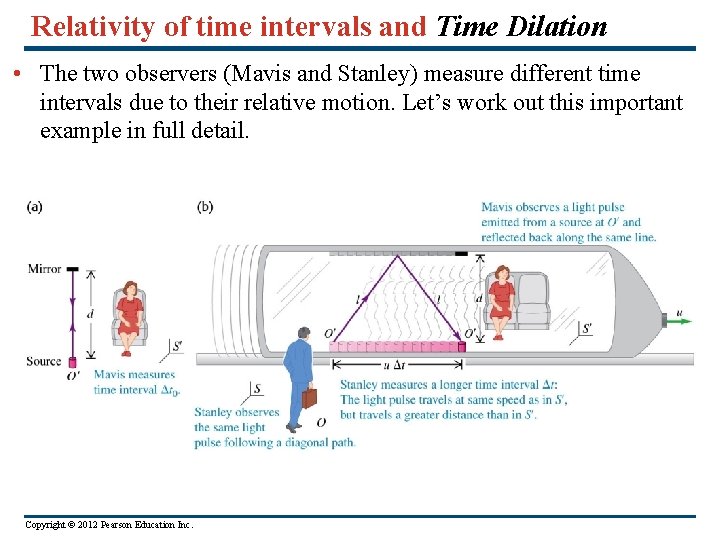
Relativity of time intervals and Time Dilation • The two observers (Mavis and Stanley) measure different time intervals due to their relative motion. Let’s work out this important example in full detail. Copyright © 2012 Pearson Education Inc.

Relativity of time intervals and Time Dilation • The two observers (Mavis and Stanley) measure different time intervals due to their relative motion. Let’s work out this example. Mavis in reference frame S’ fires a light source at a mirror and measures the time interval. What does she find ? This is a “proper time interval” – a time interval between events at the same space point. Copyright © 2012 Pearson Education Inc.

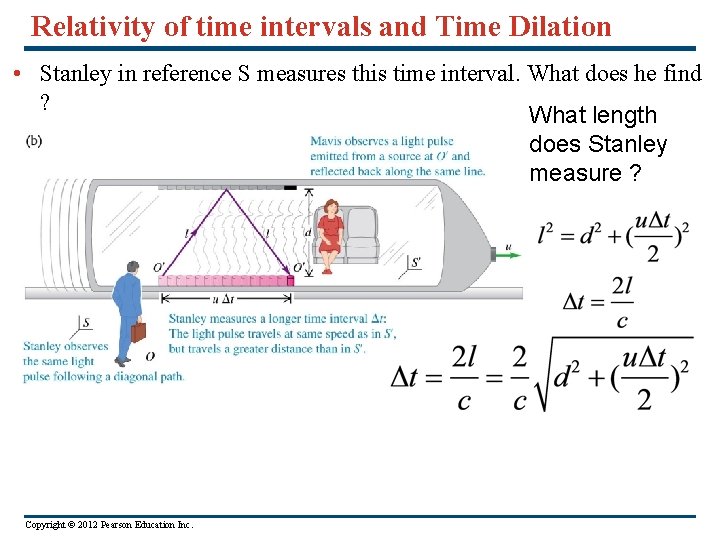
Relativity of time intervals and Time Dilation • Stanley in reference S measures this time interval. What does he find ? What length does Stanley measure ? Copyright © 2012 Pearson Education Inc.

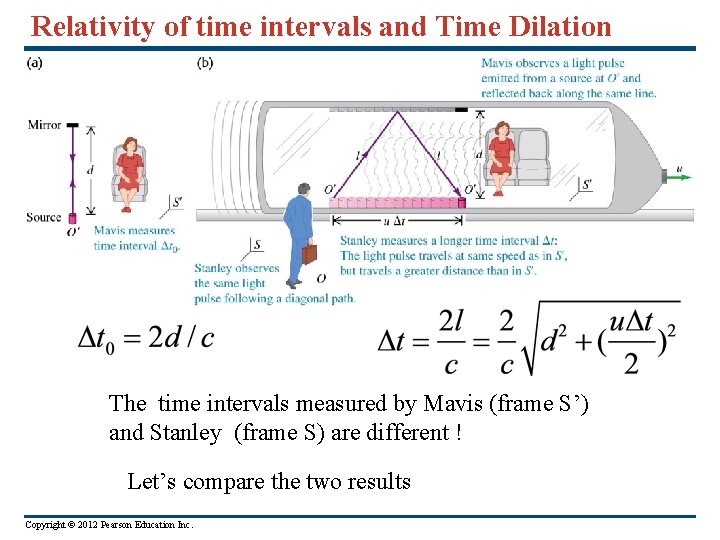
Relativity of time intervals and Time Dilation The time intervals measured by Mavis (frame S’) and Stanley (frame S) are different ! Let’s compare the two results Copyright © 2012 Pearson Education Inc.

Relativity of time intervals and Time Dilation The time intervals measured by Mavis (frame S’) and Stanley (frame S) are different ! Let’s work out how they are related. Now square this and collect Δt terms Copyright © 2012 Pearson Education Inc.

Relativity of time intervals and Time Dilation Question: does Stanley measure a longer or shorter time interval ? Stanley measures a longer round trip time than Mavis ! This is called relativistic time dilation Copyright © 2012 Pearson Education Inc.

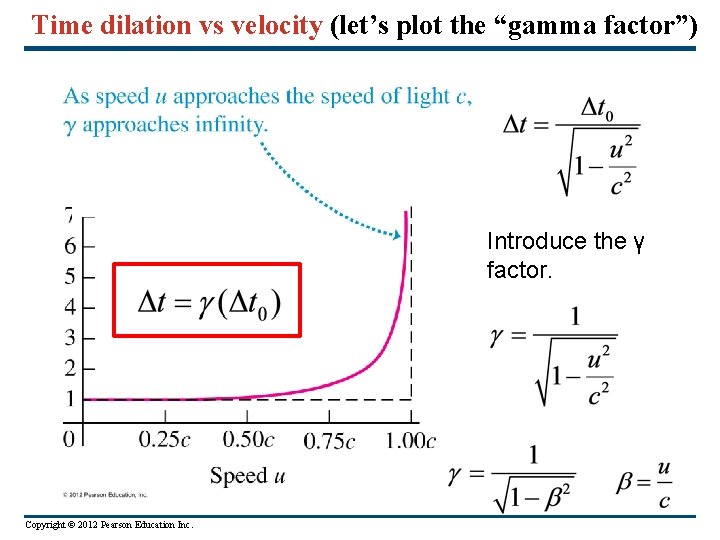
Time dilation vs velocity (let’s plot the “gamma factor”) Introduce the γ factor. Copyright © 2012 Pearson Education Inc.

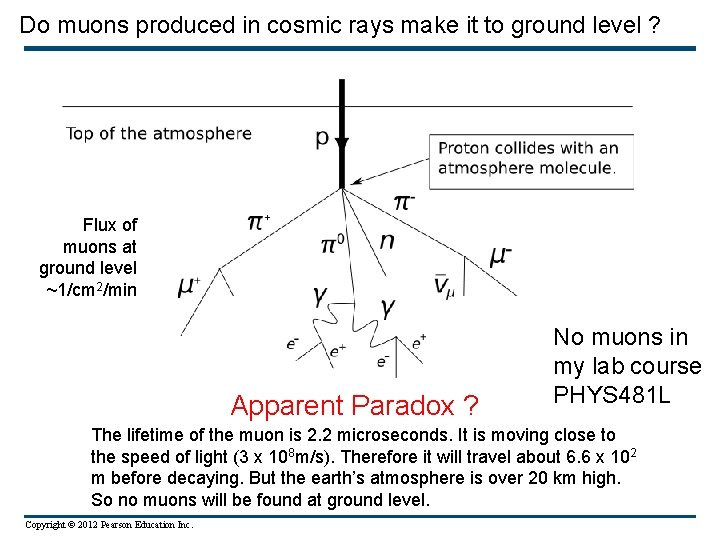
Do muons produced in cosmic rays make it to ground level ? Flux of muons at ground level ~1/cm 2/min Apparent Paradox ? No muons in my lab course PHYS 481 L The lifetime of the muon is 2. 2 microseconds. It is moving close to the speed of light (3 x 108 m/s). Therefore it will travel about 6. 6 x 102 m before decaying. But the earth’s atmosphere is over 20 km high. So no muons will be found at ground level. Copyright © 2012 Pearson Education Inc.

Time dilation example A muon decays into other particles with a mean lifetime of 2. 20 μs = 2. 20 x 10 -6 sec as measured in a reference frame in which it is at rest. If a muon is moving at 0. 990 c relative to the earth, what will an observer on earth measure its mean lifetime to be ? Reference frame S’ of the muon, proper lifetime Δt 0= 2. 20 μs Reference frame S of the earth; relative speed of S’ and S is u=0. 990 c Question: What is the gamma factor here ? Copyright © 2012 Pearson Education Inc. 7. 1 !

Another time dilation example Mavis boards a spaceship and zips past Stanley on earth at a relative speed of 0. 600 c. At the instant she passes him both start timers. a) A short time later Stanley measures that Mavis has traveled 9. 00 x 107 m and is passing a space station. What does Stanley’s timer read as she passes the station ? What does Mavis’ timer read ? Reference frame S of Stanley; reference frame S’ of Mavis, speed of S’ relative to S is u=0. 600 c In S, Mavis passes at 0. 600 c = 1. 80 x 108 m/s and covers the distance in 9. 00 x 107 m/1. 80 x 108 m/s= 0. 500 s Mavis is measuring proper time Copyright © 2012 Pearson Education Inc.

Twin Paradox Eartha and Astrid are twins. Eartha remains on Earth while Astrid travels at relativistic velocities throughout the galaxy. According to Eartha, Astrid’s heartbeat and life processes are proceeding more slowly than her own. When Astrid returns to Earth, she will be younger than Eartha. But can’t Astrid make the same argument ? Resolution: the situation is not symmetric. Astrid had to accelerate to attain relativistic velocities. Astrid is not in an inertial reference frame. Copyright © 2012 Pearson Education Inc.

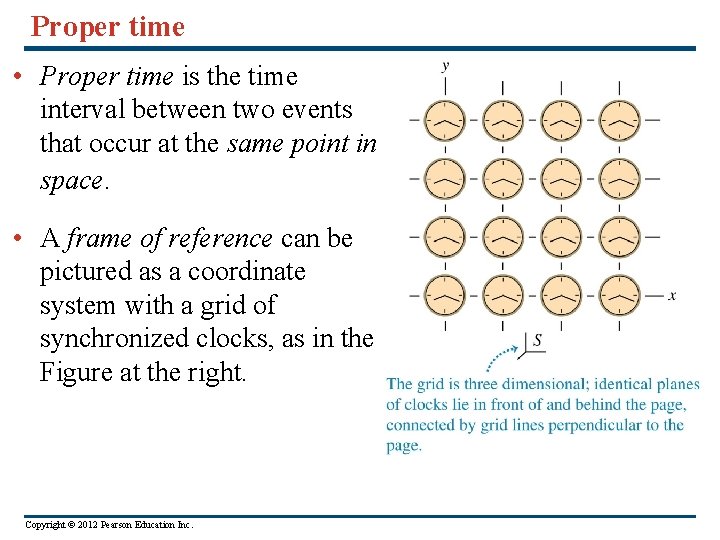
Proper time • Proper time is the time interval between two events that occur at the same point in space. • A frame of reference can be pictured as a coordinate system with a grid of synchronized clocks, as in the Figure at the right. Copyright © 2012 Pearson Education Inc.

Relativity of length Copyright © 2012 Pearson Education Inc.

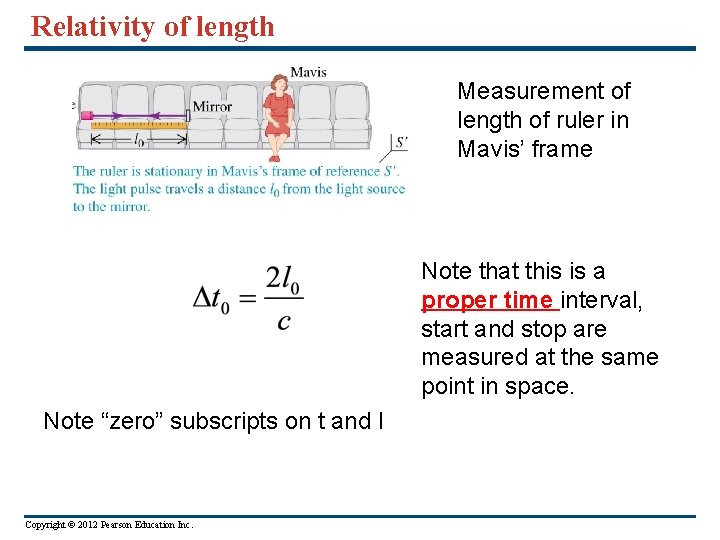
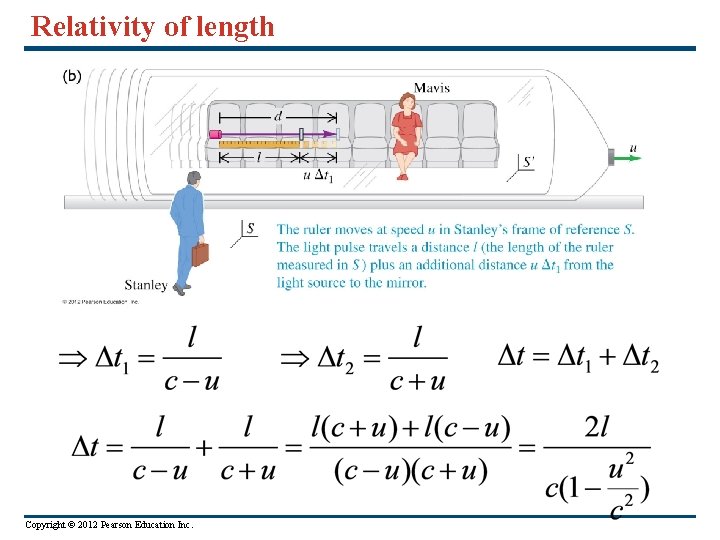
Relativity of length Measurement of length of ruler in Mavis’ frame Note that this is a proper time interval, start and stop are measured at the same point in space. Note “zero” subscripts on t and l Copyright © 2012 Pearson Education Inc.

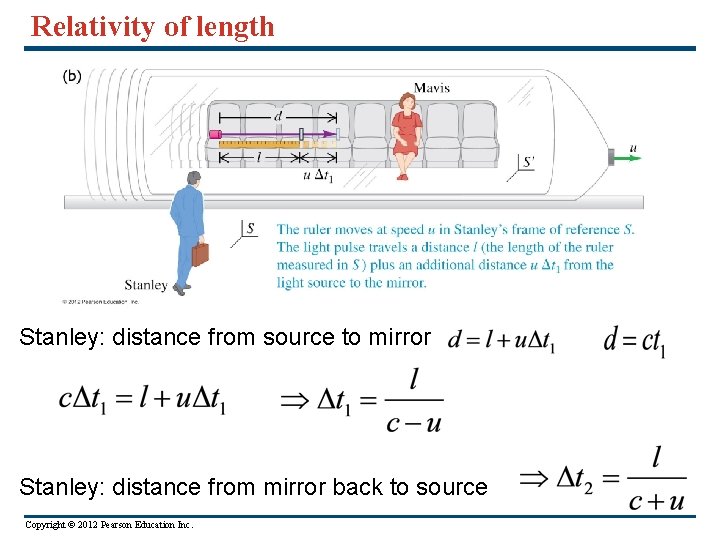
Relativity of length Stanley: distance from source to mirror Stanley: distance from mirror back to source Copyright © 2012 Pearson Education Inc.

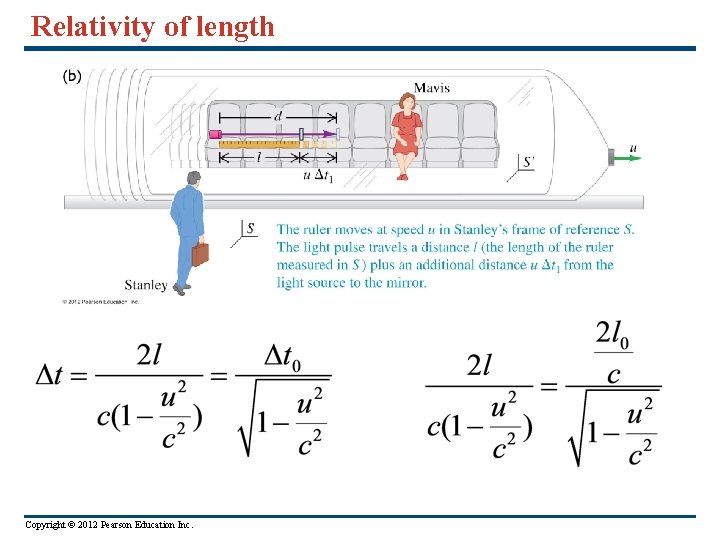
Relativity of length Copyright © 2012 Pearson Education Inc.

Relativity of length Copyright © 2012 Pearson Education Inc.

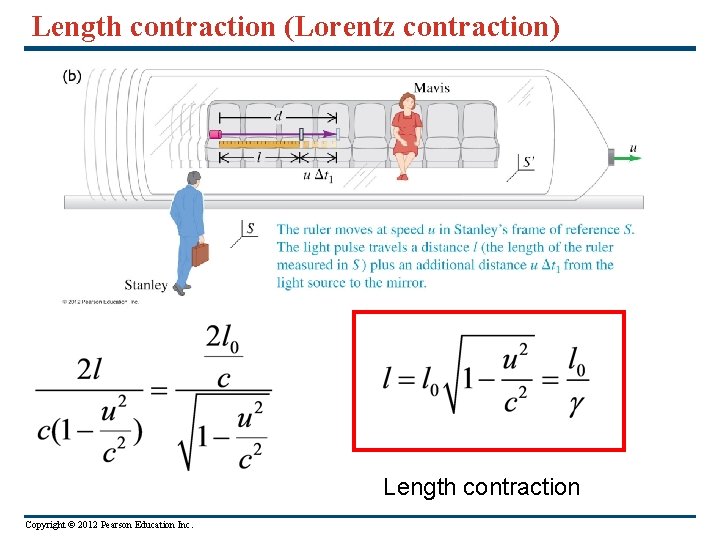
Length contraction (Lorentz contraction) Length contraction Copyright © 2012 Pearson Education Inc.