Some Fundamentals of Doppler Radar Velocity Analysis L

Some Fundamentals of Doppler Radar Velocity Analysis L. Jay Miller (August 2011) Using the CEDRIC program for wind synthesis and other analyses

Acknowledgements of Support Administrative and logistics – Tammy Kepple, Robert Rilling, and Phillip Stauffer Technical – William Haddon (EOL/CDS) and Wei-Yu Chang (ASP) Casual appointment and Scientific discussion Tammy Weckwerth Jothiram Vivekanandan Wen-Chau Lee Hosting and paying the bills – NCAR/EOL/RSF

Custom Editing and Display of Reduced Information in Cartesian space Software system for the merger, analysis and display of three-dimensional gridded datasets Primarily for analysis of radar measurements Unfolding of Doppler radar radial velocities Synthesis of particle motion (u, v, W=w-Wt) Computation of Wt = a*(Z^b) * (density correction) Integration of the mass continuity equation for vertical air motion (w) Analysis of non-radar measurements Specialized systems with output in CEDRIC format Structured as fields

CEDRIC and CCOPE 1981 Cooperative COnvective Precipitation Experiment Doppler radars: NCAR CP-2, 3, & 4; NOAA C, D, & E Aircraft: 13 Mesonet: 80 CEDRIC – merge radar, aircraft, & mesonet SPRINT – radar ACANAL – aircraft SMANAL - mesonet

Relevant Publications Mohr, C. G. , L. J. Miller, R. L. Vaughn and H. W. Frank, 1986: The merger of mesoscale datasets into a common Cartesian format for efficient and systematic analysis, J. Atmos. Oceanic Technol. , 3, 143 -161. Miller, L. Jay, John D. Tuttle, and Charles A. Knight, 1988: Airflow and hail growth in a severe northern High Plains supercell, J. Atmos. Sci. , 4, 736 -762. Miller, L. Jay, John D. Tuttle, and G. Brant Foote, 1990: Precipitation production in a large Montana hailstorm: Airflow and particle growth trajectories, J. Atmos. Sci. , 13, 1619 -1646.

Overview of discussion topics Doppler radial velocity – projection of particle motion (u, v, W = w-w_t) along radar beam Geometry associated with multiple radars Inconsistencies or representativeness Two- and three-equation solutions for (u, v, W) Integration of mass continuity equation for w Solution includes variances (u, v, w-w_t) Synthesis quality measures (USTD, VSTD, WSTD)

Doppler Radar Wind Synthesis Interpolate radar data to common analysis grid using SPRINT or REORDER Unfold and edit radial velocities for all radars Transform non-orthogonal radial velocities to orthogonal particle motion Two- or three-equation solution Overdetermined two- or three-equation solution Integrate mass continuity for vertical air motion Upward, downward, or variational Iterative when two-equation (u, v) winds

Radar pulse-volume averaging: Radial velocity and the Cartesian components of particle motion

Sources of Errors in Particle Motion Errors in mean radial velocity estimates Inaccuracies in pulse-volume locations Radar location and/or antenna pointing errors Ranging errors and propagation effects Inconsistencies of pulse-volume averaging Mean radial velocity is reflectivity-weighted average Different pulse-volume shapes and sizes Geometry of transformations from radial velocities to Cartesian components Non-stationarity of fields during data collection Inadequate spatial and temporal sampling

Triple Radar Three equations with four unknowns Either fallspeed from reflectivity Or mass continuity

Linear Equations Three and two equation solutions

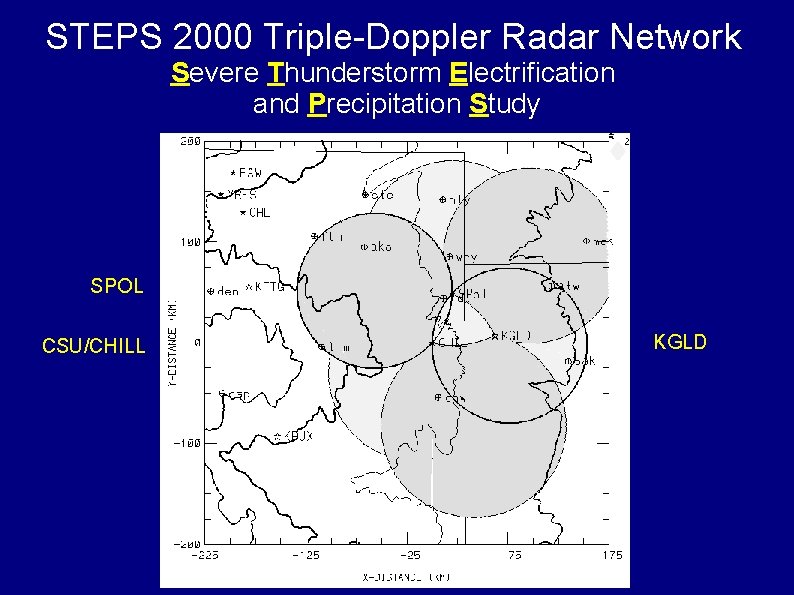
STEPS 2000 Triple-Doppler Radar Network Severe Thunderstorm Electrification and Precipitation Study SPOL CSU/CHILL KGLD

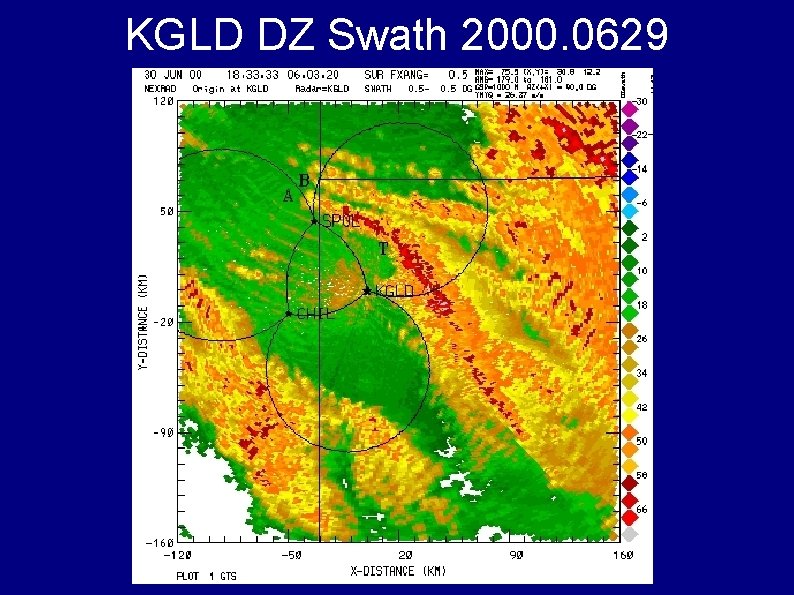
KGLD DZ Swath 2000. 0629

Three-equation (Triple Doppler) UV UV - Black SPOL - G CHILL - B KGLD - R

Two-equation (Dual Doppler) UV UV - Black SPOL - G CHILL - B KGLD - R

Three Equation Variances Standard deviations from normalized variances Ustd, Vstd, Wstd

Two Equation Variances Standard deviations from normalized variances Ustd, Vstd

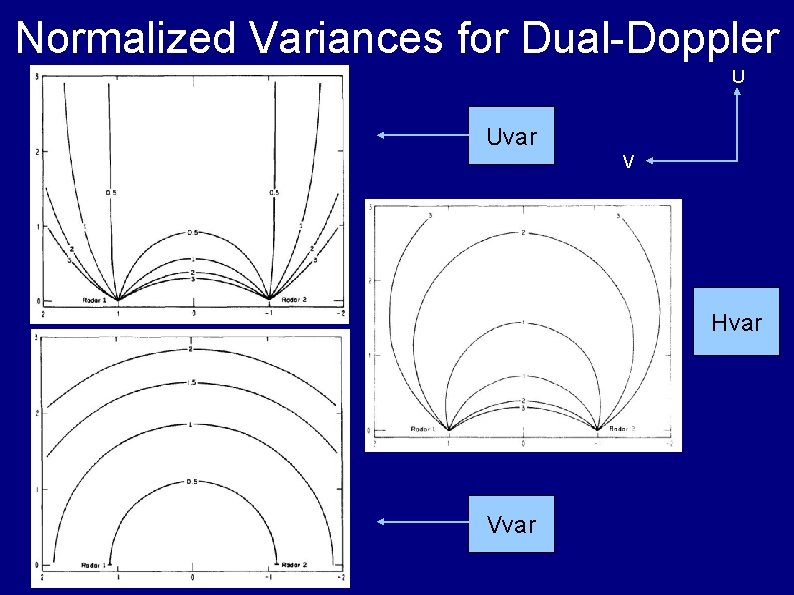
Normalized Variances for Dual-Doppler U Uvar V Hvar Vvar

Advection during synthesis Normal Equations: Three and two

SYNTHES Command

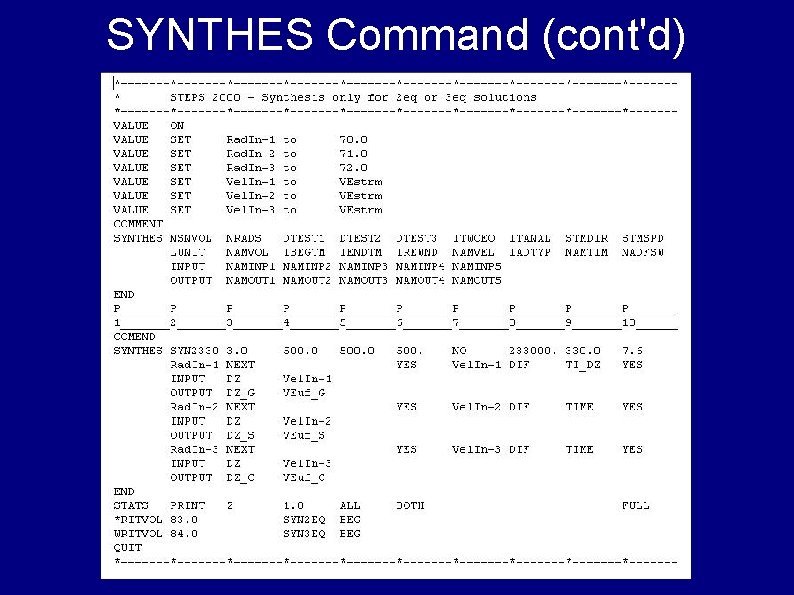
SYNTHES Command (cont'd)

U, V, W std & EWU EWV

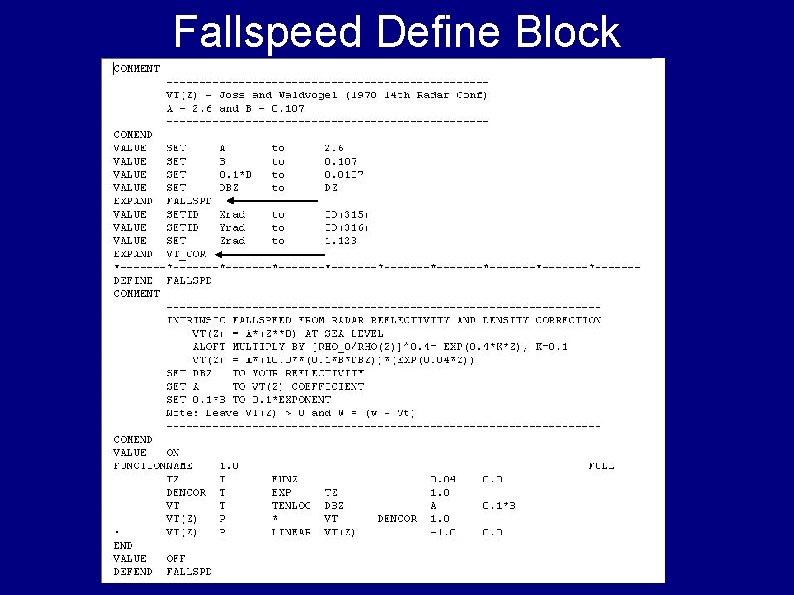
Fallspeed Define Block

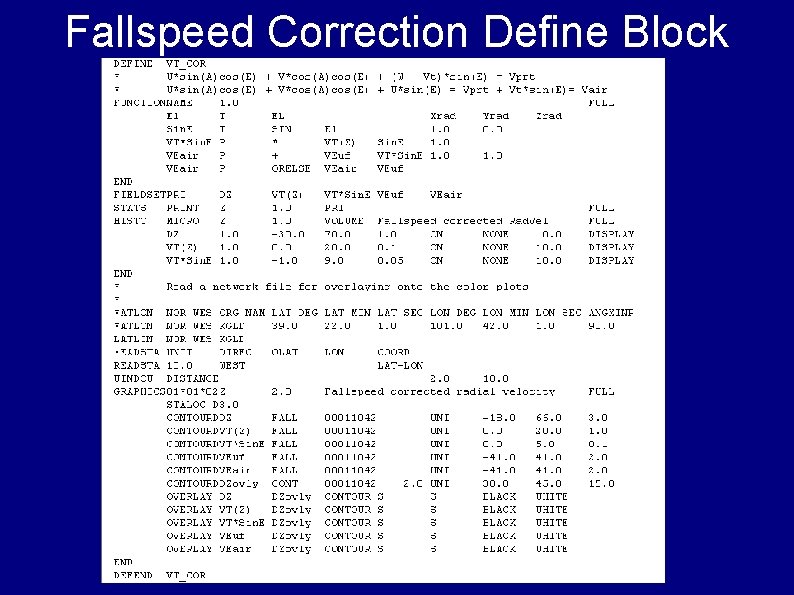
Fallspeed Correction Define Block

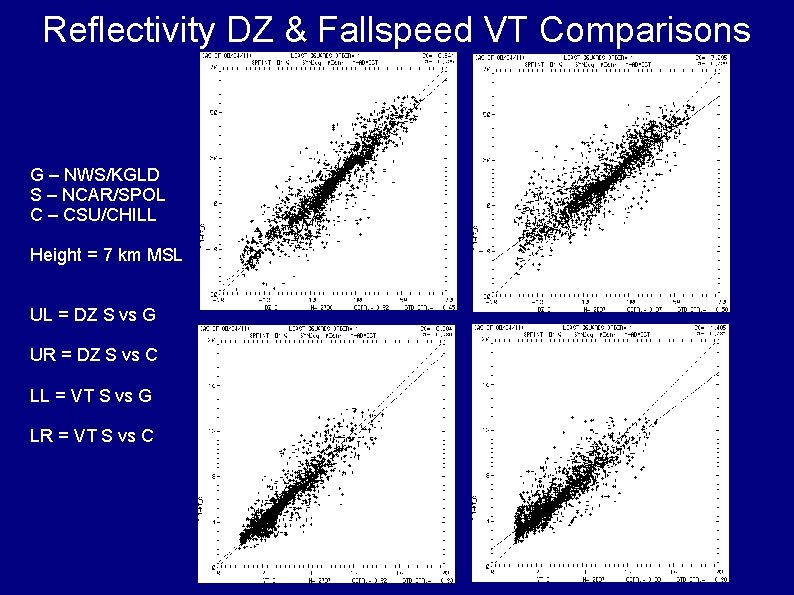
Reflectivity DZ & Fallspeed VT Comparisons G – NWS/KGLD S – NCAR/SPOL C – CSU/CHILL Height = 7 km MSL UL = DZ S vs G UR = DZ S vs C LL = VT S vs G LR = VT S vs C

Iterative Integration of Mass Continuity A A= Left hand side B= First term RHS C = Second term RHS

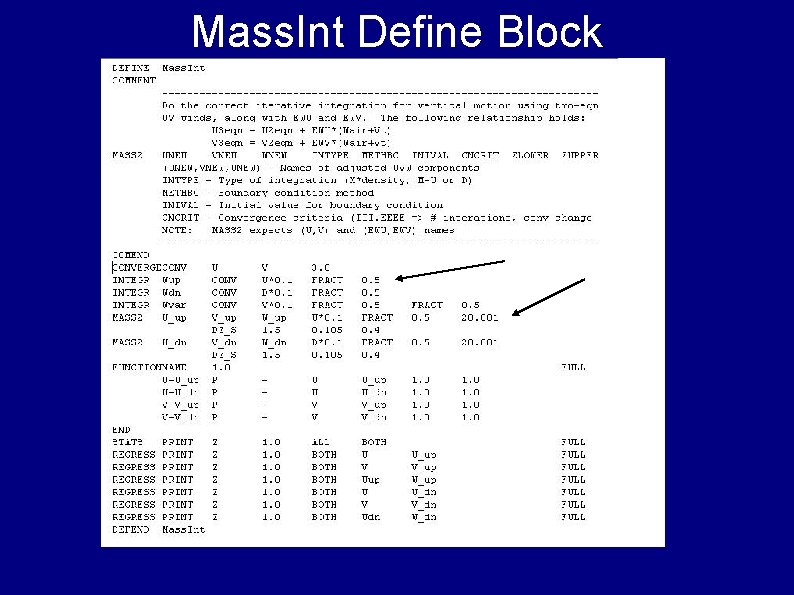
Mass. Int Define Block

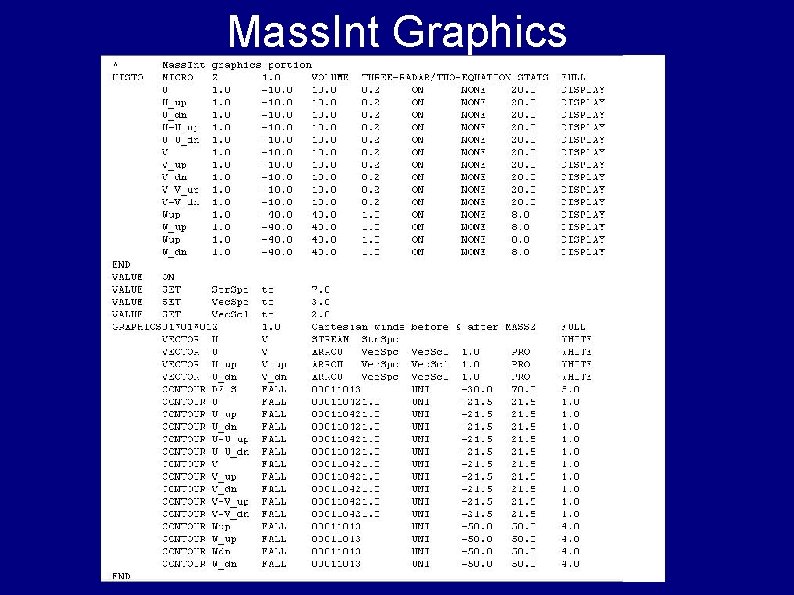
Mass. Int Graphics

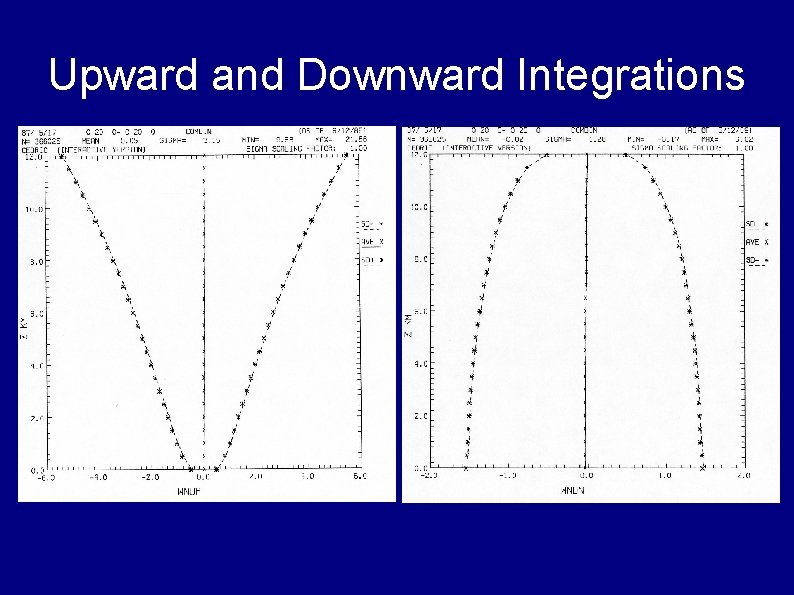
Integration of Mass Continuity Equation

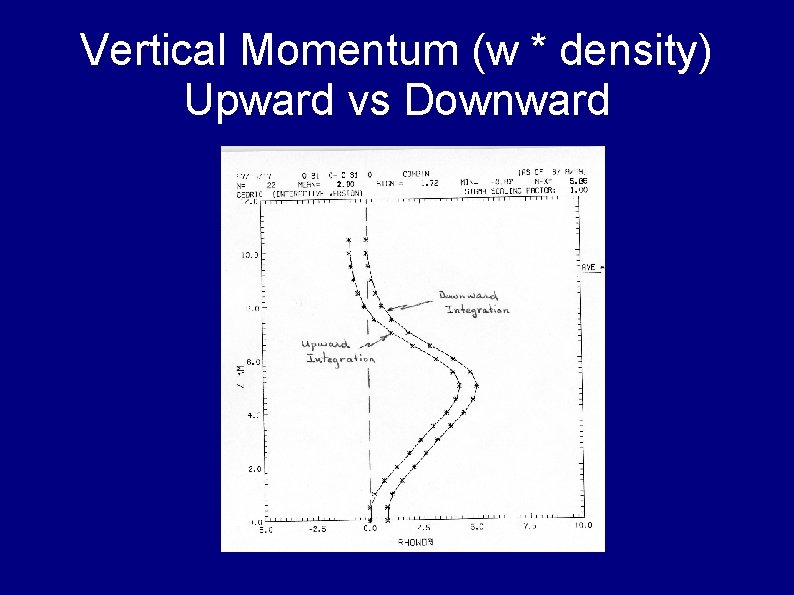
Upward and Downward Integrations

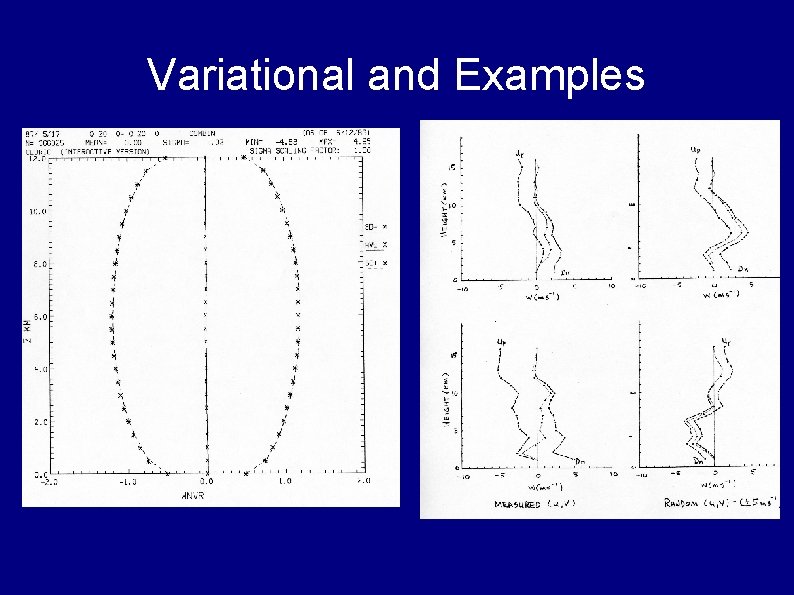
Variational and Examples

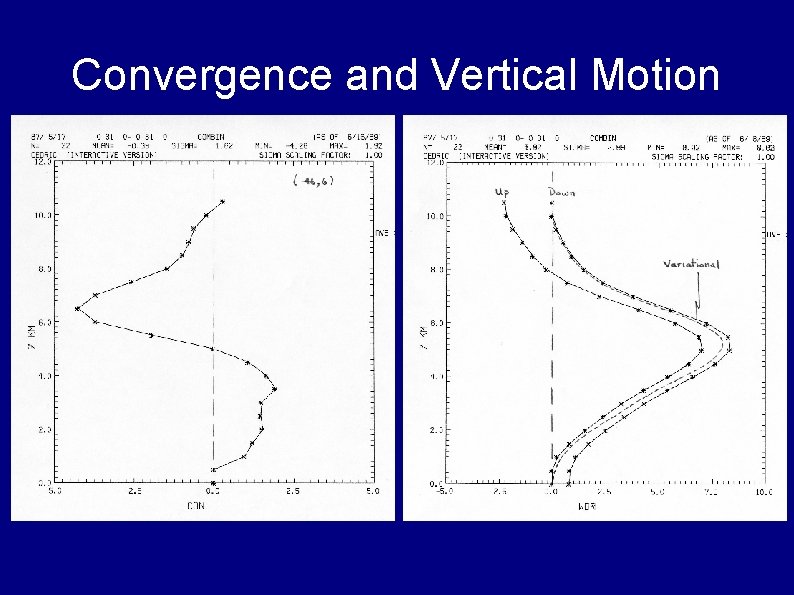
Sources of Errors in Vertical Motion when Using Mass Continuity Equation Inaccuracies in horizontal convergence estimates Errors in horizontal wind components Inadequacies of finite difference estimator Incorrect estimates of particle fallspeed Errors in boundary conditions (upper and lower) Deficiencies in numerical integration methods Misrepresentation of air density

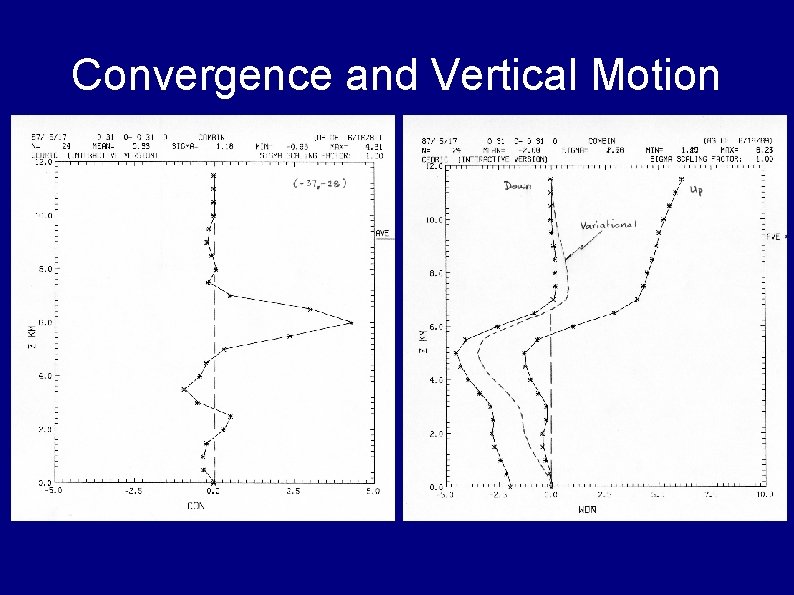
Convergence and Vertical Motion

Vertical Momentum (w * density) Upward vs Downward

Convergence and Vertical Motion

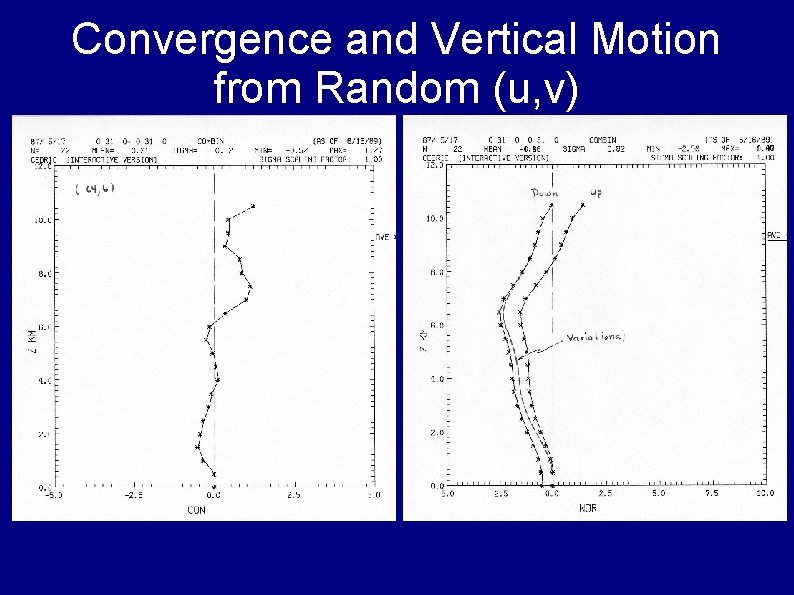
Convergence and Vertical Motion from Random (u, v)

Vertical Air Motion from Integrations

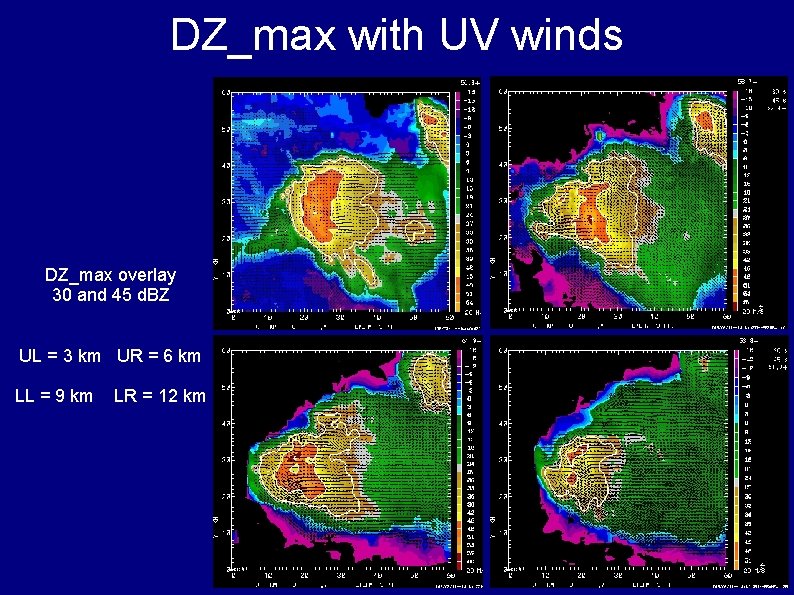
DZ_max with UV winds DZ_max overlay 30 and 45 d. BZ UL = 3 km UR = 6 km LL = 9 km LR = 12 km

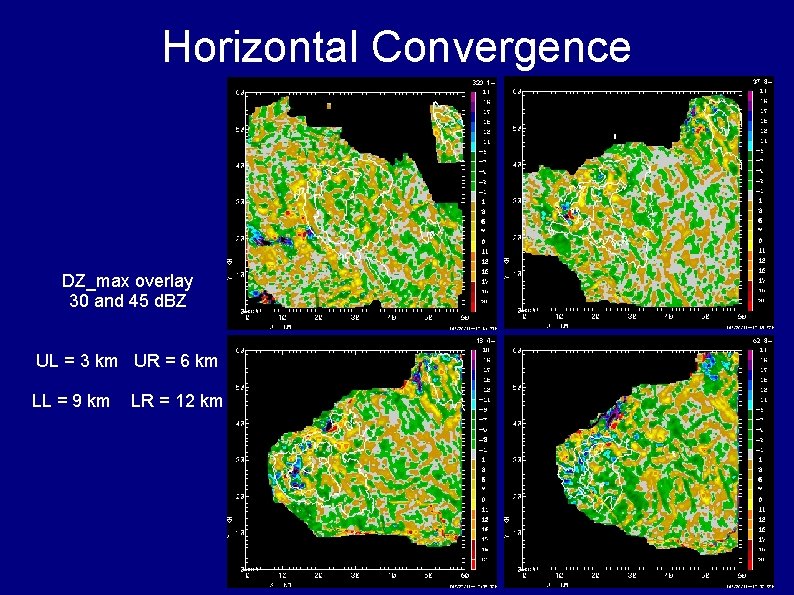
Horizontal Convergence DZ_max overlay 30 and 45 d. BZ UL = 3 km UR = 6 km LL = 9 km LR = 12 km

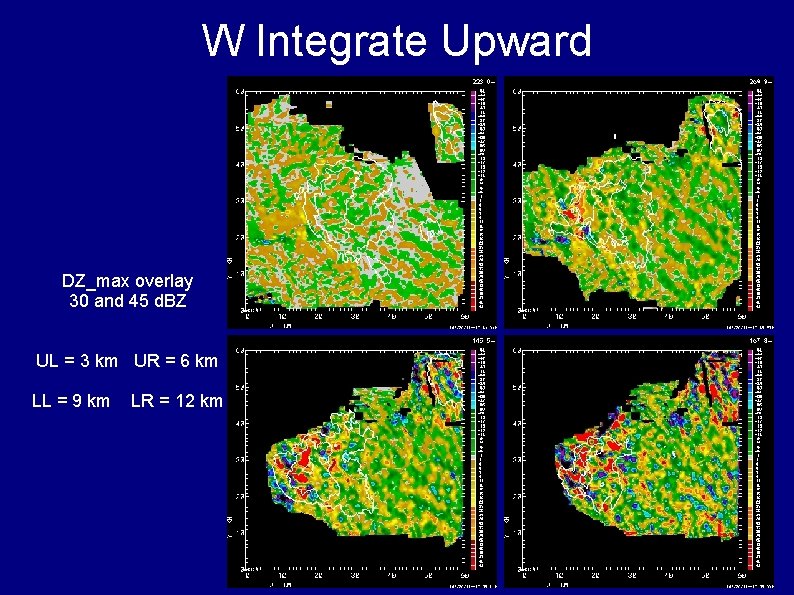
W Integrate Upward DZ_max overlay 30 and 45 d. BZ UL = 3 km UR = 6 km LL = 9 km LR = 12 km

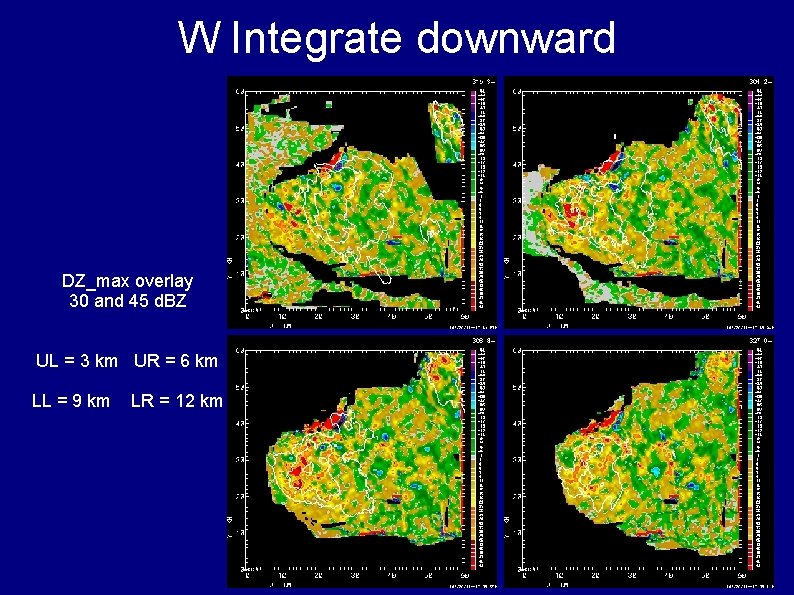
W Integrate downward DZ_max overlay 30 and 45 d. BZ UL = 3 km UR = 6 km LL = 9 km LR = 12 km

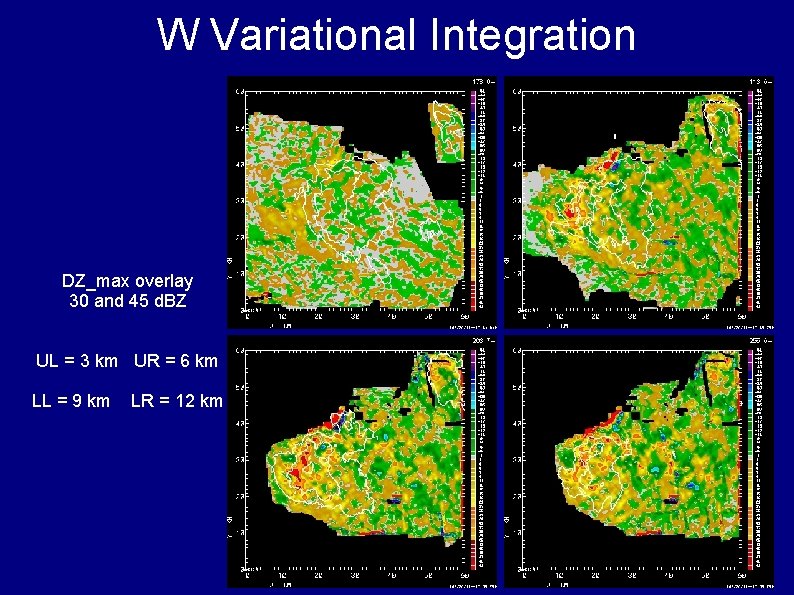
W Variational Integration DZ_max overlay 30 and 45 d. BZ UL = 3 km UR = 6 km LL = 9 km LR = 12 km

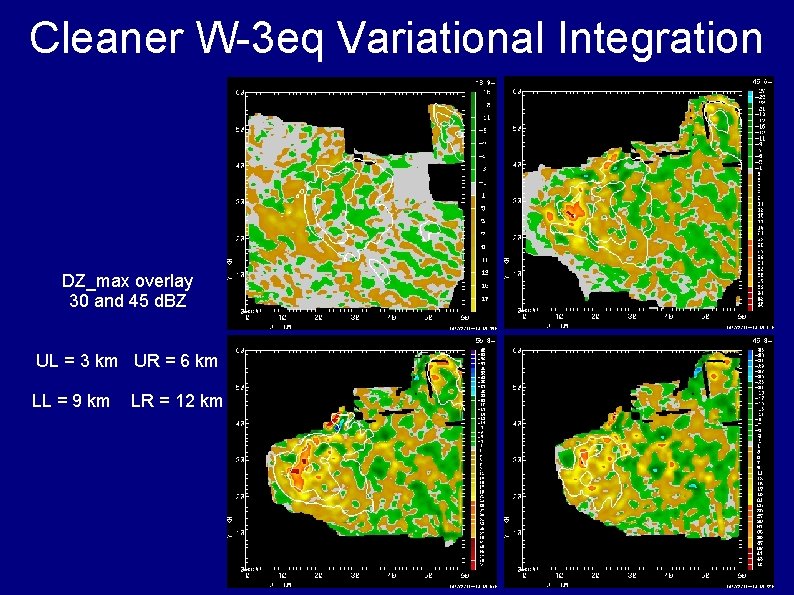
Cleaner W-3 eq Variational Integration DZ_max overlay 30 and 45 d. BZ UL = 3 km UR = 6 km LL = 9 km LR = 12 km

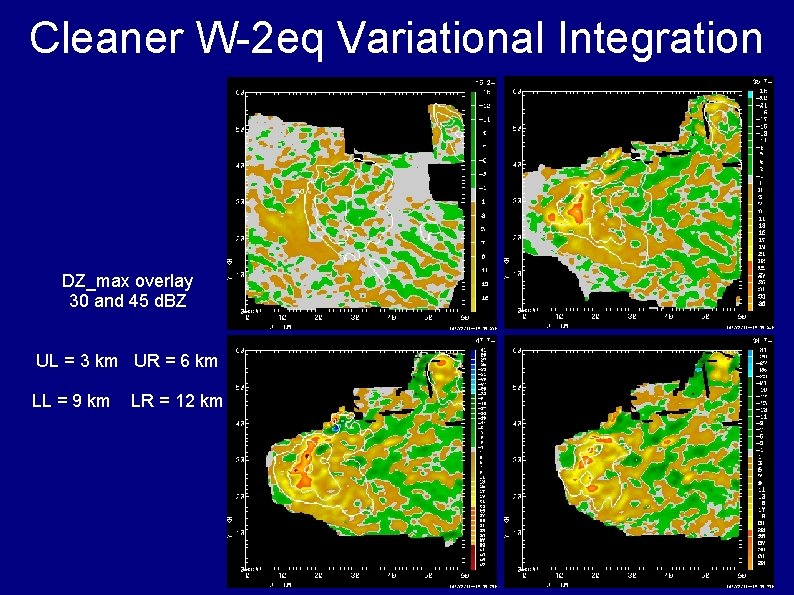
Cleaner W-2 eq Variational Integration DZ_max overlay 30 and 45 d. BZ UL = 3 km UR = 6 km LL = 9 km LR = 12 km

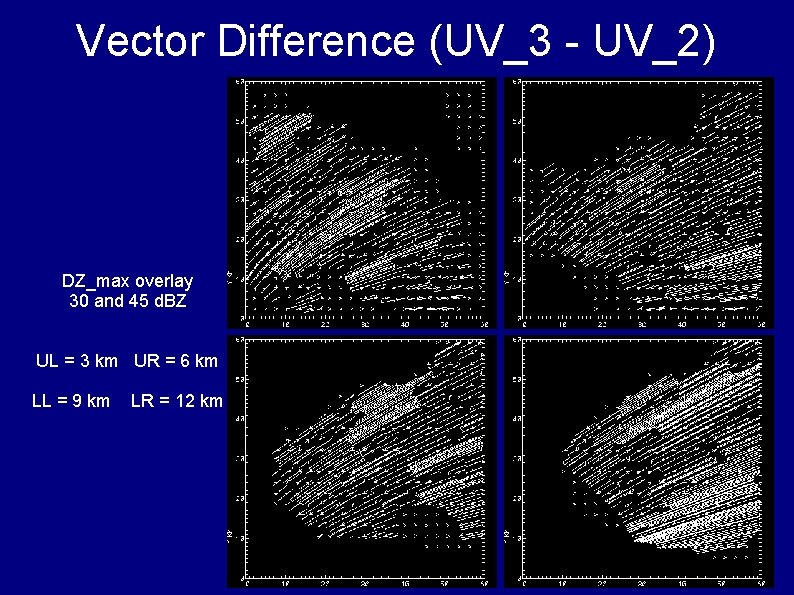
Vector Difference (UV_3 - UV_2) DZ_max overlay 30 and 45 d. BZ UL = 3 km UR = 6 km LL = 9 km LR = 12 km

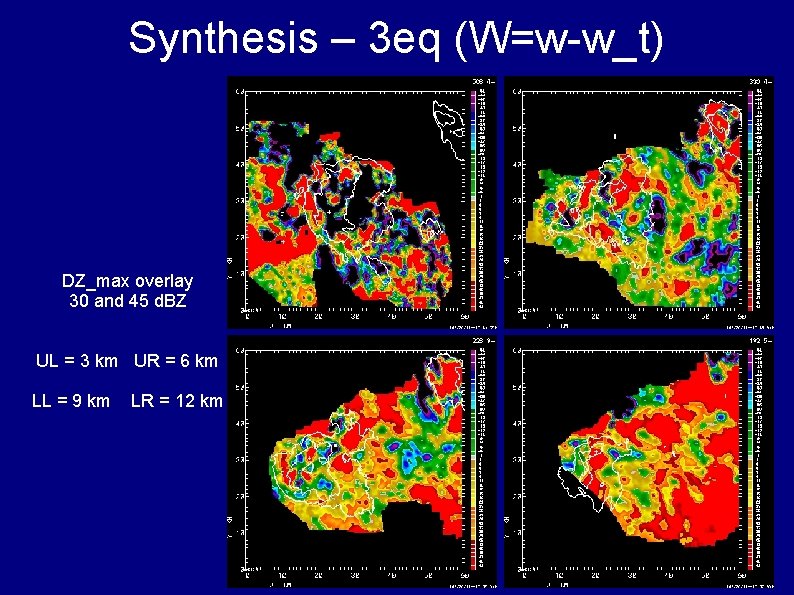
Synthesis – 3 eq (W=w-w_t) DZ_max overlay 30 and 45 d. BZ UL = 3 km UR = 6 km LL = 9 km LR = 12 km

“Why you should be critical of results” Radial velocities may not be representative Radars observe dissimilar spatial volumes Mean velocities are reflectivity-weighted spatial averages Vertical component of particle motion typically poorly observed Cannot be ignored since it is bias error Integration of mass continuity and separating vertical air motion from fallspeed Boundary conditions can only be “best guesses” Intrinsic fallspeeds must be estimated