Some Efficient Sorting Algorithms Two of the most

Some Efficient Sorting Algorithms • Two of the most popular sorting algorithms are based on divide-and-conquer approach. – Quick sort – Merge sort • Basic concept: sort (list) { if the list has length greater than 1 { Partition the list into lowlist and highlist; sort (lowlist); sort (highlist); combine (lowlist, highlist); } } 9/9/2021 Programming and Data Structure 1

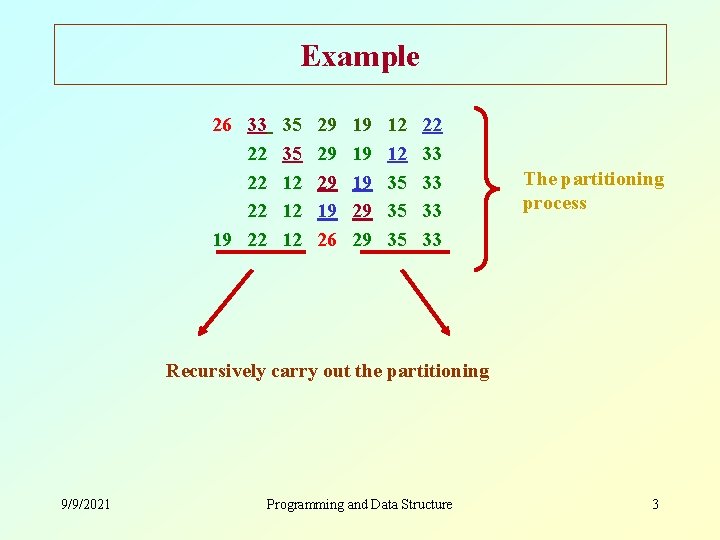
Quicksort • At every step, we select a pivot element in the list (usually the first element). – We put the pivot element in the final position of the sorted list. – All the elements less than or equal to the pivot element are to the left. – All the elements greater than the pivot element are to the right. 9/9/2021 Programming and Data Structure 2

Example 26 33 22 22 22 19 22 35 35 12 12 12 29 29 29 19 26 19 19 19 29 29 12 12 35 35 35 22 33 33 The partitioning process Recursively carry out the partitioning 9/9/2021 Programming and Data Structure 3

Tree: A Non-linear Data Structure 9/9/2021 Programming and Data Structure 4

Background • Linked lists use dynamic memory allocation, and hence enjoys some advantages over static representations using arrays. • A problem – Searching an ordinary linked list for a given element. • Time complexity O(n). – Can the nodes in a linked list be rearranged so that we can search in O(nlog 2 n) time? 9/9/2021 Programming and Data Structure 5

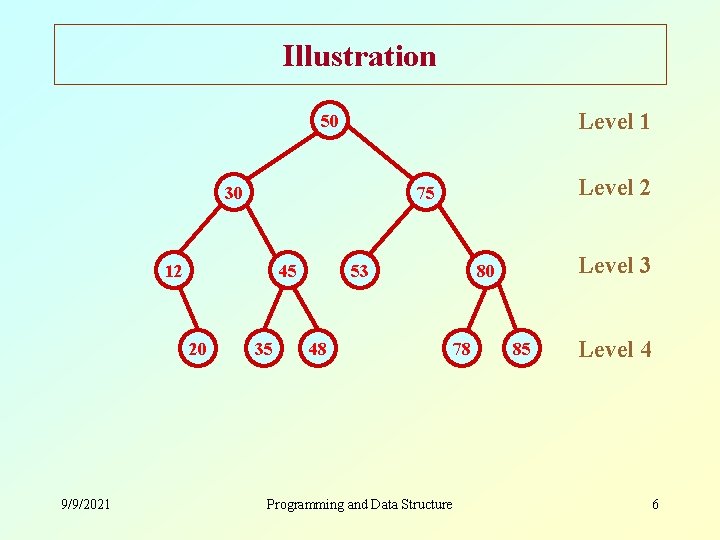
Illustration Level 1 50 30 12 45 20 9/9/2021 Level 2 75 35 53 48 Programming and Data Structure Level 3 80 78 85 Level 4 6

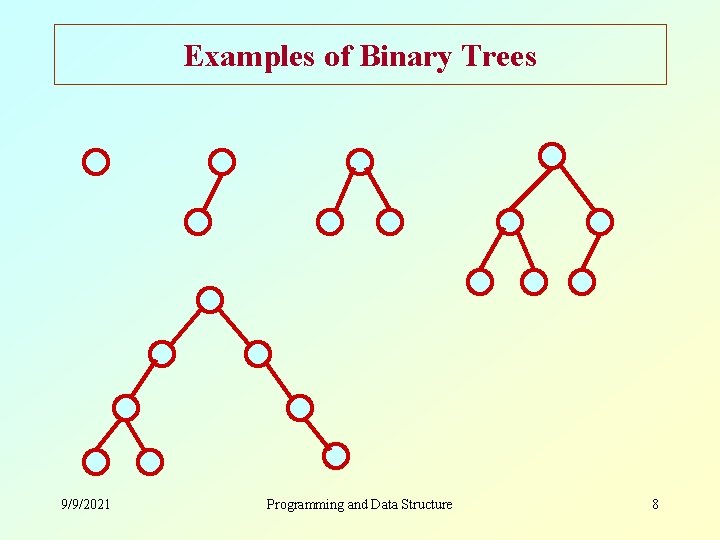
Binary Tree • A new data structure – Binary means two. • Definition – A binary tree is either empty, or it consists of a node called the root, together with two binary trees called the left subtree and the right subtree. Root Left subtree 9/9/2021 Right subtree Programming and Data Structure 7

Examples of Binary Trees 9/9/2021 Programming and Data Structure 8

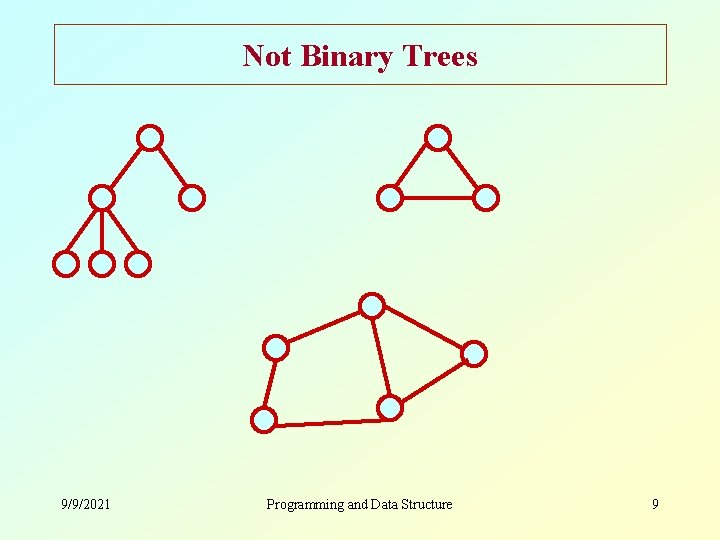
Not Binary Trees 9/9/2021 Programming and Data Structure 9

Binary Search Trees • A particular form of binary tree suitable for searching. • Definition – A binary search tree is a binary tree that is either empty or in which each node contains a key that satisfies the following conditions: • All keys (if any) in the left subtree of the root precede the key in the root. • The key in the root precedes all keys (if any) in its right subtree. • The left and right subtrees of the root are again binary search trees. 9/9/2021 Programming and Data Structure 10

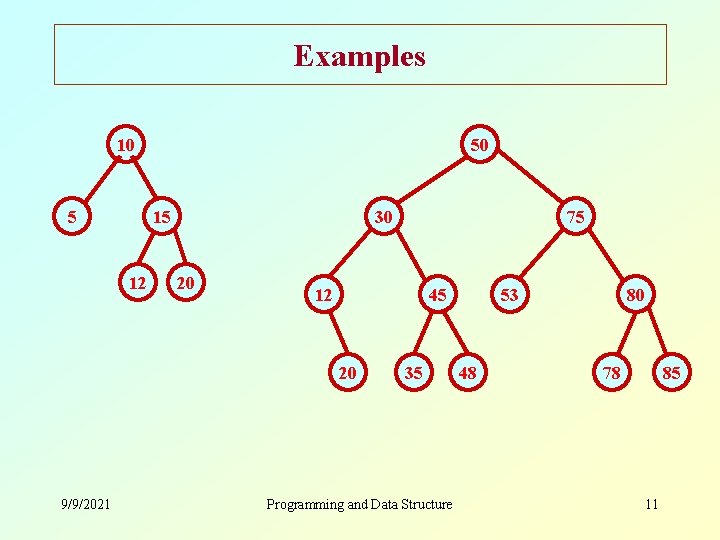
Examples 10 5 50 15 12 30 20 12 45 20 9/9/2021 75 35 Programming and Data Structure 53 48 80 78 85 11

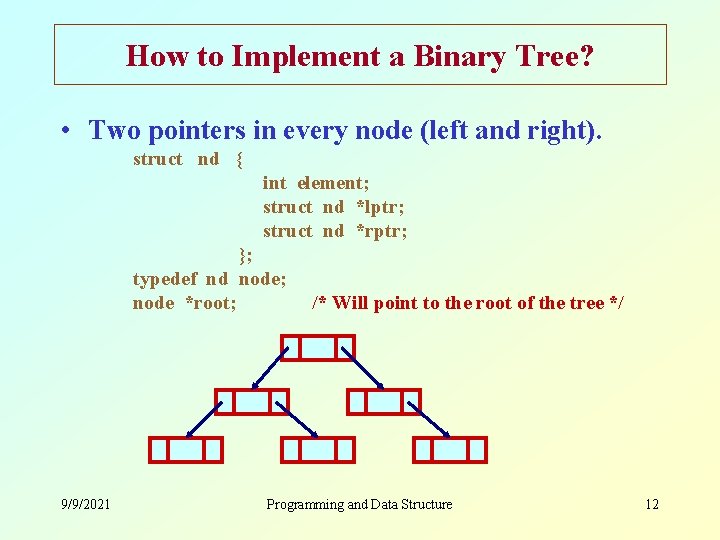
How to Implement a Binary Tree? • Two pointers in every node (left and right). struct nd { int element; struct nd *lptr; struct nd *rptr; }; typedef nd node; node *root; 9/9/2021 /* Will point to the root of the tree */ Programming and Data Structure 12

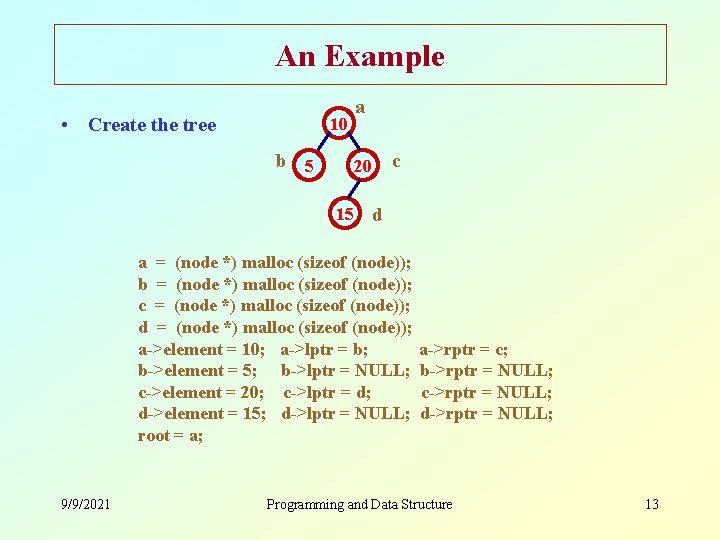
An Example • Create the tree 10 a b 5 c 20 15 d a = (node *) malloc (sizeof (node)); b = (node *) malloc (sizeof (node)); c = (node *) malloc (sizeof (node)); d = (node *) malloc (sizeof (node)); a->element = 10; a->lptr = b; b->element = 5; b->lptr = NULL; c->element = 20; c->lptr = d; d->element = 15; d->lptr = NULL; root = a; 9/9/2021 a->rptr = c; b->rptr = NULL; c->rptr = NULL; d->rptr = NULL; Programming and Data Structure 13

Traversal of Binary Trees • In many applications, it is required to move through all the nodes of a binary tree, visiting each node in turn. – For n nodes, there exists n! different orders. – Three traversal orders are most common: • Inorder traversal • Preorder traversal • Postorder traversal 9/9/2021 Programming and Data Structure 14

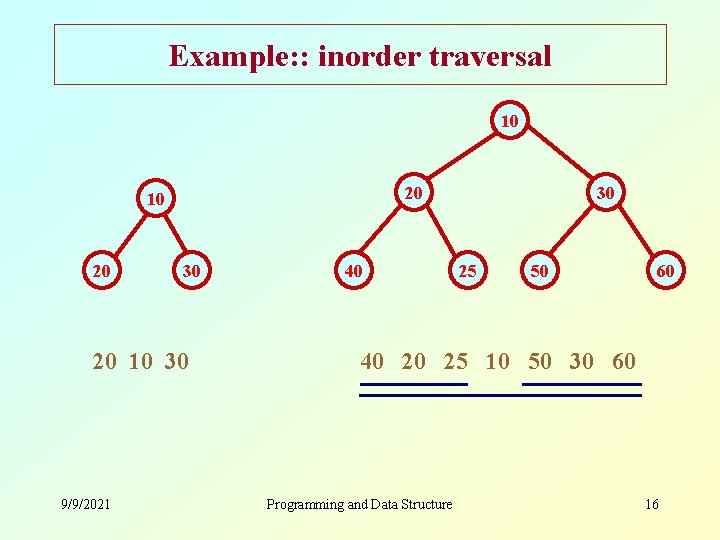
Inorder Traversal • Recursively, perform the following three steps: – Visit the left subtree. – Visit the root. – Visit the right subtree. LEFT-ROOT-RIGHT 9/9/2021 Programming and Data Structure 15

Example: : inorder traversal 10 20 30 20 10 30 9/9/2021 40 30 25 50 60 40 20 25 10 50 30 60 Programming and Data Structure 16

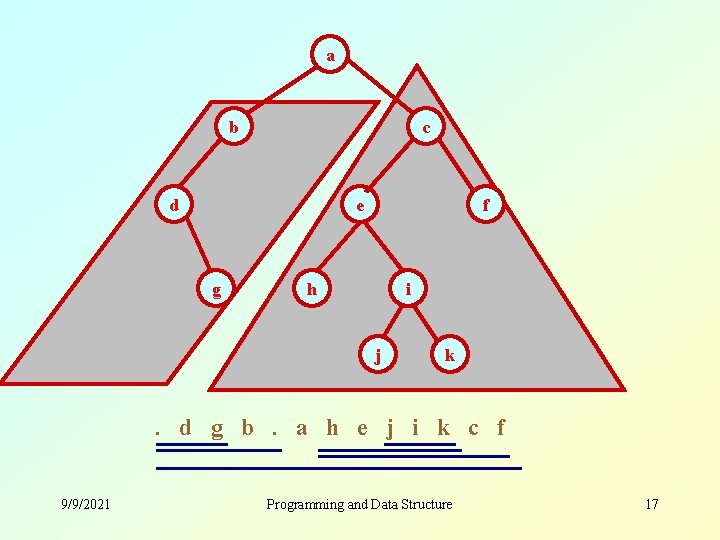
a b c d e g f h i j k . d g b. a h e j i k c f 9/9/2021 Programming and Data Structure 17

Preorder Traversal • Recursively, perform the following three steps: – Visit the root. – Visit the left subtree. – Visit the right subtree. ROOT-LEFT-RIGHT 9/9/2021 Programming and Data Structure 18

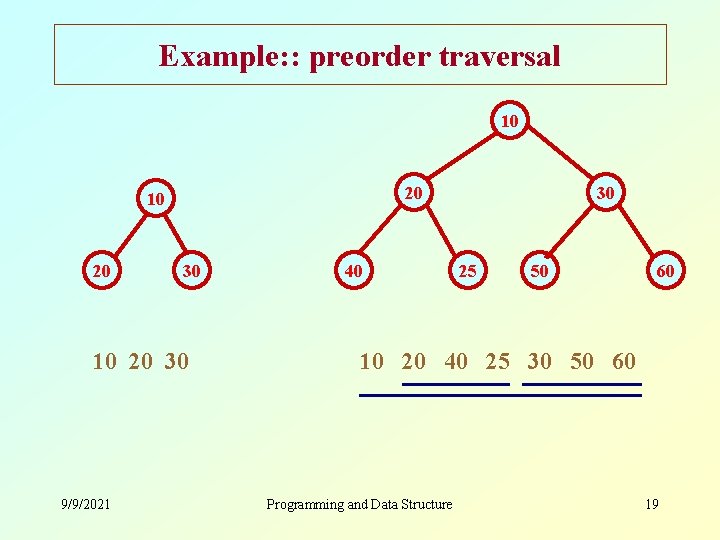
Example: : preorder traversal 10 20 30 9/9/2021 40 30 25 50 60 10 20 40 25 30 50 60 Programming and Data Structure 19

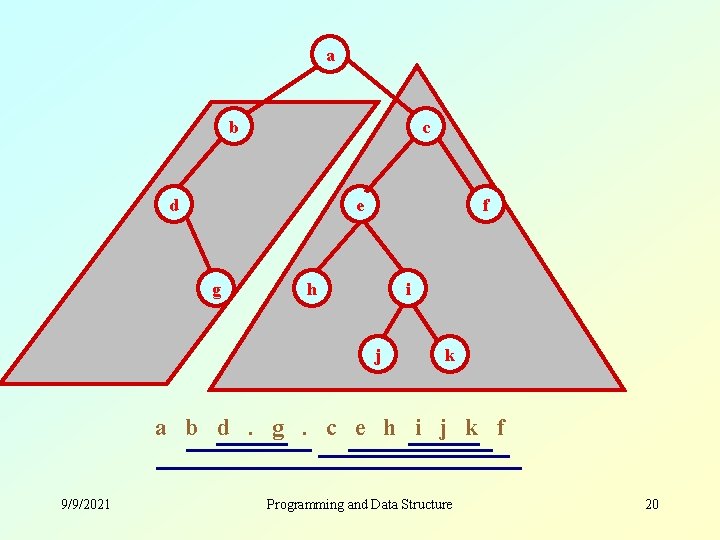
a b c d e g f h i j k a b d. g. c e h i j k f 9/9/2021 Programming and Data Structure 20

Postorder Traversal • Recursively, perform the following three steps: – Visit the left subtree. – Visit the right subtree. – Visit the root. LEFT-RIGHT-ROOT 9/9/2021 Programming and Data Structure 21

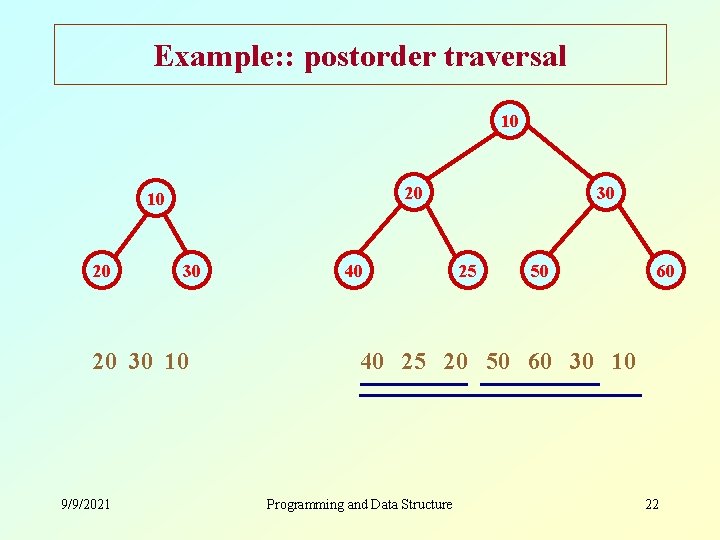
Example: : postorder traversal 10 20 30 10 9/9/2021 40 30 25 50 60 40 25 20 50 60 30 10 Programming and Data Structure 22

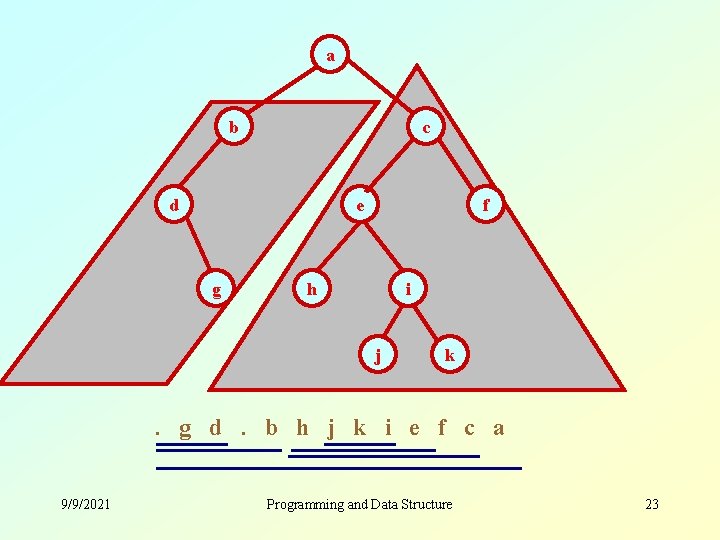
a b c d e g f h i j k . g d. b h j k i e f c a 9/9/2021 Programming and Data Structure 23

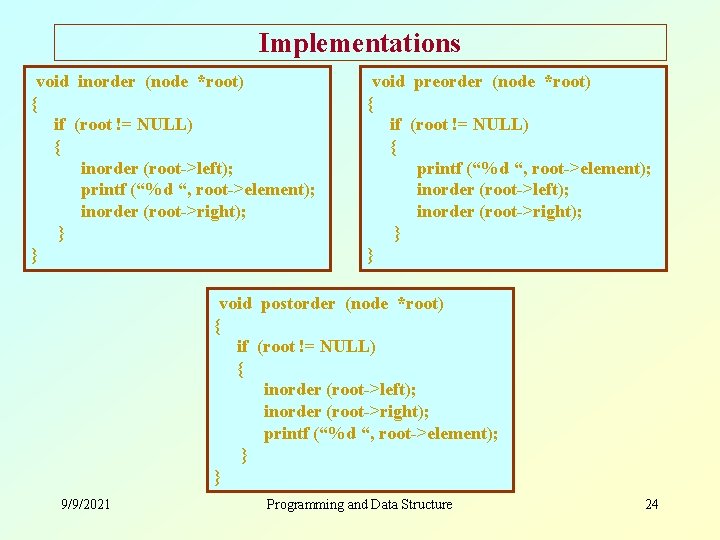
Implementations void inorder (node *root) { if (root != NULL) { inorder (root->left); printf (“%d “, root->element); inorder (root->right); } } void preorder (node *root) { if (root != NULL) { printf (“%d “, root->element); inorder (root->left); inorder (root->right); } } void postorder (node *root) { if (root != NULL) { inorder (root->left); inorder (root->right); printf (“%d “, root->element); } } 9/9/2021 Programming and Data Structure 24

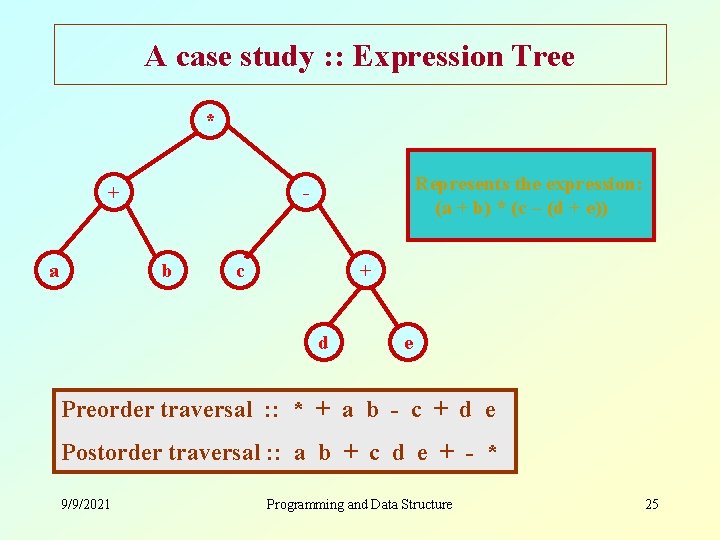
A case study : : Expression Tree * + a Represents the expression: (a + b) * (c – (d + e)) - b c + d e Preorder traversal : : * + a b - c + d e Postorder traversal : : a b + c d e + - * 9/9/2021 Programming and Data Structure 25

Binary Search Tree (Revisited) • Given a binary search tree, how to write a program to search for a given element? • Easy to write a recursive program. int search (node *root, int key) { if (root != NULL) { if (root->element == key) return (1); else if (root->element > key) search (root->lptr, key); else search (root->rptr, key); } } 9/9/2021 Programming and Data Structure 26

Some Points to Note • The following operations are a little complex and are not discussed here. – Inserting a node into a binary search tree. – Deleting a node from a binary search tree. 9/9/2021 Programming and Data Structure 27

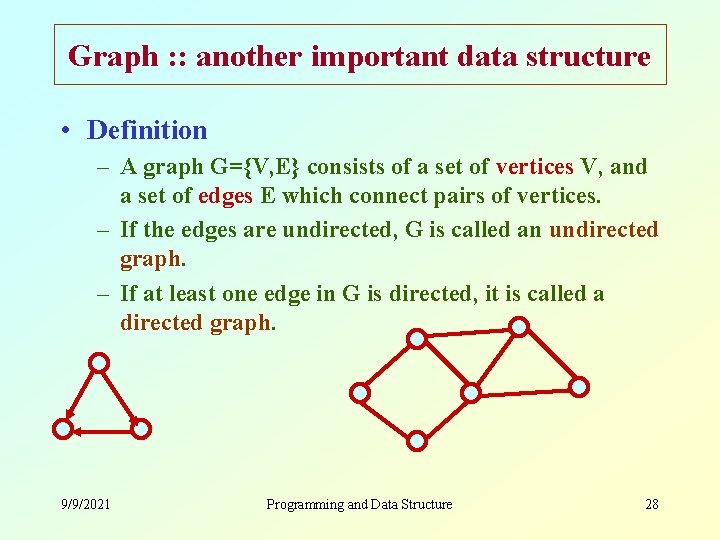
Graph : : another important data structure • Definition – A graph G={V, E} consists of a set of vertices V, and a set of edges E which connect pairs of vertices. – If the edges are undirected, G is called an undirected graph. – If at least one edge in G is directed, it is called a directed graph. 9/9/2021 Programming and Data Structure 28

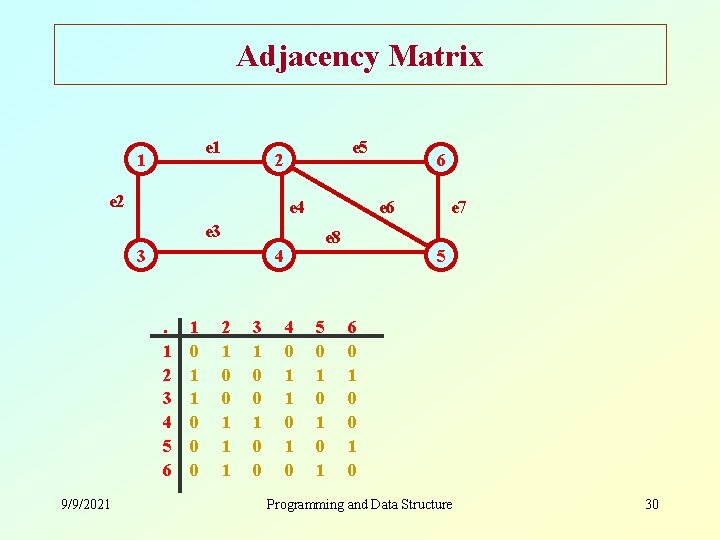
How to represent a graph in a program? • Many ways – Adjacency matrix – Incidence matrix, etc. 9/9/2021 Programming and Data Structure 29

Adjacency Matrix e 1 1 e 5 2 e 4 e 3 3 . 1 2 3 4 5 6 9/9/2021 1 0 0 0 2 1 0 0 1 1 1 3 1 0 0 e 6 e 8 4 4 0 1 1 0 6 5 0 1 0 1 e 7 5 6 0 1 0 Programming and Data Structure 30

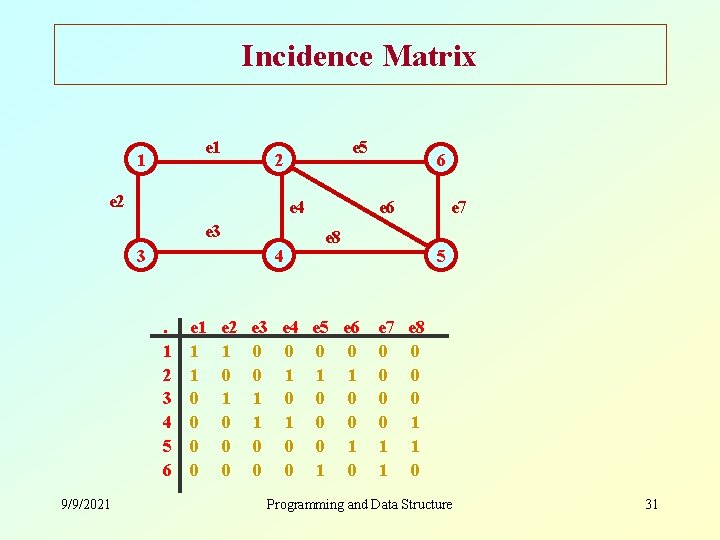
Incidence Matrix e 1 1 e 5 2 e 4 e 3 3 4 . 1 2 3 4 5 6 9/9/2021 e 1 1 1 0 0 e 2 1 0 0 0 e 3 0 0 1 1 0 0 e 4 0 1 0 0 6 e 7 e 8 e 5 e 6 0 0 1 1 0 5 e 7 0 0 1 1 e 8 0 0 0 1 1 0 Programming and Data Structure 31

9/9/2021 Programming and Data Structure 32