Some Classification Algorithms in Machine Learning Presented by

Some Classification Algorithms in Machine Learning Presented by Asst. Prof. Mahajan Uchita Vidyadhar Department of Statistics, KCE’s Society PGCSTR, Jalgaon. 1

Content Ø Ø Ø Ø Ø Introduction Machine learning methodologies What is classification? What is machine learning? Types of classification algorithm in machine learning Decision tree Naïve bayes Applications Reference Acknowledgement 2
Introduction 3

What is Classification? § Classification is the process of predicting the class of given data points. Classes are sometimes called as target / labels or categories. § Classification belongs to the category of supervised learning where the target also provided with the input data. § Here, we are going to deal with two important classification algorithms § Decision Tree § Naïve Bayes What is Machine learning? § Machine learning explores the study and construction of algorithms that can learn from and make prediction on data. § Closely related to computational Statistics. 4

Machine Learning Methodologies § Supervised learning Learning from labelled data. § Classification, regression, forecasting, prediction. § § Unsupervised learning Learning from unlabeled data. § Clustering, dimension reduction. § Reinforcement learning § model learns from a series of actions by maximizing a reward function. § Example: -training of self-driving car using feedback from the 5 environment. §
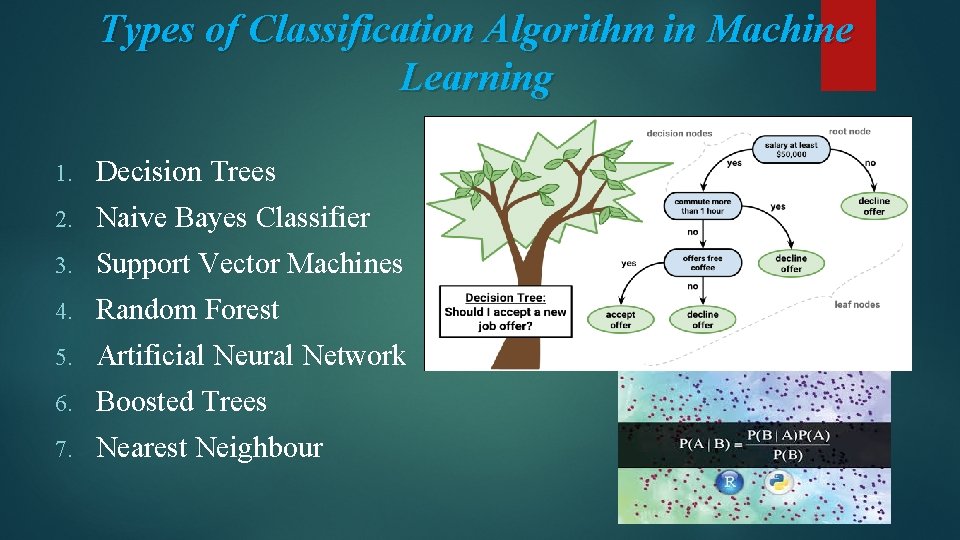
Types of Classification Algorithm in Machine Learning 1. Decision Trees 2. Naive Bayes Classifier 3. Support Vector Machines 4. Random Forest 5. Artificial Neural Network 6. Boosted Trees 7. Nearest Neighbour 6

Decision Tree 7 § It is a type of supervised algorithm. § We split the population into two or more homogeneous sets. § Decision trees classify instances or examples by starting at the root of the tree and moving through it until a leaf node. § Decision tree is a classifier in the form of a tree structure § § Decision node: -Specifies a test on a single attribute. § Leaf node: -Indicates the value of the target attribute. § Branch: -Split of one attribute. § Path: -A disjunction of test to make the final decision. Decision tree can handle both categorical and numerical data.
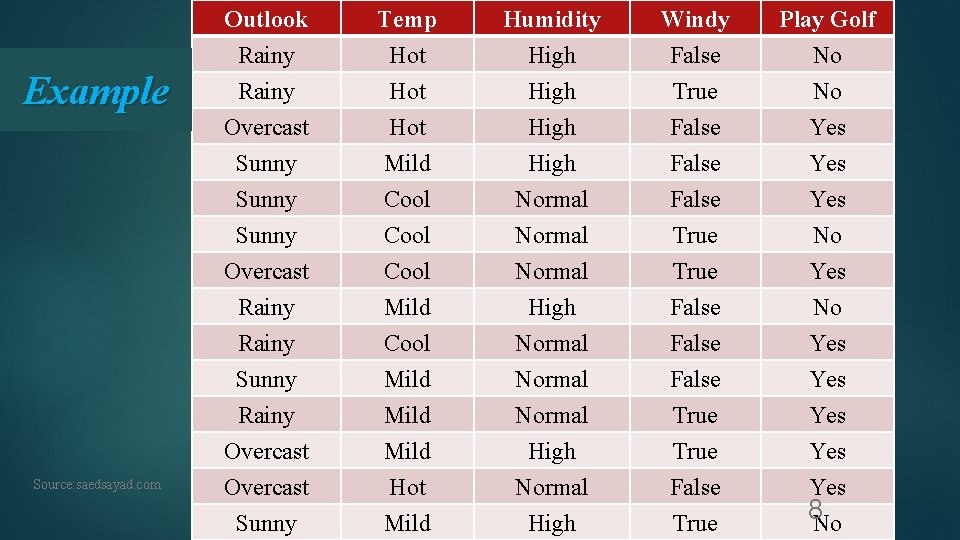
Example Source: saedsayad. com Outlook Rainy Overcast Temp Hot Hot Humidity High Windy False True False Play Golf No No Yes Sunny Mild Cool High Normal False True Yes No Overcast Rainy Sunny Rainy Overcast Cool Mild Hot Normal High Normal True False True False Yes No Yes Yes Yes Sunny Mild High True 8 No

Entropy 9 § A decision tree is built top-down from a root node and involves partitioning the data into subsets that contain instances with similar values (homogeneous). § ID 3 algorithm uses entropy to calculate the homogeneity of a sample. § If the sample is completely homogeneous the entropy is zero and if the sample is an equally divided it has entropy of one.

To build a decision tree, we need to calculate two types of entropy using frequency tables as follows Play Golf Yes No 9 5 10

b) Entropy using the frequency table of two attributes 11 Play Golf Yes No Sunny 3 2 0 Outlook Overcast 4 Rainy 2 Entropy(Play. Golf, Outlook) =P(Sunny)*E(3, 2)+P(Overcast)*E(4, 0)+P(Rainy)*E(2, 3) =(5/14)*0. 971+(4/14)*0. 0+(5/14)*0. 971 =0. 693 3 5 4 5 14

Information Gain 12

Step 2 13 § The dataset is then split on the different attributes. § The entropy for each branch is calculated. § Then it is added proportionally, to get total entropy for the split. § The resulting entropy is subtracted from the entropy before the split. § The result is the Information Gain, or decrease in entropy. § Gain(T, X)=E(T)-E(T, X) Gain(Play. Golf, Outlook)=E(Play. Golf)-E(play. Golf , Outlook) =0. 940 -0. 693 =0. 247
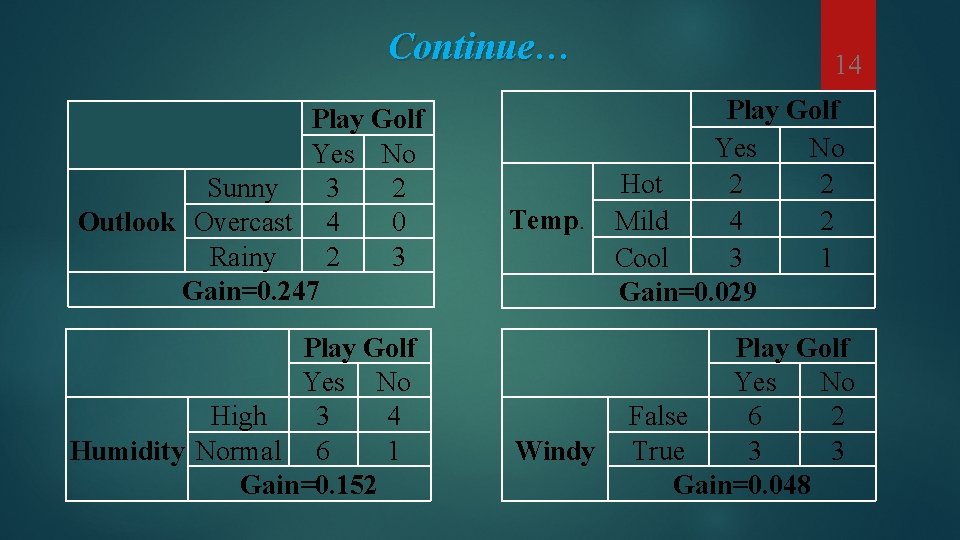
Continue… 14 Play Golf Yes No Sunny 3 2 Outlook Overcast 4 0 Rainy 2 3 Gain=0. 247 Play Golf Yes No Hot 2 2 Temp. Mild 4 2 Cool 3 1 Gain=0. 029 Play Golf Yes No High 3 4 Humidity Normal 6 1 Gain=0. 152 Play Golf Yes No False 6 2 Windy True 3 3 Gain=0. 048

Step 3 § Choose attribute with the largest information gain as the decision node. Play Golf Yes No Sunny 3 2 Outlook Overcast 4 0 Rainy 2 3 Gain=0. 247 15
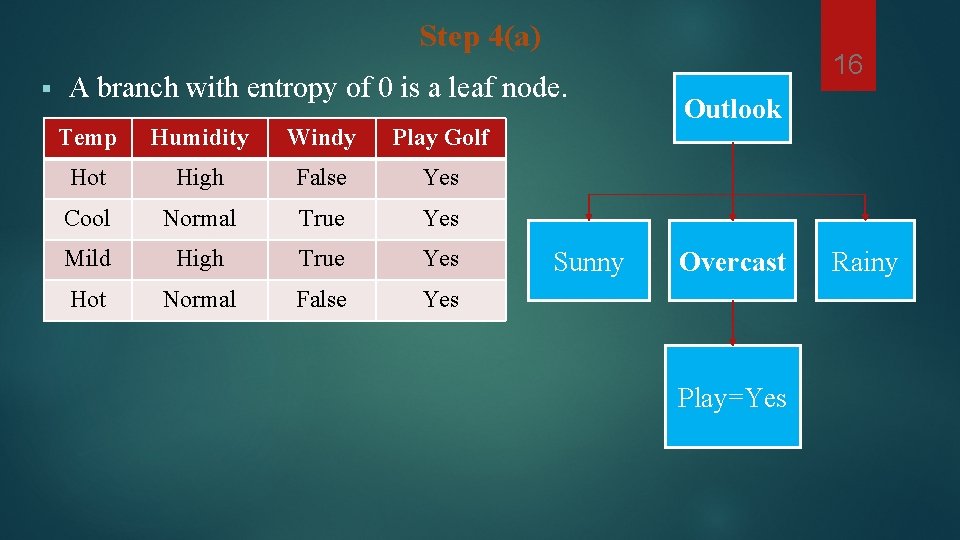
Step 4(a) § A branch with entropy of 0 is a leaf node. Temp Humidity Windy Play Golf Hot High False Yes Cool Normal True Yes Mild High True Yes Hot Normal False Yes Sunny 16 Outlook Overcast Play=Yes Rainy

Step 4(b) § A branch with entropy more than 0 needs further splitting. Temp Humidity Windy Play Golf Mild High False Yes Cool Normal False Yes Mild Normal False Yes Cool Normal True No Mild High True No 17 Outlook Sunny Overcast Windy Play=Yes False Play=Yes True Play=No Rainy

Step 5 § The ID 3 algorithm is run recursively on the nonleaf branches, until all data is classified. So, our tree looks like this… 18
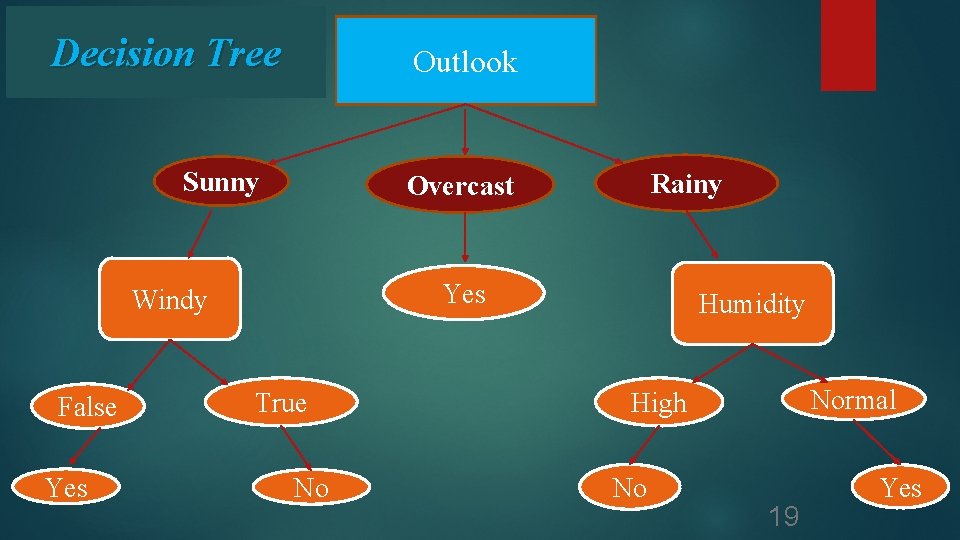
Decision Tree Outlook Sunny Yes Windy False Yes Rainy Overcast True No Humidity Normal High No 19 Yes

Naive Bayes 20 § It is a type of supervised algorithm. § It is a very simple algorithm to implement and good results have obtained in cases. § The Naïve Bayes classifier is based on Baye’s theorem and classifies every value as independence between every pair of features. § In Naïve Bayes we would guess the best class and assign a probability for that best guess. § Naïve Bayes classifiers work well in many real-world situations such as document classification and spam filtering.

Background 21

Continue…. where, c is target and x , y are attributes 22

Continue… 23

Conditional Probability Model Prior Probability Likelihood Posterior Probability Normalizing constant 24
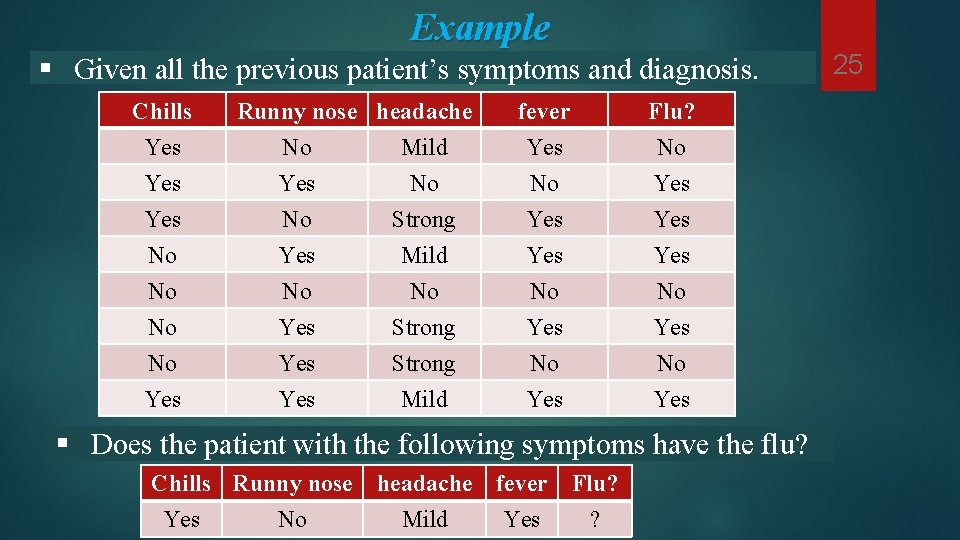
Example § Given all the previous patient’s symptoms and diagnosis. Chills Yes Yes No No Yes Runny nose headache No Mild Yes No No Strong Yes No Yes Yes Mild No Strong Mild fever Yes No Yes Flu? No Yes Yes No Yes § Does the patient with the following symptoms have the flu? Chills Runny nose headache fever Flu? Yes No Mild Yes ? 25
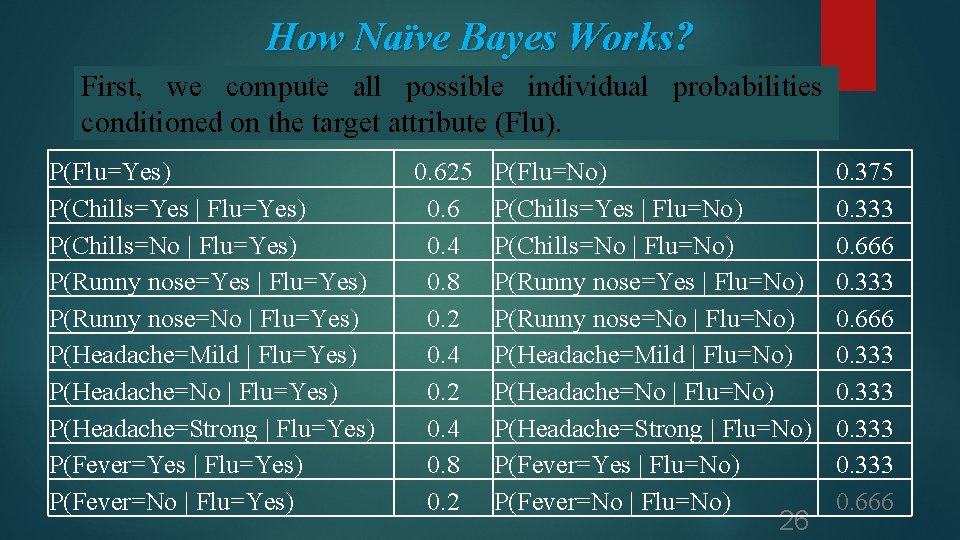
How Naïve Bayes Works? First, we compute all possible individual probabilities conditioned on the target attribute (Flu). P(Flu=Yes) P(Chills=Yes | Flu=Yes) P(Chills=No | Flu=Yes) P(Runny nose=Yes | Flu=Yes) P(Runny nose=No | Flu=Yes) P(Headache=Mild | Flu=Yes) P(Headache=No | Flu=Yes) P(Headache=Strong | Flu=Yes) P(Fever=Yes | Flu=Yes) P(Fever=No | Flu=Yes) 0. 625 0. 6 0. 4 0. 8 0. 2 P(Flu=No) P(Chills=Yes | Flu=No) P(Chills=No | Flu=No) P(Runny nose=Yes | Flu=No) P(Runny nose=No | Flu=No) P(Headache=Mild | Flu=No) P(Headache=No | Flu=No) P(Headache=Strong | Flu=No) P(Fever=Yes | Flu=No) P(Fever=No | Flu=No) 26 0. 375 0. 333 0. 666

And then decide… 27 Some Classification Algorithms in Machine Learning P(Flu=Yes | Given attribute) =P(Chills=Y | Flu=Y)*P(Runny nose=N | Flu=Y)*P(Headache=Mild | Flu=Y) *P(Fever=N | Flu=Y)*P(Flu=Y) =0. 6*0. 2*0. 4*0. 2*0. 625 =0. 006 Vs P(Flu=No | Given attribute) =P(Chills=Y | Flu=N)*P(Runny nose=N | Flu=N)*P(Headache=Mild | Flu=N) *P(Fever=N | Flu=N)*P(Flu=N) =0. 333*0. 666*0. 375 =0. 0184 So, Naïve Bayes classifier predicts that the patient doesn’t have the flu.

Applications § § § § Speech recognition Effective web search Fraud detection Medical diagnosis Stock market analysis Spam filtering Computational finance Structural health monitoring 28

Reference 29 § www. machinelearningplus. com § www. rischanlab. github. io § www. analyticsvidhya. com § www. researchgate. net § Sankara Subbu, Ramesh, "Brief Study of Classification Algorithms in Machine Learning" (2017). CUNY Academic Works. http: //academicworks. cuny. edu/cc_etds_theses/679

30 THANK YOU
- Slides: 30