Some Basic Concepts of Energy Prepared for BIOEESEGY

Some Basic Concepts of Energy Prepared for BIO/EES/EGY 105 Energy in Our World Kenneth M. Klemow, Ph. D. Wilkes University

Overview of topics Overview ◦ Energy defined ◦ Forms of energy The physical nature of energy ◦ Energy and Newtonian Laws of Motion ◦ Units of measure ◦ Conversions Terminology pertaining to energy

What is energy? Ability to do work Physicists distinguish between kinetic and potential energy Energy comes in different forms ◦ ◦ ◦ ◦ Radiation Mechanical energy Chemical energy Atomic energy Electromagnetic energy Electrical energy Heat energy

Energy relates to Newtonian motion Sir Isaac Newton 1642 - 1727

What is energy? – Physics definition Energy = Force x distance Force = Acceleration x mass Acceleration = Speed / time Speed = Distance / time

Speed - Velocity Speed = distance / time Ways of expressing ◦ ◦ Miles / hour Km / hour Feet / second Meters / second Other relationships ◦ Distance = Speed x time ◦ Time = Distance / speed Velocity is a vector: implies speed and direction

Speed: Conversions 1 ft/s = 0. 305 m/s 1 mi/h = 0. 447 m/s 1 km/hr = 0. 28 m/s

Some quick problems 1. A car drives 72 miles in 120 minutes. What is its velocity in miles per hour? 2. A person runs at 6 miles per hour. How far can that person run in 10 minutes? ◦ Expressed in miles: ◦ Expressed in feet: 3. How long does it take for that person to run 528 feet?

Solution to problem 1 1. A car drives 72 miles in 120 minutes. What is its velocity in miles per hour. Velocity = distance / time Velocity = 72 miles / 120 minutes 1 hour = 60 minutes Velocity = 72 miles / 2 hours Velocity = 36 miles / hour

Solution to problem 2 2. A person runs at 6 miles per hour. How far can that person run in 10 minutes? ◦ Expressed in miles: ◦ ◦ ◦ ◦ ◦ Velocity = distance / time Velocity x time = distance Distance = Velocity x time Distance = 6 miles per hour x 10 minutes 1 hour = 60 minutes Distance = 6 mph x 10 min x 1 h / 60 min. Distance = 6 (10/60) Distance = 60 / 60 Distance = 1 mile

Solution to problem 2 2. A person runs at 6 miles per hour. How far can that person run in 10 minutes? ◦ Expressed in feet: ◦ ◦ Distance = 1 mile 5280 feet = 1 mile Distance = 1 mile x (5280 feet / 1 mile) Distance = 5280 feet

Solution to problem 2 2. A person runs at 6 miles per hour. How far can that person run in 10 minutes? ◦ Expressed in feet: ◦ ◦ Distance = 1 mile 5280 feet = 1 mile Distance = 1 mile x (5280 feet / 1 mile) Distance = 5280 feet ◦ Thus, 5280 feet in ten minutes

Solution to problem 3 3. How long does it take for that person to run 528 feet? Time = Distance / speed Time = 528 feet / 5280 feet per mile = 0. 1 mile Time = 0. 1 mile / 6 miles per hour Time = 1/60 hours Time = 1 minute

Another problem A car is traveling 60 miles per hour. How many feet can it travel in one second?

Another problem A car is traveling 60 miles per hour. How many feet can it travel in one second? 60 mi /hr x (5280 ft/mi) x (1/3600 sec/hr) = 88 ft/sec

Acceleration = Change in velocity / time ◦ Expressed as distance / time X time ◦ Or distance / time 2 Occurs when an object is speeding up or slowing down Units include ◦ ◦ Miles / hour 2 Km / hour 2 Feet / second 2 Meters / second 2

Helpful conversions 1 ft/s 2 = 0. 305 m/s 2 1 m/s 2 = 3. 28 ft/s 2

A quick problem A Fiat 500 can accelerate to 30 km / hour in 6 seconds. What is its acceleration? ◦ Express in terms of m / second 2 (see Example 2. 2 on p. 40)

A quick problem A Fiat 500 can accelerate to 30 km / hour in 6 seconds. What is its acceleration? ◦ Express in terms of m / second 2 (see Example 2. 2 on p. 40) A = (30 km/hr) / 6 sec. A = 5 km /hr / sec 1 km/hr = 0. 28 m/s A = 5 km/hr/sec x 0. 28 m/s / km/hr A = 1. 4 m/s 2

Can calculate velocity by knowing acceleration and time Velocity = Acceleration X Time Problem: ◦ Return to the Fiat What After is velocity after 1 second? = 3 seconds? 6 seconds? 9 seconds? 12 seconds?

Can calculate velocity by knowing acceleration and time Velocity = Acceleration X Time Problem: ◦ Return to the Fiat What After is velocity after 1 second? = 1. 4 m/s 3 seconds? = 4. 2 m/s 6 seconds? = 8. 4 m/s 9 seconds? = 12. 6 m/s 12 seconds? = 16. 8 m/s

Gravity has an acceleration (Agrav) ◦ Metric: 9. 8 m/s 2 ◦ English: 32 ft/s 2

Can calculate distance moved as a function of acceleration and time X = (1/2) x A x T 2 (see p. 62 of text for derivation) Problem: Imagine you drop a stone from a cliff, and it takes three seconds to hit the water below. How high was the cliff above the water? How fast was the stone moving when it hit the water?

Can calculate distance moved as a function of acceleration and time X = (1/2) x A x T 2 (see p. 62 of text for derivation) Problem: Imagine you drop a stone from a cliff, and it takes three seconds to hit the water below. How high was the cliff above the water? X = (1/2) x 9. 8 m/s 2 x 3 s. X = 4. 9 m/s 2 x 9 s 2 X = 44. 1 m How fast was the stone moving when it hit the water? V=Ax. T V = 9. 8 m/s 2 x 3 s = 29. 4 m/s

Momentum and Force Momentum = mass x velocity Force = mass x acceleration Common unit of measure force: ◦ Newton (N = kg x m / s²) Other relationships ◦ Mass = Force / acceleration (kg=F/a) ◦ Acceleration = Force / mass (A=F/kg)

Sample problem A rock having a mass of 2 kg falls into the water from a cliff. What is the force that it exerts? ◦ F = Kg x A ◦ F = 2 Kg x 9. 8 m / s 2 ◦ F = 19. 6 Kg x m /s 2 ◦ Does that force vary if the cliff is 50’ high, as opposed to being 100’ high?

Mass and Weight are sometimes confused. Mass is a property of a body (measure of inertia). ◦ Irrespective of its position relative to gravity. ◦ Often expressed as Kg. Weight depends on gravity. An object will weigh more on earth than on moon because gravitational force greater on earth. ◦ Weight often considered to be unit of force, expressed as Kg x Agrav Where Kg is mass and Agrav is acceleration due to gravity.

Newton’s Laws of Motion 1. A body will continue to remain at rest or in motion with a constant velocity unless it is acted upon by an outside force. 2. The acceleration of an object is directly proportional to the net force acting on it, and is inversely proportional to its mass (A = F/Kg). 3. For every action force, there is an equal and opposite reaction force.

Energy (work) Energy = Force x Distance ◦ Joule (J) = Newton x meter Energy of an apple 1 m from the floor ◦ Some additional measures of energy Foot pound = 1. 4 J 1 calorie = 4. 187 J 1 BTU = 1054 J

Energy can be potential or kinetic Potential energy ◦ Stored energy, able to do work if released. Examples include: Objects placed at an elevation Water behind dam Release energy if they fall Objects placed at mechanical tension Wound up spring Release energy if tension is relieved Chemical bond energy Organic molecules Energy released if combusted ◦ Potential energy due to elevation PEG = weight x height = Kg x Agrav x h

Energy can be potential or kinetic Kinetic energy ◦ Energy of motion Examples include: Moving water Moving catapult ◦ Can be expressed mathematically as 1/2 Kg x v 2

Power Rate at which energy is produced, used, or transferred. ◦ Expressed as energy per time ◦ Common units include Watt (J / s) Ft-lb / sec Horsepower 1 hp = 550 ft-lbs / sec 1 hp = 746 Watts

Common unit is kilowatt hour Question: A kilowatt hour is a measure of: ◦ ◦ ◦ Power Energy Force Acceleration None of the above

Energy and power Power = energy / time Energy = power x time www. belmont. k 12. ca. us

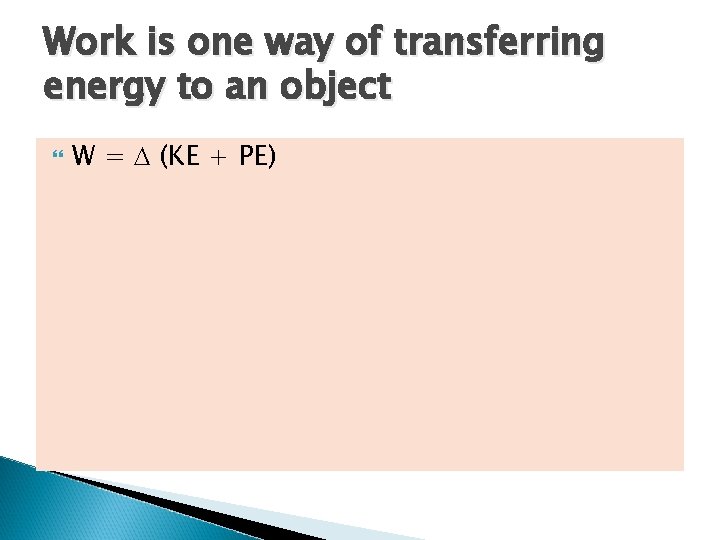
Work is one way of transferring energy to an object W = D (KE + PE)

“Conversion” and “conservation” two important concepts Both have two meanings ◦ Conversion Translating between different units of measure Joule <-> Calorie <-> BTU Changing from one form to another Chemical energy -> Thermal energy ◦ Conservation First law of thermodynamics Energy cannot be created or destroyed, only converted Reduce wasteful energy consumption Switch from incandescent to light-emitting diode (LED)

Some conversion factors (See Table 3. 4 on pp. 86 – 87 for more complete list) 1 1 1 kilowatt hour = 3. 60 x 106 J barrel oil equivalent = 6. 119 x 109 J ton wood equivalent = 9. 83 x 109 J ton coal equivalent = 29. 31 x 109 J ton oil equivalent = 41. 87 x 109 J quad (PBtu) = 1. 055 x 1018 J

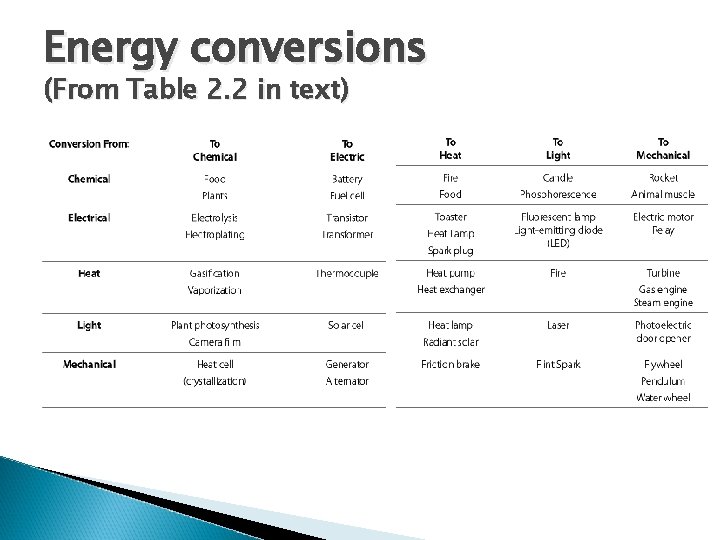
Energy conversions (From Table 2. 2 in text)

Laws of Thermodyamics First law: Energy cannot be created nor destroyed, can only be converted (conservation of energy) ◦ In an isolated system, total energy will always remain constant Second law: No energy conversion is perfect; always get some loss as heat. ◦ Gives direction to a reaction ◦ Get increase in disorder (entropy).

Consequences of Second Law In system involving movement, always get loss as friction Thus perpetual motion machines are impossible (yet people still try to invent them) Waste heat given off to environment ◦ Ultimately go off to space

Efficiency an important measure Efficiency = energy (work) output X 100 total energy input • Efficiencies can vary from 5% - 95% • In multistep processes, efficiency is the product of efficiency of each step. • Comparative assessments of energy processes / devices typically take great pains to accurately measure efficiency

Efficiencies of energy conversion devices and systems Electric generators Electric motor Gas furnace Wind turbine Fossil fuel power plant Nuclear power plant Automobile engine LED lamp Fluorescent lamp Incandescent lamp 70 -99% 50 -90% 70 -90% 35 -50% 35 -40% 30 -35% 20 -30% 25 -30% 20% 5% From Table 3. 1 on p. 78 of text

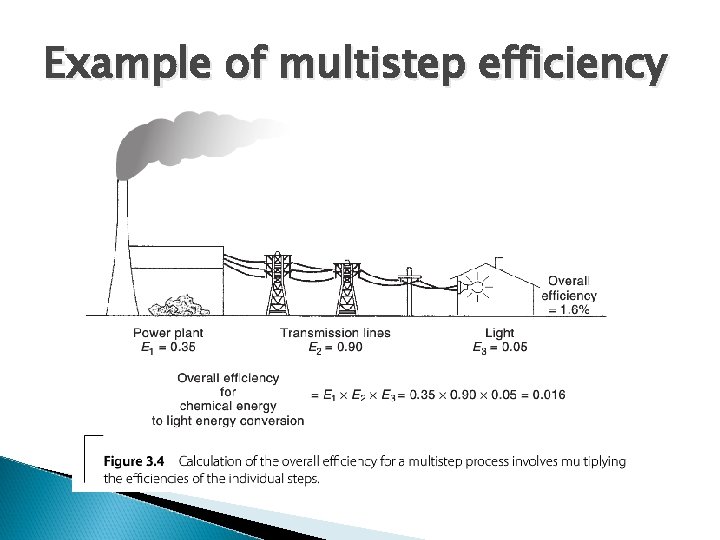
Example of multistep efficiency

What would be the efficiency of the following process? Nuclear power plant -> Wires -> LED bulb

What would be the efficiency of the following process? Nuclear power plant -> Wires -> LED bulb 0. 35 0. 90 0. 30

What would be the efficiency of the following process? Nuclear power plant -> Wires -> LED bulb 0. 35 0. 90 0. 30 Efficiency = 9. 45%