Solving TwoStep and Solving TwoStep 1 4 MultiStep




































- Slides: 36

Solving Two-Step and Solving Two-Step 1 -4 Multi-Step Equations Warm Up Lesson Presentation Lesson Quiz Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Objective Solve equations in one variable that contain more than one operation. Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Example 1 A: Solving Two-Step Equations Solve 18 = 4 a + 10 – 10 8 = 4 a 4 4 2=a Holt Mc. Dougal Algebra 1 First a is multiplied by 4. Then 10 is added. Work backward: Subtract 10 from both sides. Since a is multiplied by 4, divide both sides by 4 to undo the multiplication.

Solving Two-Step and 1 -4 Multi-Step Equations Example 1 B: Solving Two-Step Equations Solve 5 t – 2 = – 32 +2 +2 5 t = – 30 5 5 t = – 6 Holt Mc. Dougal Algebra 1 First t is multiplied by 5. Then 2 is subtracted. Work backward: Add 2 to both sides. Since t is multiplied by 5, divide both sides by 5 to undo the multiplication.

Solving Two-Step and 1 -4 Multi-Step Equations Check it Out! Example 1 a Solve – 4 + 7 x = 3 +4 +4 7 x = 7 7 7 x=1 Holt Mc. Dougal Algebra 1 First x is multiplied by 7. Then – 4 is added. Work backward: Add 4 to both sides. Since x is multiplied by 7, divide both sides by 7 to undo the multiplication.

Solving Two-Step and 1 -4 Multi-Step Equations Check it Out! Example 1 b Solve 1. 5 = 1. 2 y – 5. 7 First y is multiplied by 1. 2. Then 5. 7 is subtracted. Work backward: Add 5. 7 + 5. 7 to both sides. 7. 2 = 1. 2 y Since y is multiplied by 1. 2, divide both 7. 2 = 1. 2 y sides by 1. 2 to undo the 1. 2 multiplication. 6=y Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Check it Out! Example 1 c Solve . – 2 First n is divided by 7. Then 2 is added. Work backward: Subtract 2 from both sides. Since n is divided by 7, multiply both sides by 7 to undo the division. n=0 Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Example 2 A: Solving Two-Step Equations That Contain Fractions Solve . Method 1 Use fraction operations. y 3 3 Since 4 is subtracted from 8 , add 4 to both sides to undo the subtraction. Since y is divided by 8, multiply both sides by 8 to undo the division. Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Example 2 A Continued Solve . Method 1 Use fraction operations. Simplify. Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Example 2 A Continued Solve . Method 2 Multiply by the LCD to clear the fractions. Multiply both sides by 24, the LCD of the fractions. Distribute 24 on the left side. 3 y – 18 = 14 +18 3 y = 32 Holt Mc. Dougal Algebra 1 Simplify. Since 18 is subtracted from 3 y, add 18 to both sides to undo the subtraction.

Solving Two-Step and 1 -4 Multi-Step Equations Example 2 A Continued Solve . Method 2 Multiply by the LCD to clear the fractions. Since y is multiplied by 3, divide 3 y = 32 both sides by 3 to undo the 3 3 multiplication. Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Example 2 B: Solving Two-Step Equations That Contain Fractions Solve . Method 1 Use fraction operations. 3 Since 3 is added to 2 r, subtract 4 4 3 from both sides to undo the addition. 2 3 The reciprocal of 3 is 2. Since r is 2 multiplied by , multiply both sides 3 3 by Holt Mc. Dougal Algebra 1 2 .

Solving Two-Step and 1 -4 Multi-Step Equations Example 2 B Continued Solve . Method 1 Use fraction operations. Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Example 2 B Continued Solve . Method 2 Multiply by the LCD to clear the fractions. Multiply both sides by 12, the LCD of the fractions. Distribute 12 on the left side. 8 r + 9 = 7 – 9 8 r = – 2 Holt Mc. Dougal Algebra 1 Simplify. Since 9 is added to 8 r, subtract 9 from both sides to undo the addition.

Solving Two-Step and 1 -4 Multi-Step Equations Example 2 B Continued Solve . Method 2 Multiply by the LCD to clear the fractions. 8 r = – 2 8 8 Holt Mc. Dougal Algebra 1 Since r is multiplied by 8, divide both sides by 8 to undo the multiplication.

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 2 a Solve . Method 2 Multiply by the LCD to clear the fractions. Multiply both sides by 10, the LCD of the fractions. Distribute 10 on the left side. 4 x – 5 = 50 +5 +5 4 x = 55 Holt Mc. Dougal Algebra 1 Simplify. Since 5 is subtracted from 4 x, add 5 to both sides to undo the subtraction.

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 2 a Solve . Method 2 Multiply by the LCD to clear the fractions. 4 x = 55 4 4 Holt Mc. Dougal Algebra 1 Simplify. Since 4 is multiplied by x, divide both sides by 4 to undo the multiplication.

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 2 b Solve . Method 2 Multiply by the LCD to clear the fractions. Multiply both sides by 8, the LCD of the fractions. Distribute 8 on the left side. 6 u + 4 = 7 4 4 6 u = 3 Holt Mc. Dougal Algebra 1 Simplify. Since 4 is added to 6 u, subtract 4 from both sides to undo the addition.

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 2 b Continued Solve . Method 2 Multiply by the LCD to clear the fractions. 6 u = 3 6 6 Holt Mc. Dougal Algebra 1 Since u is multiplied by 6, divide both sides by 6 to undo the multiplication.

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 2 c Solve . Method 1 Use fraction operations. n 1 1 Since 3 is subtracted from 5 , add 3 to both sides to undo the subtraction. Simplify. Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 2 c Continued Solve . Method 1 Use fraction operations. Since n is divided by 5, multiply both sides by 5 to undo the division. n = 15 Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Example 3 A: Simplifying Before Solving Equations Solve 8 x – 21 + 5 x = – 15. 8 x – 21 – 5 x = – 15 8 x – 5 x – 21 = – 15 Use the Commutative Property of Addition. 3 x – 21 = – 15 Combine like terms. + 21 +21 Since 21 is subtracted from 3 x, add 21 to both sides to undo the subtraction. 3 x = 6 Since x is multiplied by 3, divide both sides by 3 to undo the multiplication. x=2 Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Example 3 B: Simplifying Before Solving Equations Solve 10 y – (4 y + 8) = – 20 10 y + (– 1)(4 y + 8) = – 20 Write subtraction as addition of the opposite. 10 y + (– 1)(4 y) + (– 1)( 8) = – 20 Distribute – 1 on the left side. 10 y – 4 y – 8 = – 20 Simplify. 6 y – 8 = – 20 Combine like terms. +8 + 8 Since 8 is subtracted from 6 y, add 8 to both sides to undo 6 y = – 12 6 6 y = – 2 Holt Mc. Dougal Algebra 1 the subtraction. Since y is multiplied by 6, divide both sides by 6 to undo the multiplication.

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 3 a Solve 2 a + 3 – 8 a = 8 2 a – 8 a + 3 = 8 – 6 a + 3 = 8 – 3 – 6 a = 5 Use the Commutative Property of Addition. Combine like terms. Since 3 is added to – 6 a, subtract 3 from both sides to undo the addition. Since a is multiplied by – 6, divide both sides by – 6 to undo the multiplication. Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 3 b Solve – 2(3 – d) = 4 (– 2)(3) + (– 2)(–d) = 4 – 6 + 2 d = 4 +6 +6 2 d = 10 2 2 d=5 Holt Mc. Dougal Algebra 1 Distribute – 2 on the left side. Simplify. Add 6 to both sides. Since d is multiplied by 2, divide both sides by 2 to undo the multiplication.

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 3 c Solve 4(x – 2) + 2 x = 40 (4)(x) + (4)(– 2) + 2 x = 40 4 x – 8 + 2 x = 40 4 x + 2 x – 8 6 x – 8 +8 6 x = 40 +8 = 48 6 x = 48 6 6 x=8 Holt Mc. Dougal Algebra 1 Distribute 4 on the left side. Simplify. Commutative Property of Addition. Combine like terms. Since 8 is subtracted from 6 x, add 8 to both sides to undo the subtraction. Since x is multiplied by 6, divide both sides by 6 to undo the multiplication.

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 4 Sara paid $15. 95 to become a member at a gym. She then paid a monthly membership fee. Her total cost for 12 months was $735. 95. How much was the monthly fee? Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 4 Continued 1 Understand the Problem The answer will the monthly membership fee. List the important information: • Sara paid $15. 95 to become a gym member. • Sara pays a monthly membership fee. • Her total cost for 12 months was $735. 95. Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations 2 Check It Out! Example 4 Continued Make a Plan Let m represent the monthly membership fee that Sara must pay. That means that Sara must pay 12 m. However, Sara must also add the amount she spent to become a gym member. total cost monthly = fee 735. 95 = Holt Mc. Dougal Algebra 1 12 m initial + membership + 15. 95

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 4 Continued 3 Solve 735. 95 = 12 m + 15. 95 Since 15. 95 is added to 12 m, subtract 15. 95 from both – 15. 95 sides to undo the addition. 720 = 12 m 12 12 60 = m Holt Mc. Dougal Algebra 1 Since m is multiplied by 12, divide both sides by 12 to undo the multiplication.

Solving Two-Step and 1 -4 Multi-Step Equations Check It Out! Example 4 Continued 4 Look Back Check that the answer is reasonable. Sara pays $60 a month, so after 12 months Sara has paid 12(60) = 720. Add the cost of the initial membership fee, which is about $16. So the total paid is about $736, which is close to the amount given in the problem, $735. 95. Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Example 5 A: Solving Equations to Find an Indicated Value If 4 a + 0. 2 = 5, find the value of a – 1. Step 1 Find the value of a. 4 a + 0. 2 = 5 Since 0. 2 is added to 4 a, subtract 0. 2 – 0. 2 from both sides to undo the addition. 4 a = 4. 8 Since a is multiplied by 4, divide both sides by 4 to undo the multiplication. a = 1. 2 Step 2 Find the value of a – 1. 1. 2 – 1 To find the value of a – 1, substitute 1. 2 for a. Simplify. 0. 2 Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Example 5 B: Solving Equations to Find an Indicated Value If 3 d – (9 – 2 d) = 51, find the value of 3 d. Step 1 Find the value of d. 3 d – (9 – 2 d) = 51 3 d – 9 + 2 d = 51 5 d – 9 = 51 +9 +9 Since 9 is subtracted from 5 d, add 9 to both sides to undo the subtraction. 5 d = 60 Since d is multiplied by 5, divide both sides by 5 to undo the multiplication. d = 12 Holt Mc. Dougal Algebra 1

Solving Two-Step and 1 -4 Multi-Step Equations Example 5 B Continued If 3 d – (9 – 2 d) = 51, find the value of 3 d. Step 2 Find the value of 3 d. d = 12 3(12) 36 Holt Mc. Dougal Algebra 1 To find the value of 3 d, substitute 12 for d. Simplify.

Solving Two-Step and 1 -4 Multi-Step Equations Lesson Quiz: Part 1 Solve each equation. 1. 4 y + 8 = 2 – 8 2. 3. 2 y + 29 – 8 y = 5 4 4. 3(x – 9) = 30 19 5. x – (12 – x) = 38 6. 9 Holt Mc. Dougal Algebra 1 25

Solving Two-Step and 1 -4 Multi-Step Equations Lesson Quiz: Part 2 7. If 3 b – (6 – b) = – 22, find the value of 7 b. – 28 8. Josie bought 4 cases of sports drinks for an upcoming meet. After talking to her coach, she bought 3 more cases and spent an additional $6. 95 on other items. Her receipts totaled $74. 15. Write and solve an equation to find how much each case of sports drinks cost. 4 c + 3 c + 6. 95 = 74. 15; $9. 60 Holt Mc. Dougal Algebra 1
 List of goals to set for yourself
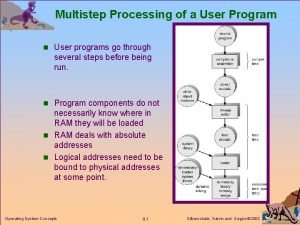
List of goals to set for yourself Multistep processing of a user program
Multistep processing of a user program Ras oncogene
Ras oncogene Clausola multistep
Clausola multistep Unit 4 solving quadratic equations
Unit 4 solving quadratic equations Solving systems using tables and graphs
Solving systems using tables and graphs How to solve square root equations
How to solve square root equations How to solve rational equations and inequalities
How to solve rational equations and inequalities Solve the rational equation 8/x+1/5=3/x
Solve the rational equation 8/x+1/5=3/x 5-5 solving rational equations and inequalities
5-5 solving rational equations and inequalities Inequalities with radicals
Inequalities with radicals Solving radical inequalities
Solving radical inequalities Anya is drawing a circle graph
Anya is drawing a circle graph Solving multi step equations and inequalities
Solving multi step equations and inequalities Solving and graphing inequalities on a number line
Solving and graphing inequalities on a number line Solving equations using addition and subtraction
Solving equations using addition and subtraction Best books on problem solving and decision making
Best books on problem solving and decision making One step equations multiplication
One step equations multiplication Forming and solving equations worksheet
Forming and solving equations worksheet Forming and solving equations worksheet
Forming and solving equations worksheet Problem solving
Problem solving Writing inequalities worksheet
Writing inequalities worksheet Solving equations and inequalities
Solving equations and inequalities Solving equations and inequalities
Solving equations and inequalities Chapter 4: exponential and logarithmic functions answer key
Chapter 4: exponential and logarithmic functions answer key Solving problems analytically
Solving problems analytically Solving addition and subtraction equations answers
Solving addition and subtraction equations answers Solving radical equations and inequalities
Solving radical equations and inequalities 8-5 solving rational equations and inequalities
8-5 solving rational equations and inequalities Factoring and solving polynomial equations
Factoring and solving polynomial equations Exponential and logarithmic inequalities
Exponential and logarithmic inequalities 4-1 classifying triangles
4-1 classifying triangles 1-3 solving equations
1-3 solving equations Teamwork problem solving
Teamwork problem solving Two step inequalities
Two step inequalities Solving square root and other radical equations
Solving square root and other radical equations 5-5 solving rational equations and inequalities
5-5 solving rational equations and inequalities