Solving The Nonlinear Equations Through The Muller Method

Solving The Nonlinear Equations Through The Muller Method. Sung-Ju Kang Department Of Physics Kangwon National University Muller’s method can be used for any root-finding problem, but it is particularly useful for approximation the roots of polynomials. This technique is an iterative method that requires three starting values (xi, f(xi)), (x i-1, f(x i-1)), (x i-2, f(x i-2)).

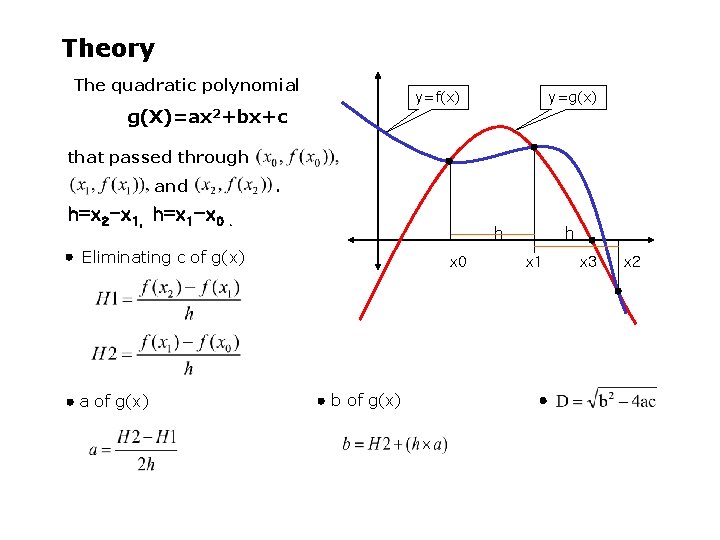
Theory The quadratic polynomial y=f(x) g(X)=ax 2+bx+c y=g(x) that passed through and . h=x 2 -x 1, h=x 1 -x 0. h Eliminating c of g(x) a of g(x) x 0 b of g(x) h x 1 x 3 x 2

To determine x 3 , a zero of P, we apply the quadratic formula to We apply the formula in the manner prescribed, The result in x 3 being selected as the closest zero of P to x 2. And then x 0 = x 1, and h = x 3 – x 1. Once x 3 is determined, the procedure is reinitialized using x 0, x 1, and x 3 in place of x 0, x 1, and x 2 to determine the next approximation, x 4. -- At each step, the involves the radical approximate complex roots when . so the method gives .

Algorism INPUT function ; tolerance OUTPUT Step 1 initial approximations tol ; h; approximation x do { Step 2 set Step 3 set if b > 0 Step 4 set Step 5 set while( |h| > tol ); Step 6 x 1 ; OUTPUT ( Result STOP. x) constant a; b; D; than set E = b+D else set E = b-D. }

Programming with C language #include<stdio. h> do { #include<math. h> H 2=(f 1 -f 0)/h; a=(H 2 -H 1)/(2*h); double f, X, tol; H 1=H 2; double F(double X); b=H 2+a*h; double M(double x 1); if(D>=0) D=sqrt(D); D=b*b-4. 0*f 1*a; if (b>=0) E=b+D; else E=b-D; void main(){ h=-2. 0*f 1/E; double x 1; f 0=f 1; X=X+h; tol=0. 000001; f 1=F(X); f 2=(f 1 -f 0)/h; x 1 = 3. 0; printf("t%fn", h); X=M(x 1); } while(fabs(h)>=tol); printf("tx = %f", X); } return (X); } double M(double x 1){ double x 0, x 2, xc, h, f 0, f 1, f 2, H 1, H 2, a, b, D, E; double F(double X) h=1. 0; { x 2=x 1+h; f 2=F(x 2); f=pow(X, 5)-2*pow(X, 4)+4*pow(X, 3)-8*X*X+4*X-8; x 0=x 1 -h; f 0=F(x 0); return f; H 1=(f 2 -f 1)/h; xc=x 1; f 1=F(xc); X=xc; }