Solving the groundwater flow equation R Rossetto rudy

Solving the groundwater flow equation R. Rossetto rudy. rossetto@sssup. it

Solving groundwater flow equation/1 A numerical model is made up of a set of equations, which approximate the partial differential equation, boundary conditions specifing the hydrodynamics at the boundaries of my investigated domain and the initial conditions within my domain The finite-difference method, FDM, and the finite-element method, FEM, are the most used techniques to solve the groundwater flow equation.

Solving groundwater flow equation/2 Let’s consider a confined aquifer homogeneous and isotropic. Let’s suppose this aquifer is connected on two sides by two different lakes. In this case the groundwater flow equation reduces to flow in only one dimension. That is: h=10 m h=0 m The approximate solution is: hxm=(1/2)(hx-1 m+hx+1 m-1) Where m is the number of the iteration. hx-1 hx hx+1

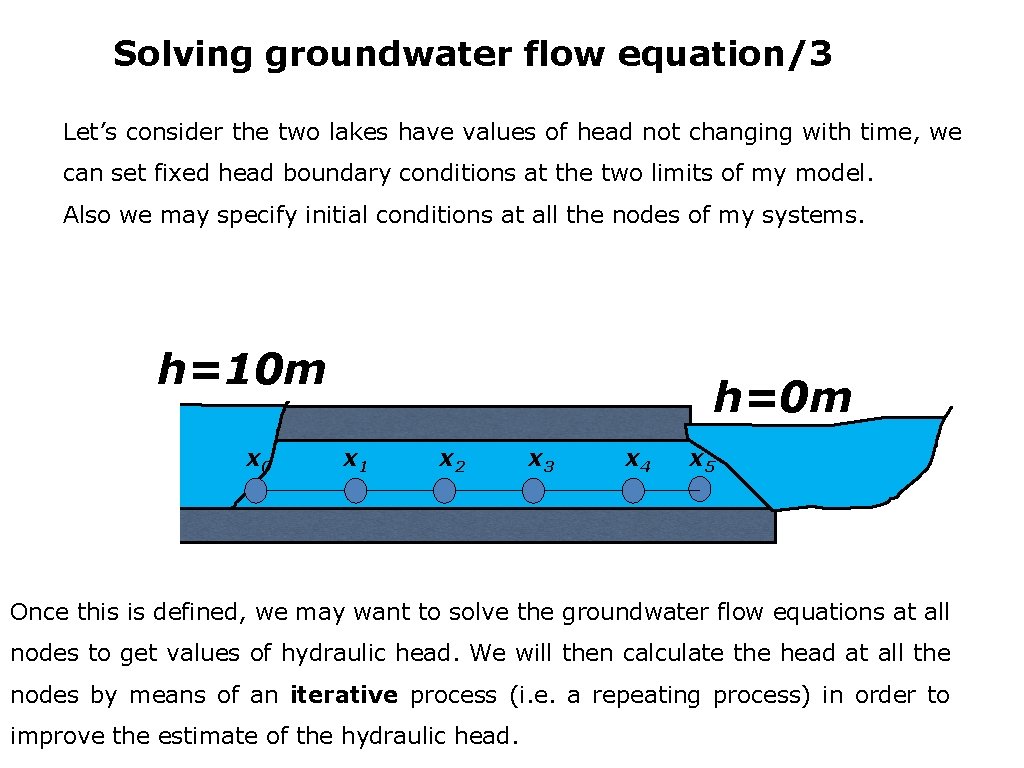
Solving groundwater flow equation/3 Let’s consider the two lakes have values of head not changing with time, we can set fixed head boundary conditions at the two limits of my model. Also we may specify initial conditions at all the nodes of my systems. h=10 m x 0 h=0 m x 1 x 2 x 3 x 4 x 5 Once this is defined, we may want to solve the groundwater flow equations at all nodes to get values of hydraulic head. We will then calculate the head at all the nodes by means of an iterative process (i. e. a repeating process) in order to improve the estimate of the hydraulic head.

Solving groundwater flow equation/4 If we go for a more complex model (i. e 3 d), once we implemented the model geometry, assigned hydrodynamics parameters, boundary and initial conditions, we may resume the process of solving the groundwater flow partial differential equation in the following steps: 1 – approximate the groundwater flow equation; 2 – define when we wish the iterative process to stop, that is when our model will converge. We will have then to set a criteria for this to happen. This is usually defined by means of a head change criterion for convergence. This consists in defining a value of the difference of the hydraulic head at each node in two consecutive iterations that WE WISH is reached to terminate the process;

Solving groundwater flow equation/5 3 - solving the approximate form of the groundwater flow equation following an iterative process ; 4 - this process will then continue until at each node, the head difference at two consecutive iterations is less than the convercenge criteria set. When this is reached at each cell of my domain the solution process based on iterations will stop.

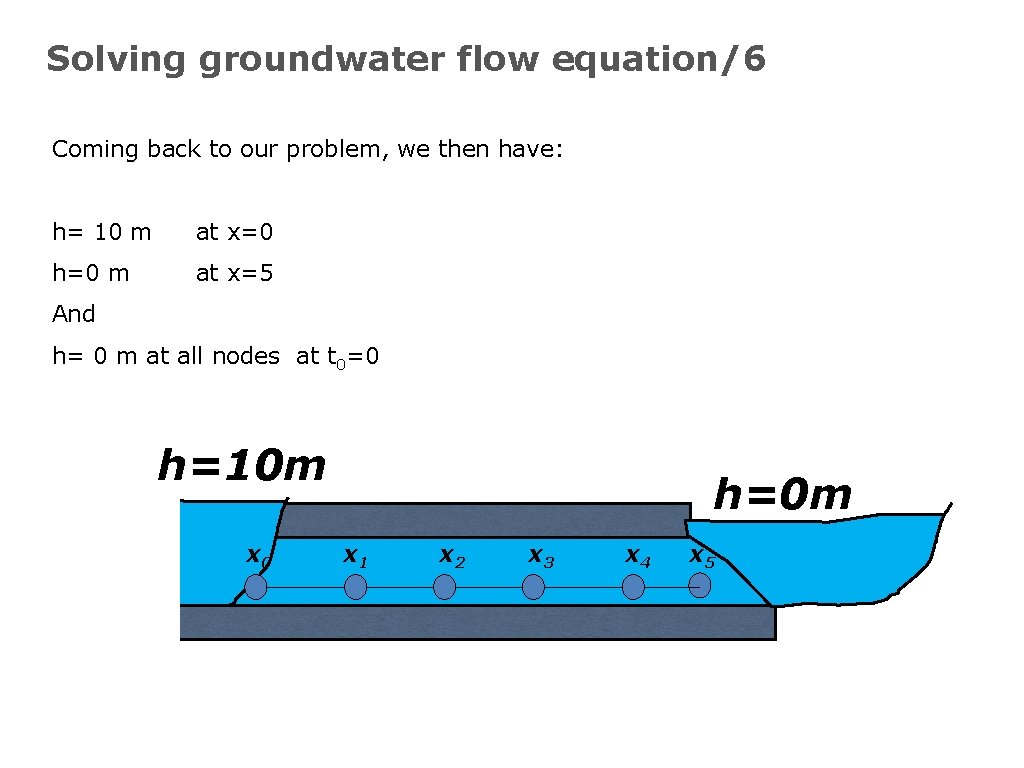
Solving groundwater flow equation/6 Coming back to our problem, we then have: h= 10 m at x=0 h=0 m at x=5 And h= 0 m at all nodes at t 0=0 h=10 m x 0 h=0 m x 1 x 2 x 3 x 4 x 5

Solving groundwater flow equation/7 Hydraulic head at node 1 in the first iteration is: h 1 m=(1/2)(h 0 m+h 2 m-1) h 1 m=(1/2)(10+0)=5. 0 m Hydraulic head at node 2 in the second iteration is: m m m-1 h 2 =(1/2)(h 1 +h 3 ) h 2 m=(1/2)(5+0)=2. 5 m Calculation at node 2 is done by using the hydraulic head calculated at node 1.

Exercise 1 Let’s use a simple spreadsheet for simulating the head in the aforementioned situation. In how many iterations does your model converge if the convergence criteria (cc) is set to 10 -2 m? How many if cc is 10 -3 m?