Solving the differential equation by using the RungeKuttas

Solving the differential equation by using the Runge-Kutta's method of order 2 Youngnam Kim 1

• Runge-Kutta’s method of order 2 This routine solve the initial value problem at equidistant points The function f(x, t) is continuous on the interval . 2

Algorithm Runge-Kutta’s method of order 2 to solve a first-order differential equation 3

Source Program • Runge-Kutta’s method of order 2 to solve a differential equation. /*Runge-Kutta's method of order 2 to solve a first-order differential equation*/ /* Solve the system of single harmonic oscillator */ /* Include header files */ #include <stdio. h> #include <math. h> #include <conio. h> #include <stdlib. h> #define w 2 /* Define constant */ float t, h, x, v, SN, PT; char FOUTN[20]; FILE *FOUT; /* Define global variables */ void RK 2(); /* General routine */ /* Sub function */ float F(float V); /* F=x'=dx/dt=v */ float G(float X); /* G=x"=dv/dt=-w*w*x */ /* Main routine */ void main(){ int i, x 0, v 0, t 0; /* Define local variable */ printf("Solveing the system of single harmonic oscillatornby using 2 nd orders Runge-Kutta's Methodnn"); printf("Number of steps = 100n. Plotting times = 50n. Step size=0. 01nw=2nn"); printf("INPUT THE OUTPUT FILE NAME. n"); scanf("%s", FOUTN); if((FOUT=fopen(FOUTN, "w"))==NULL){ printf("FILE OPEN ERROR. . . n"); getch(); exit(-1); } /* Input the values of variables */ SN=100; h=1/SN; PT=50; x 0=10; v 0=0; t 0=0; x=x 0; v=v 0; t=t 0; for(i=0; i<=SN*PT; i++){ printf("t= %10. 5 f x= %10. 5 f v=%10. 5 fn", t, x, v); fprintf(FOUT, "t= %10. 5 f x= %10. 5 f v=%10. 5 fn", t, x, v); RK 2(); } fclose(FOUT); getch(); } /* Runge-Kutta's method of order 2 */ void RK 2(){ float ti, xi, vi, f 1, f 2, g 1, g 2; /* Define local variable */ ti=t; xi=x; vi=v; f 1=F(v); g 1=G(x); x=xi+h*f 1; v=vi+h*g 1; t=ti+h; f 2=F(v); g 2=G(x); x=xi+h*(f 1+f 2)/2; v=vi+h*(g 1+g 2)/2; } float F(float V){ /* dx/dt=F(x(t), v(t), t)=v */ float f; f=V; return f; } float G(float X){ /* dv/dt=G(v(t), t)=-w*w*x */ float g; g=-w*w*X; return g; } 4

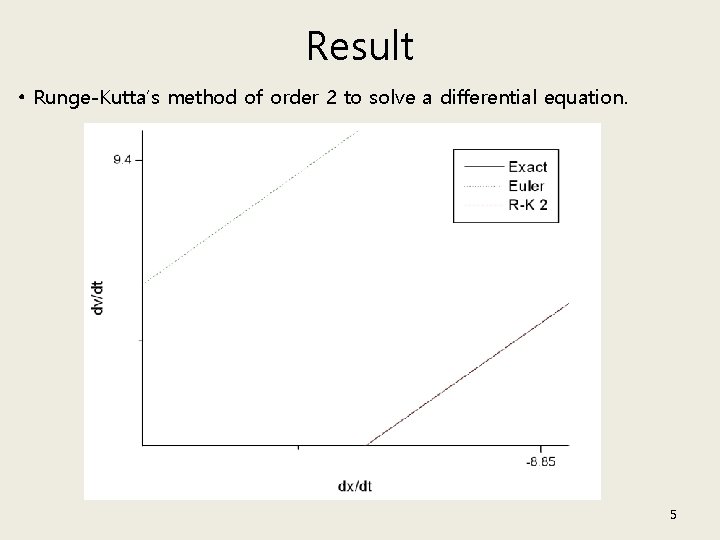
Result • Runge-Kutta’s method of order 2 to solve a differential equation. 5