Solving Systems Using Elimination Lesson 7 3 Algebra

Solving Systems Using Elimination Lesson 7 -3 Algebra 1 Additional Examples Solve by elimination. – 2 x + 9 y = 1 2 x + 3 y = 11 Step 1: Eliminate x because the sum of the coefficients is 0. 2 x + 3 y = 11 – 2 x + 9 y =1 0 + 12 y = 12 Addition Property of Equality y=1 Solve for y. Step 2: Solve for the eliminated variable x using either original equation. 2 x + 3 y = 11 2 x + 3(1) = 11 2 x + 3 = 11 2 x = 8 x=4 Choose the first equation. Substitute 1 for y. Solve for x.

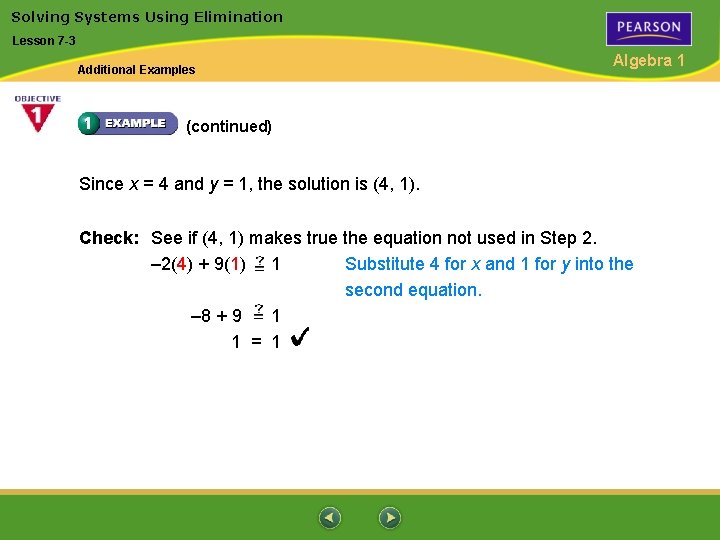
Solving Systems Using Elimination Lesson 7 -3 Additional Examples Algebra 1 (continued) Since x = 4 and y = 1, the solution is (4, 1). Check: See if (4, 1) makes true the equation not used in Step 2. – 2(4) + 9(1) 1 Substitute 4 for x and 1 for y into the second equation. – 8 + 9 1 1 = 1

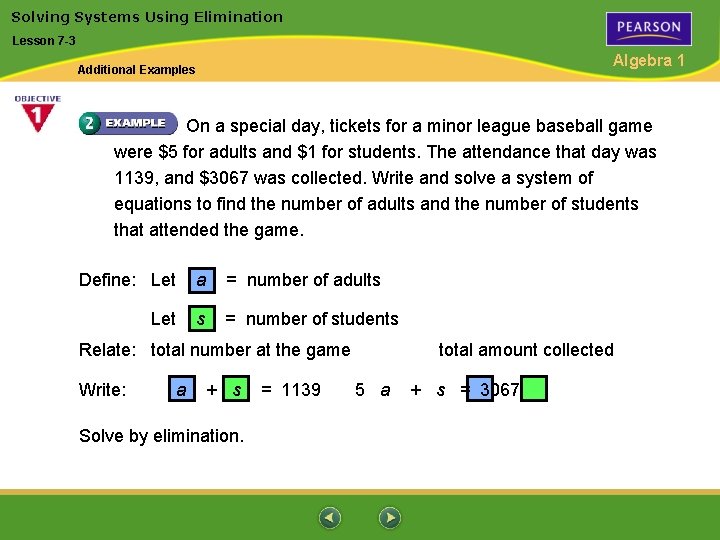
Solving Systems Using Elimination Lesson 7 -3 Algebra 1 Additional Examples On a special day, tickets for a minor league baseball game were $5 for adults and $1 for students. The attendance that day was 1139, and $3067 was collected. Write and solve a system of equations to find the number of adults and the number of students that attended the game. Define: Let a = number of adults Let s = number of students Relate: total number at the game Write: a + s Solve by elimination. = 1139 total amount collected 5 a + s = 3067

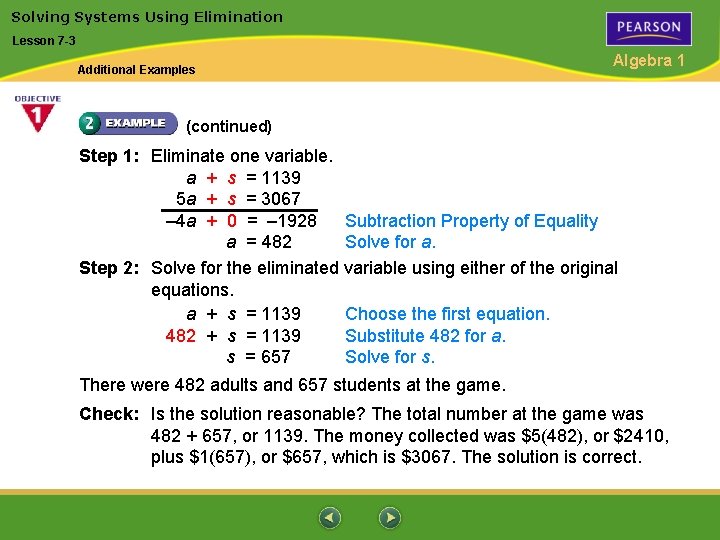
Solving Systems Using Elimination Lesson 7 -3 Additional Examples Algebra 1 (continued) Step 1: Eliminate one variable. a + s = 1139 5 a + s = 3067 – 4 a + 0 = – 1928 Subtraction Property of Equality a = 482 Solve for a. Step 2: Solve for the eliminated variable using either of the original equations. a + s = 1139 Choose the first equation. 482 + s = 1139 Substitute 482 for a. s = 657 Solve for s. There were 482 adults and 657 students at the game. Check: Is the solution reasonable? The total number at the game was 482 + 657, or 1139. The money collected was $5(482), or $2410, plus $1(657), or $657, which is $3067. The solution is correct.

Solving Systems Using Elimination Lesson 7 -3 Algebra 1 Additional Examples Solve by elimination. – 5 x – 2 y = – 14 3 x + 6 y = – 6 Step 1: Eliminate one variable. Start with the given system. 3 x + 6 y = – 6 – 5 x – 2 y = – 14 Step 2: Solve for x. – 12 x = 48 x= 4 To prepare to eliminate y, multiply the second equation by 3. 3 x + 6 y = – 6 3(– 5 x – 2 y = – 14) Add the equations to eliminate y. 3 x + 6 y = – 6 – 15 x – 6 y = – 42 – 12 x – 0 = – 48

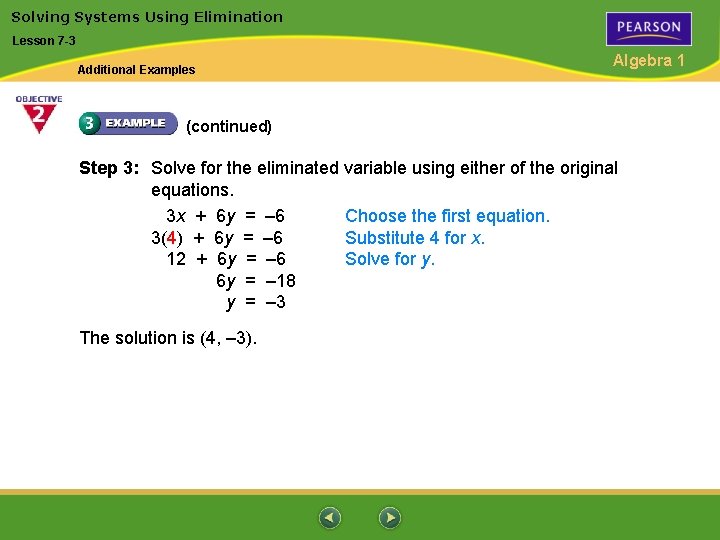
Solving Systems Using Elimination Lesson 7 -3 Additional Examples Algebra 1 (continued) Step 3: Solve for the eliminated variable using either of the original equations. 3 x + 6 y = – 6 Choose the first equation. 3(4) + 6 y = – 6 Substitute 4 for x. 12 + 6 y = – 6 Solve for y. 6 y = – 18 y = – 3 The solution is (4, – 3).

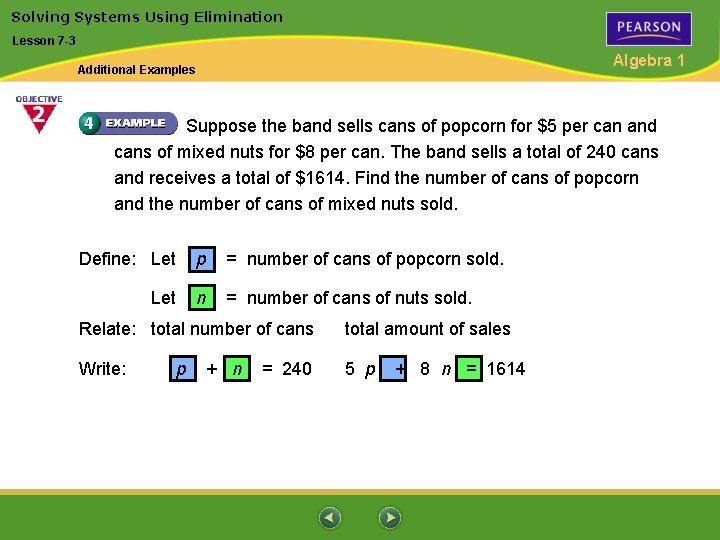
Solving Systems Using Elimination Lesson 7 -3 Algebra 1 Additional Examples Suppose the band sells cans of popcorn for $5 per can and cans of mixed nuts for $8 per can. The band sells a total of 240 cans and receives a total of $1614. Find the number of cans of popcorn and the number of cans of mixed nuts sold. Define: Let p = number of cans of popcorn sold. Let n = number of cans of nuts sold. Relate: total number of cans total amount of sales Write: 5 p p + n = 240 + 8 n = 1614

Solving Systems Using Elimination Lesson 7 -3 Algebra 1 Additional Examples (continued) Step 1: Eliminate one variable. Start with the given system. p + n = 240 5 p + 8 n = 1614 Step 2: Solve for n. – 3 n = – 414 n = 138 To prepare to eliminate p, multiply the first equation by 5. 5(p + n = 240) 5 p + 8 n = 1614 Subtract the equations to eliminate p. 5 p + 5 n = 1200 5 p + 8 n = 1614 0 – 3 n = – 414

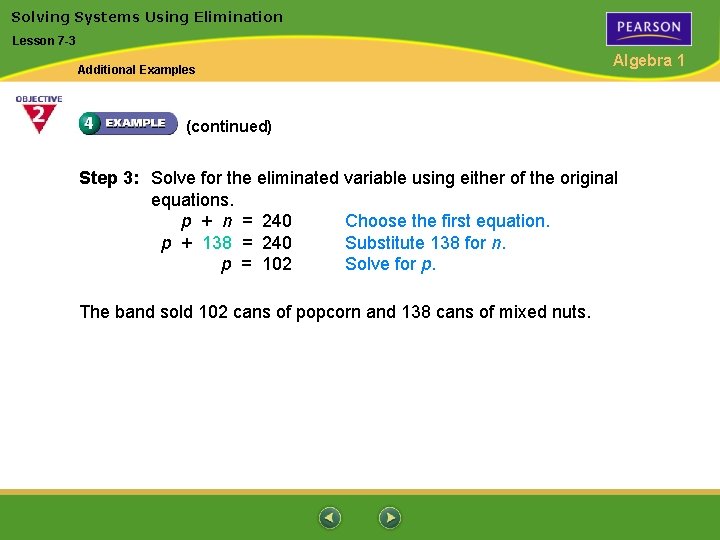
Solving Systems Using Elimination Lesson 7 -3 Additional Examples Algebra 1 (continued) Step 3: Solve for the eliminated variable using either of the original equations. p + n = 240 Choose the first equation. p + 138 = 240 Substitute 138 for n. p = 102 Solve for p. The band sold 102 cans of popcorn and 138 cans of mixed nuts.

Solving Systems Using Elimination Lesson 7 -3 Algebra 1 Additional Examples Solve by elimination. 5 x + 7 y = 10 3 x + 5 y = 10 Step 1: Eliminate one variable. Start with the given system. 3 x + 5 y = 10 5 x + 7 y = 10 Step 2: Solve for y. 4 y = 20 y = 5 To prepare to eliminate x, multiply one equation by 5 and the other equation by 3. 5(3 x + 5 y = 10) 3(5 x + 7 y = 10) Subtract the equations to eliminate x. 15 x + 25 y = 50 15 x + 21 y = 30 0 + 4 y = 20

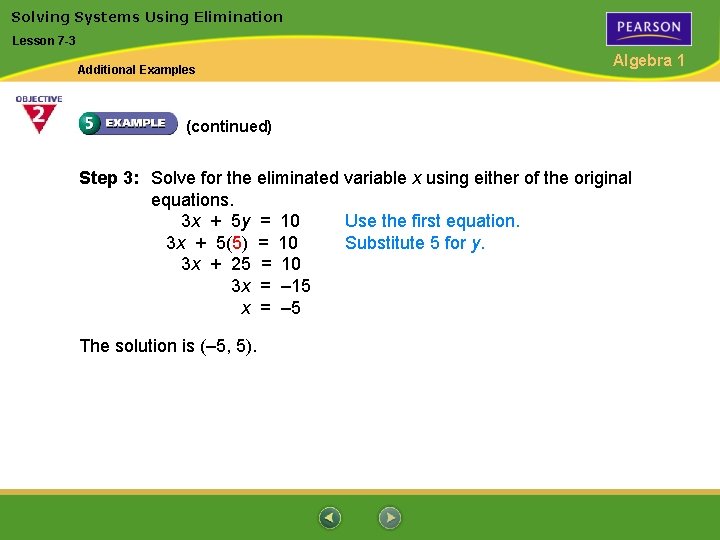
Solving Systems Using Elimination Lesson 7 -3 Additional Examples Algebra 1 (continued) Step 3: Solve for the eliminated variable x using either of the original equations. 3 x + 5 y = 10 Use the first equation. 3 x + 5(5) = 10 Substitute 5 for y. 3 x + 25 = 10 3 x = – 15 x = – 5 The solution is (– 5, 5).