Solving Systems of Linear equations with three Variables

Solving Systems of Linear equations with three Variables n r a e l l l ’ u o y t ha W To solve system s in three variables using elimination To solve system in three variables using substitution To real world problems involving systems of linear equations in three variables. A linear system in three variables determines a collection of planes. The intersection points are the solution.

Steps to solving a system of equations in three variables 1. Ensure that the equations are in standard form: Ax + By + Cz = D 2. Remove any decimals or fractions from the equations. 3. Eliminate one of the variables using two of the three equations. Result will be a new equation with two variables. 4. Eliminate the same variable using another set of two equations. Result will be a second equation in two variables. 5. Solve the new system of two equations. Using the solution for the two variables, substitute the values into one of the original equations to solve for the third variable. 6. Check the solution set in the remaining two original equations.

Solve 1 2 Ensure that all equations are in standard form 3 3 1 2 then 3 Eliminate the fractions and decimals. Easy to work. 2 1

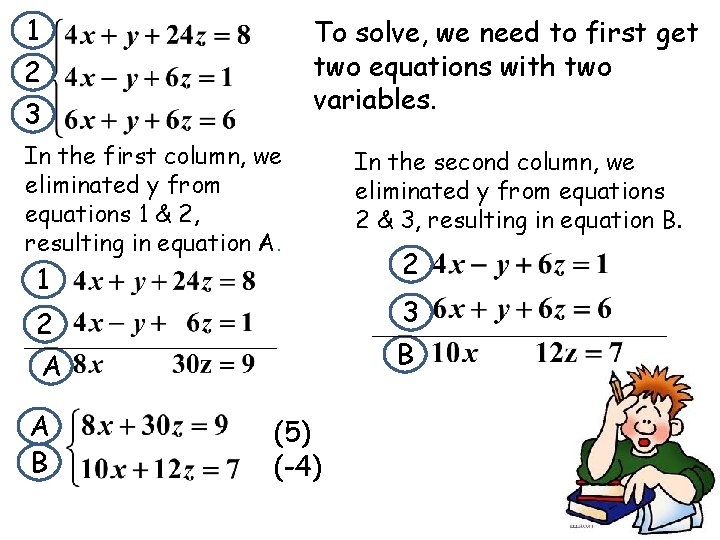
1 2 3 To solve, we need to first get two equations with two variables. In the first column, we eliminated y from equations 1 & 2, resulting in equation A. 1 2 3 B 2 A A B In the second column, we eliminated y from equations 2 & 3, resulting in equation B. (5) (-4)

Now substitute the value for of z into equation A or B to solve for x; We are using equation B: Next we need to substitute the values of x and z into one of the original equations to solve for y. We’ll use equation 2 (after decimals were removed): The solution for the system of equations is the ordered triple:

To check your answer Equation 1: Substitute the values for x, y, z Simplify The resulting statement is true. Equation 3: Substitute the values for x, y, z Simplify The resulting statement is true

Independent, Dependent and Inconsistent Equations Systems of three equations in three variables follow the same characteristics of systems of equations in two variables Independent equations have one solution Dependent equations have an infinite number of solutions Inconsistent equations have no solution Solving a system of equations in three variables involves a few more steps, but is essentially the same process as for systems of two equations in two variables.

Take a note Our example problem resulted in one unique solution all drop out when adding two of the equations together set. However, this may not always be the case. If the variables, a unique solution is not possible. See the following examples. -5 x + 6 y – 3 z = 17 5 x – 6 y + 3 z = -2 0 = 15 2 x + y – z = 6 -2 x – y + z = -6 0 = 0 In this example, the variables all cancel out, and the result is a false statement. This indicates that there is no solution, and we have an inconsistent set of equations. In this example, the variables all cancel out, and the result is a true statement. This indicates that the equations are dependent and we have an infinite number of solutions.

Problem 2: Solving a system by substitution What is the x-value in the solution of the system? 1 2 3 Choose equation 2 to solve for x 2

Solving by substitution 2 x=9 -5 y Substitute the expression for x into equations 1 and 3 and simplify 1 2 x+3 y-2 z=-1 2(9 -5 y)+3 y-2 z=-1 18 -10 y+3 y-2 z=-1 -7 y-2 z=-19 A 3 4 z-5 x=4 4 z-5(9 -5 y)=4 4 z-45+25 y=4 25 y+4 z=49 B

A B Substitute y into A Now use one of the original equations to solve for x x+5 y=9 x+5(1)=9 x+5=9 x=4 The solution is (4, 1, 6)

Your turn A theater has 490 seats. Seats sell for $25. 00 on the floor, $20. 00 in the mezzanine and $15 in the balcony. The number of seats on the floor equals the number of seats in the mezzanine and the balcony. Suppose theater takes in $10, 520 from each sold out event. How many seats does the mezzanine section hold? Answer: m=144 f + m + b = 490 25 f+20 m+15 b=10, 520 f= m + b

Classwork odd Homework even