Solving Systems of Linear Equations Iterative Methods Dongshin

Solving Systems of Linear Equations: Iterative Methods Dongshin Kim Joongheon Kim Jihoon Myung Computer Networks Research Lab. Dept. of Computer Science and Engineering Korea University Computer Networks Research Lab. Korea University

Contents § § § Introduction Basic Idea Jacobi Method Gauss-Seidel Method Successive Over Relaxation (SOR) Summary 2

Introduction (1/2) § If systems of linear equations are very large, the computational effort of direct methods is prohibitively expensive § Three common classical iterative techniques for linear systems – The Jacobi method – Gauss-Seidel method – Successive Over Relaxation (SOR) method § Matlab’s built-in functions 3

Introduction (2/2) § For systems that have coefficient matrices with the appropriate structure – especially large, sparse systems (many coefficients whose value is zero) – iterative techniques may be preferable 4

Basic Idea § Convert the system into the equivalent system § Generate a sequence of approximation , where 5

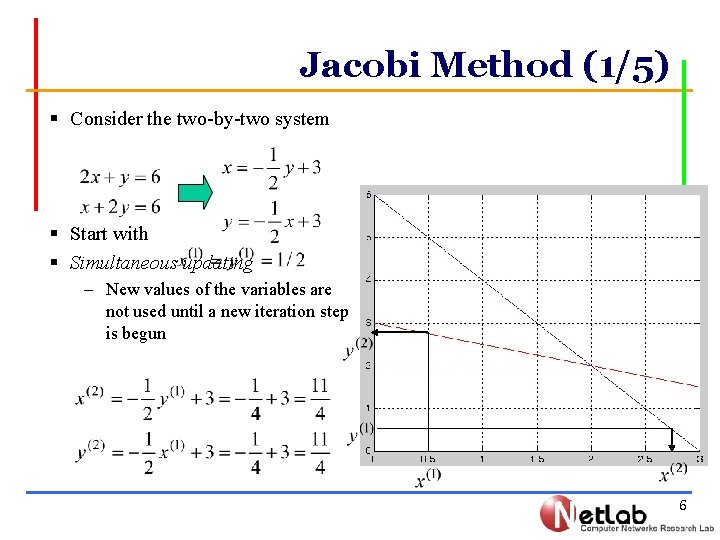
Jacobi Method (1/5) § Consider the two-by-two system § Start with § Simultaneous updating – New values of the variables are not used until a new iteration step is begun 6

Jacobi Method (2/5) § Con’t 7

Jacobi Method (3/5) § Consider the three-by-three system § Start with 8

Jacobi Method (4/5) § Matlab function for jacobi method 9

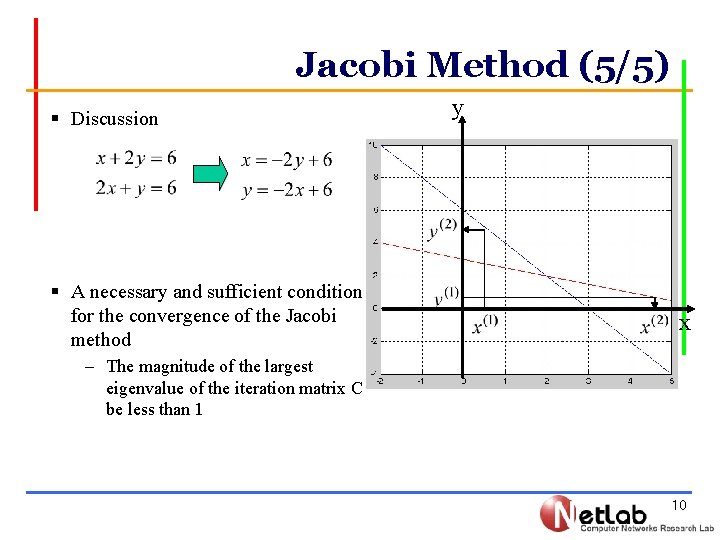
Jacobi Method (5/5) § Discussion § A necessary and sufficient condition for the convergence of the Jacobi method y x – The magnitude of the largest eigenvalue of the iteration matrix C be less than 1 10

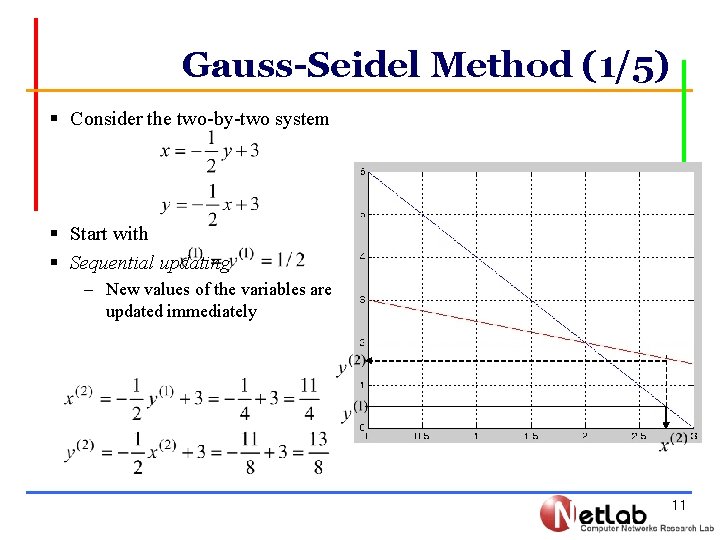
Gauss-Seidel Method (1/5) § Consider the two-by-two system § Start with § Sequential updating – New values of the variables are updated immediately 11

Gauss-Seidel Method (2/5) § Con’t 12

Gauss-Seidel Method (3/5) § Consider the three-by-three system § Start with 13

Gauss-Seidel Method (4/5) § Matlab function for gauss-seidel method 14

Gauss-Seidel Method (5/5) § Discussion – The Gauss-Seidel method is sensitive to the form of the co-efficient matrix A – The Gauss-Seidel method typically converges more rapidly than the Jacobi method – The Gauss-Seidel method is more difficult to use for parallel computation 15

Successive Over Relaxation (SOR) (1/5) § Introduce an additional parameter, ω, that may accelerate the convergence of the iterations 16

Successive Over Relaxation (SOR) (2/5) § Consider the three-by-three system 17

Successive Over Relaxation (SOR) (3/5) § Required number of iterations for different values of the relaxation parameter – Start with – Tolerance = 0. 00001 ω 0. 8 0. 9 1. 0 1. 25 1. 3 1. 4 No. of iterations 44 36 29 18 15 13 16 18

Successive Over Relaxation (SOR) (4/5) § Matlab function for SOR 19

Successive Over Relaxation (SOR) (5/5) § Discussion – The SOR method can be derived by multiplying the decomposed system obtained from the Gauss-Seidel method by the relaxation parameter w – The iterative parameter w should always be chosen such that 0<w<2 20

Summary § Jacobi method § Gauss-seidel method § SOR method 21