Solving systems of equations with 2 variables Word

Solving systems of equations with 2 variables Word problems (Coins)
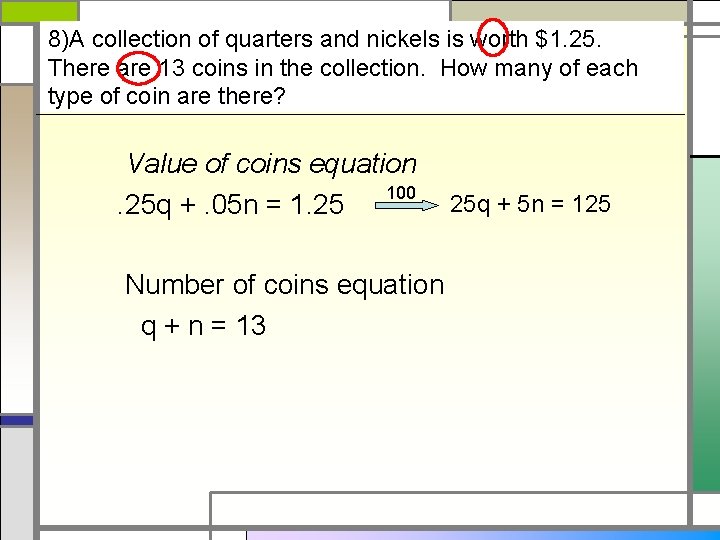
8)A collection of quarters and nickels is worth $1. 25. There are 13 coins in the collection. How many of each type of coin are there? Value of coins equation 100. 25 q +. 05 n = 1. 25 Number of coins equation q + n = 13 25 q + 5 n = 125

8)A collection of quarters and nickels is worth $1. 25. There are 13 coins in the collection. How many of each type of coin are there? 25 q + 5 n = 125 q + n = 13 Back substitution q + n = 13 3 + n = 13 n = 10 1 -5 25 q + 5 n = 125 -5 q – 5 n = -65 20 q = 60 q=3 There are 3 quarters and 10 nickels in the collection.

9)A collection of nickels and dimes is worth $25. There are 400 coins in the collection. How many of each type of coin are there? Value of coins equation 100. 05 n +. 10 d = 25 Number of coins equation q + n = 400 5 n + 10 d = 2500

9)A collection of nickels and dimes is worth $25. There are 400 coins in the collection. How many of each type of coin are there? 5 n + 10 d = 2500 n + d = 400 Back substitution n + d = 400 300 + d = 400 d = 100 1 -10 5 n + 10 d = 2500 -10 n – 10 d = -4000 -5 n = -1500 n = 300 There are 300 nickels and 100 dimes in the collection.

10)There are 429 people at a play. Admission is $1 for adults and 75 cents for children. The receipts were $372. 50. How many adults and children tickets were sold? Value of tickets equation 100 1 A +. 75 C = 372. 50 100 A + 75 C = 37250 Number of tickets equation A + C = 429

10)There are 429 people at a play. Admission is $1 for adults and 75 cents for children. The receipts were $372. 50. How many adults and children tickets were sold? 100 A + 75 C = 37250 A + C = 429 1 -75 Back substitution A + C = 429 203 + C = 429 C = 226 100 A + 75 C = 37250 -75 A – 75 C = -32175 25 A = 5075 A = 203 They sold 203 adult tickets and 226 children tickets.
- Slides: 7