Solving Systems of Equations Solving a System with


























- Slides: 33

Solving Systems of Equations

Solving a System with Several Equations in Several Unknowns Rule of Thumb: • More equations than unknowns system is unlikely to have a solution. • Same number of equations as unknowns system is likely to have a unique solution. • Fewer equations than unknowns the system is likely to have infinitely many solutions. We are interested in this last situation!

Solving a System with Several Equations in Several Unknowns Rule of Thumb: • More equations than unknowns system is unlikely to have a solution. • Same number of equations as unknowns system is likely to have a unique solution. • Fewer equations than unknowns the system is likely to have infinitely many solutions. We expect to have as many “free variables” as the difference between the number of unknowns and the number of equations.

Systems of Equations Linear system. Matrix methods. Non-linear system. Can be solved analytically More difficult!

Linear Systems of Equations We can write this as a matrix/vector equation as follows: We can solve this system using “elementary row operations”

Row Reduce the Matrix

Solving the System Now we can reinterpret this reduced matrix as a solution to the system of equations.

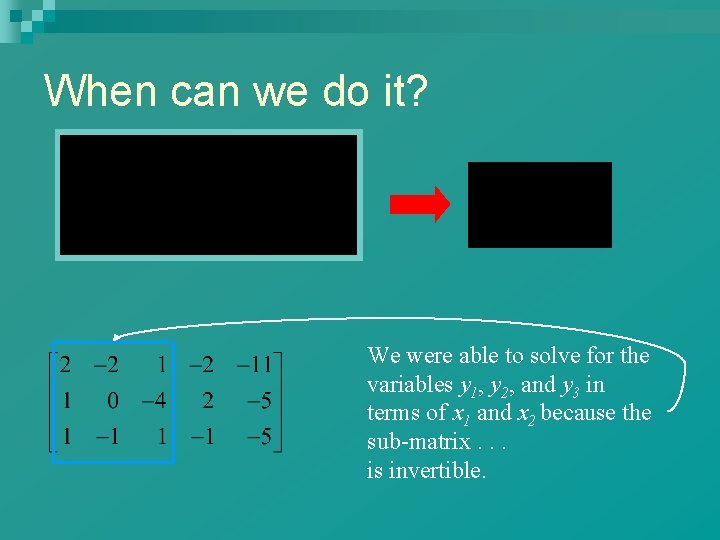
When can we do it? We were able to solve for the variables y 1, y 2, and y 3 in terms of x 1 and x 2 because the sub-matrix. . . is invertible.

The Solution Function We started with three equations in five unknowns. As expected, our first three unknowns depend on two “free variables, ” two being the difference between the number of unknowns and the number of equations.


Non-linear Equations Though we completely understand how to solve systems of linear equations. . . and we “luck out” with a small number of non-linear systems. . . most are impossible to solve analytically!

So How do we Proceed? This equation is already too hard…. We’ll start with something a bit simpler. What would you do with this one?

So How do we Proceed? This equation is already too hard…. We’ll start with something a bit simpler. What would you do with this one?

Iterating real functions M: → is a continuous function. Suppose that we iterate M beginning with x=x 0 to obtain the sequence Fact: If the iterated map converges, then it converges to a fixed point of M. That is, it converges to a real number x such that M(x) = x. This sequence is called the iterated map on M based at x 0.

Why a Fixed Point? Together with the continuity of M these should tell us that: But this is just the “tail” of the sequence that converged to x! Removing the first term won’t affect convergence, so M (x) = x

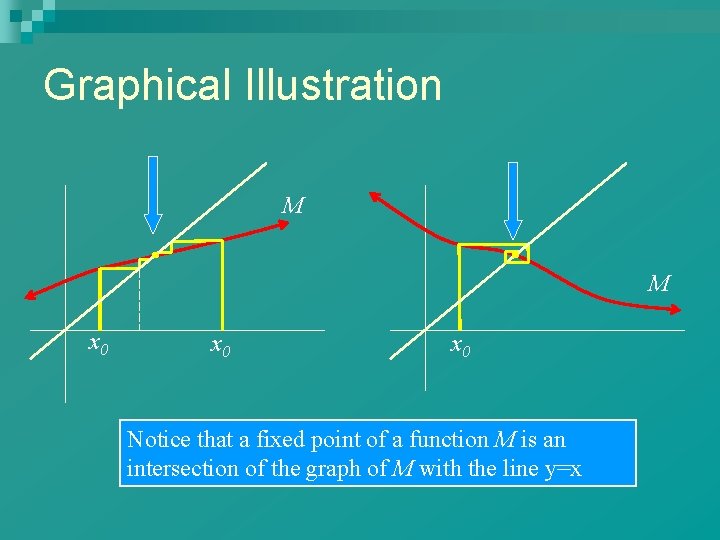
Graphical Illustration M M x 0 x 0 Notice that a fixed point of a function M is an intersection of the graph of M with the line y=x

Solving equations Suppose we want to find a root for the equation We can rewrite the equation as and reinterpret the problem as a fixed point problem.

Root finding via iteration When we iterate the function starting at x 0=0, we get The limit is, indeed, a solution to the equation

Problem. . . This works nicely when the iterated map converges, but it may not converge. For instance, if we try the same trick with the iterated map goes to infinity. What’s the difference? What’s going on?

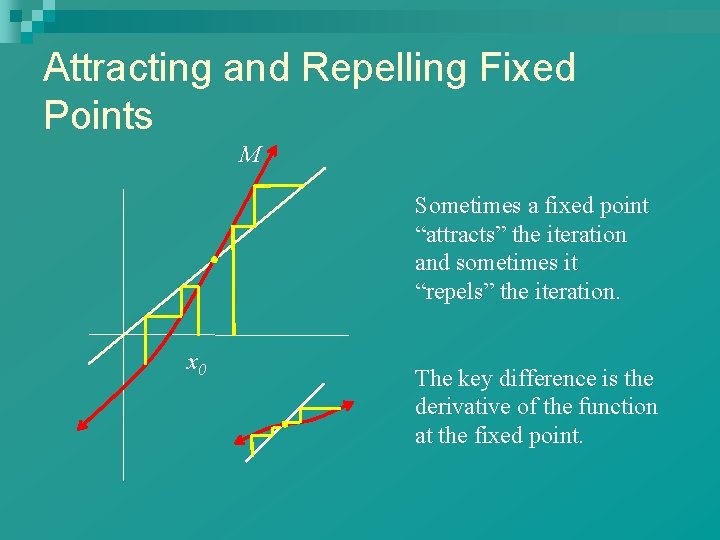
Attracting and Repelling Fixed Points M Sometimes a fixed point “attracts” the iteration and sometimes it “repels” the iteration. x 0 The key difference is the derivative of the function at the fixed point.

The Derivative at the Fixed Point Theorem: Suppose that M is continuously differentiable on [a, b] and that p is a fixed point of M lying in [a, b]. If then there exists some subinterval I of [a, b] containing p such that if x 0 is in I, then Conversely, if then there is some interval I about p such that every iterated map based a point of I (other than p, of course) will eventually leave I and will thus not converge to p.

Rethinking the scheme Let x be a real number and K a non-zero real number. Note that x is a solution to the equation if and only if it is also a solution to the equation So our fixed point root-finding scheme can be applied to any equation of the form Choose the value of K so that the derivative is “favorable”

The best of all possible worlds It is not hard to show that the rate at which the iterated maps on M converge to the fixed point p is governed by the size of | M '(p) |. The closer | M '(p) | is to zero, the faster the convergence rate. While we are making choices, we might as well be ambitious and choose K so that we not only get convergence to the root, but we get really fast convergence! For we want Works, provided that f '(p) 0.

So in the best of all possible worlds, we want to iterate the function where p is a root of f. Constant (given p!), and ideally chosen for convergence near p. Notice that this looks remarkably like the iteration function for Newton’s method: Evaluated each step, but not far from f’(p) when x is close to p.

Quasi-Newton methods: Iterative ways to find p with f (p) = 0 Newton’s method Must evaluate new f’(x) each step. Requires no “magic knowledge” and converges in a neighborhood of p. “Leibnitz” method “Best of all possible worlds”: Since M’(p) = 0, iterated maps converge very quickly in a neighborhood of p. “Pretty good” method If we choose D near enough to f’(p) so that |Q’(p)| < 1/2, iterated maps will converge in a neighborhood of p.

One Equation in Two Unknowns Can we use this set of ideas to tackle Yes! First we recall that the solutions to this equation are the zeros of the 2 -variable function

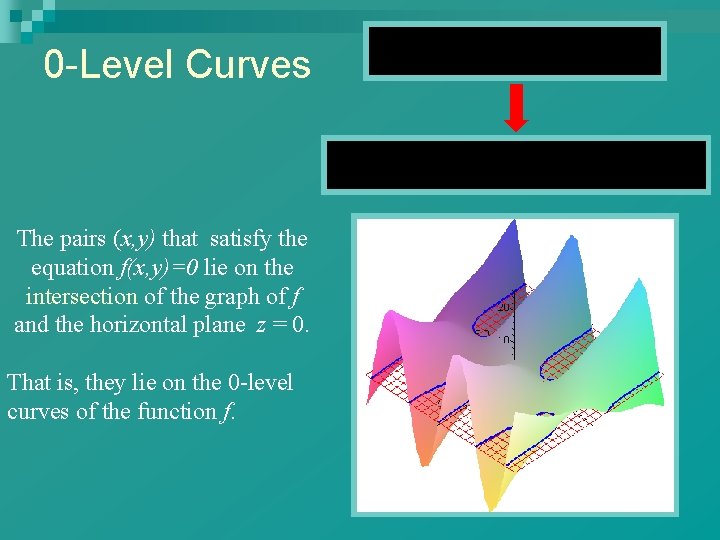
0 -Level Curves The pairs (x, y) that satisfy the equation f(x, y)=0 lie on the intersection of the graph of f and the horizontal plane z = 0. That is, they lie on the 0 -level curves of the function f.

Taking a “piece” The 0 -level curves of f. Though the points on the 0 -level curves of f do not form a function, portions of them do.

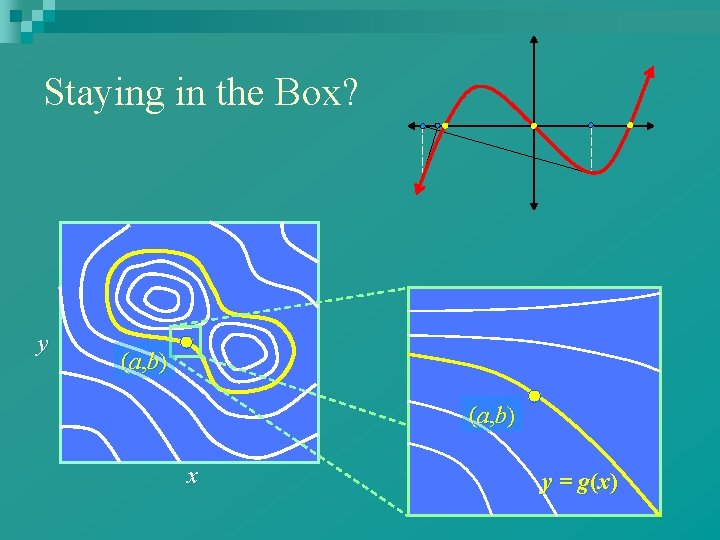
y x Consider the contour line f (x, y) = 0 in the xy-plane. Idea: At least in small regions, this curve might be described by a function y = g(x). Our goal: find such a function!

In a small box around (a, b), we can hope to find g(x). y Make sure all of the y-partials in this box are close to D. (a, b) x Start with a point (a, b) on the contour line, where the partial with respect to y is not 0: (a, b) y = g(x)

How to construct g(x): For this x, construct function (a, b) Iterate x(y) to find its fixed point, where f (x, y) = 0. Let fixed point be g(x). Fix xx. z f (x, y) (x fixed) What’s going on here? For our fixed value of x, we find g(x) so that f (x, g(x)) = 0. We are doing this by iteration. g(x) y

How to construct g(x) Given x, construct function (a, b) Iterate x(y) to find its fixed point, where f (x, y) = 0. Let fixed point be g(x). x b How do we know this works? For x = a, this is just the ideal “Leibnitz” method for finding g(a) = b. For small enough boxes, this is a “pretty good” method elsewhere. Non-trivial issues: • Make sure the iterated map converges • Make sure you get the right fixed point. (Don’t leave the box!)

Staying in the Box? y (a, b) x y = g(x)