Solving Systems of Equations by Adding What is

Solving Systems of Equations by Adding

What is a System? A system refers to two lines graphed on the same coordinate plane. The solution to a system is the point or points that the two lines have in common.
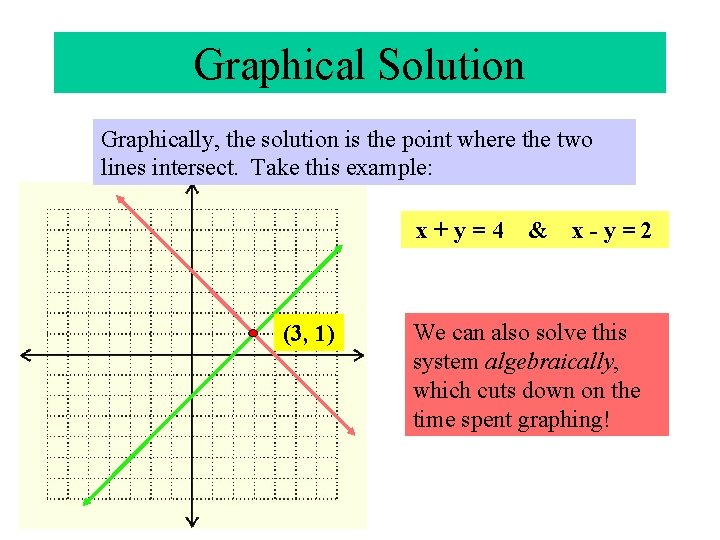
Graphical Solution Graphically, the solution is the point where the two lines intersect. Take this example: x+y=4 (3, 1) & x-y=2 We can also solve this system algebraically, which cuts down on the time spent graphing!
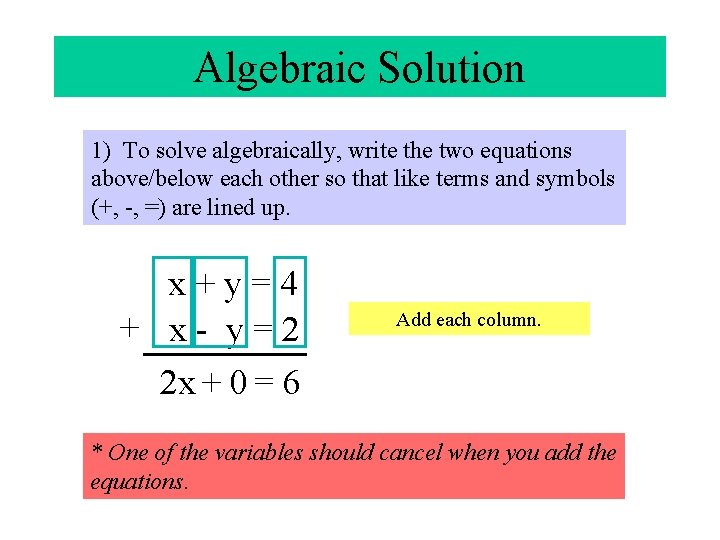
Algebraic Solution 1) To solve algebraically, write the two equations above/below each other so that like terms and symbols (+, -, =) are lined up. x+y=4 + x- y=2 2 x + 0 = 6 Add each column. * One of the variables should cancel when you add the equations.

Algebraic Solution 2) Solve the equation that is left. x+y=4 + x- y=2 2 x + 0 = 6 2 x = 6 1 • 2 x = 2 6 2 x=3 Solve.

Algebraic Solution 3) Substitute the solution for x into either of the system equations and solve for y. Substitute x = 3. x+y=4 3 + y + (-3) = 4 + (-3) The solution is: (3, 1) 0+y=1

Example #2 x + 3 y = 4 + -x - 2 y = 2 + Change the subtraction in the 2 nd equation to addition (Keep-Change. ). x + 3 y = 4 (-x) + (-2 y) = 2 0 + 1 y = 6 Add the columns. * One of the variables should cancel when you add the equations.

Example #2 0 + 1 y = 6 y=6 Solve. Substitute y = 6 into either equation and solve for x. x + 3 y = 4 x + 3(6) = 4 x + 18 + (-18) = 4 + (-18) x = -14 The solution is (-14, 6)

Example #3 2 x + 3 y = 6 + x - 3 y = 3 + Change the subtraction in the 2 nd equation to addition (Keep-Change. ). 2 x + 3 y = 6 x + (-3 y) = 3 3 x + 0 = 9 Add the columns. * One of the variables should cancel when you add the equations.

Example #3 Solve. 3 x + 0 = 9 1 • 3 x = 1 • 9 3 3 x=3

Example #3 Substitute x = 3 into either equation and solve for x. x + (-3 y) = 3 3 + (-3 y) + (-3) = 3 + (-3) (-3 y) = 0 1 • (-3 y) = 1 • 0 -3 -3 y=0 The solution is (3, 0).
- Slides: 11