Solving systems Elimination Method Lesson 2 9 y




















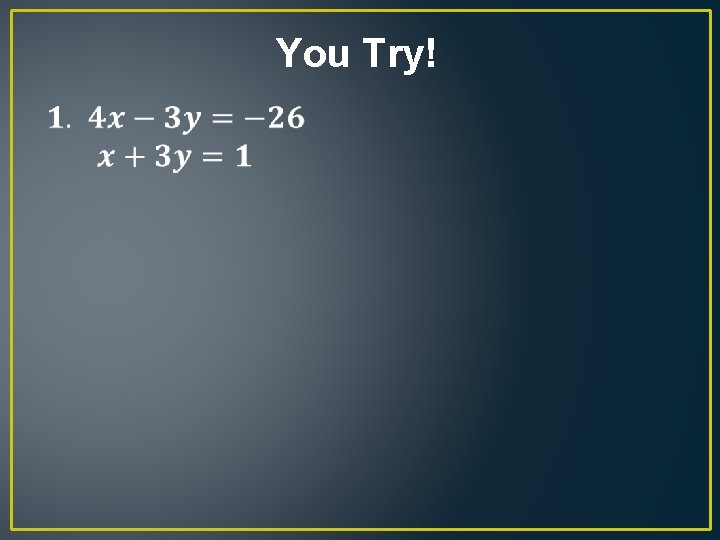


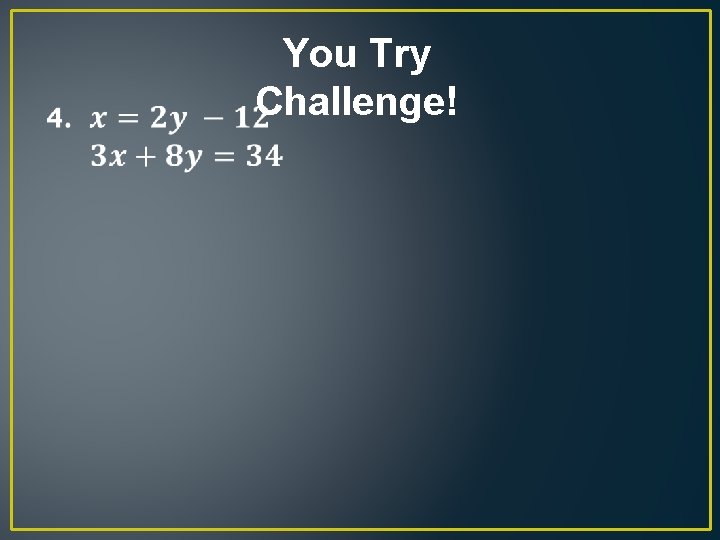

- Slides: 25

Solving systems…. . Elimination Method! Lesson 2. 9 (y do I have to get rid of x? ) ‘In Common’ Ballad: http: //youtu. be/Br 7 qn 4 y. Lf-I ‘All I do is solve’ Rap: http: //youtu. be/1 q. HTmxla. ZWQ

Concept: Solving Systems of Equations Essential Question: How can I manipulate equation(s) to solve a system of equations? (standards REI 5 -6, 10 -11) Vocabulary: Elimination/Algebraically/Linear Combination Method

Example 1 Solve the following system by elimination.

1. Write your equations so that the corresponding variables are aligned. Notice 2 x is above x and -3 y is above 3 y

2. Check to see if the same variable has the same coefficient. The coefficients y differ only by a sign. 3. Multiply to make the coefficients the same value, but different signs. Our example has 3 y and -3 y so we can move on to step 4.

4. Use addition to eliminate one of the variables. 5. Solve for the variable. 3 x = 0 x=0

6. Continue solving the system to find the remaining variable. Using an original equation, substitute the value you found for y.

7. Write the solution as a point.

Example 2: 1. Write your equations so that the corresponding variables are aligned. x + 4 y = 0 3 x + 2 y = 20 Notice x is above 3 x and 4 y is above 2 y

2. Check to see if the same variable has the same coefficient. Example 2: x + 4 y = 0 3 x + 2 y = 20 The coefficients are different for x and y.

3. Multiply to make the coefficients the same value, but different signs. x + 4 y = 0 3 x + 2 y = 20 -3(x + 4 y = 0) 3 x + 2 y = 20 - 3 x - 12 y = 0 3 x + 2 y = 20 How can we make the coefficients of x the same but with different signs?

4. Use addition to eliminate one of the variables. - 3 x - 12 y = 0 + 3 x + 2 y = 20 -10 y = 20 5. Solve for the variable. -10 y = 20 y = -2

6. Continue solving the system to find the remaining variable. Using an original equation, substitute the value you found for y. x + 4 y = 0 x + 4(-2) = 0 x– 8=0 x=8

7. Write the solution as a point. Solution: (8, -2)

Example 3: 1. Write your equations so that the corresponding variables are aligned. 2 x + 3 y = 9 3 x + 4 y = 15 Notice 2 x is above 3 x and 3 y is above 4 y

2. Check to see if the same variable has the same coefficient. Example 3: 2 x + 3 y = 9 3 x + 4 y = 15 The coefficients for x and y are not the same.

3. Use multiplication or division to make one of the variables have the same How can we make coefficient but different signs. 2 x + 3 y = 9 3 x + 4 y = 15 3(2 x + 3 y = 9) -2(3 x + 4 y = 15) 6 x + 9 y = 27 -6 x – 8 y = -30 the coefficients of x the same but with different signs?

4. Use addition to eliminate one of the variables. 6 x + 9 y = 27 -6 x – 8 y = -30 y = -3 5. Solve for the variable (we can skip this step because the variable is already solved). y = -3

6. Continue solving the system to find the remaining variable. Using an original equation, substitute the value you found for y. 2 x + 3 y = 9 2 x + 3(-3) = 9 2 x – 9 = 9 2 x = 18 x=9

7. Write the solution as a point. Solution: (9, 3)
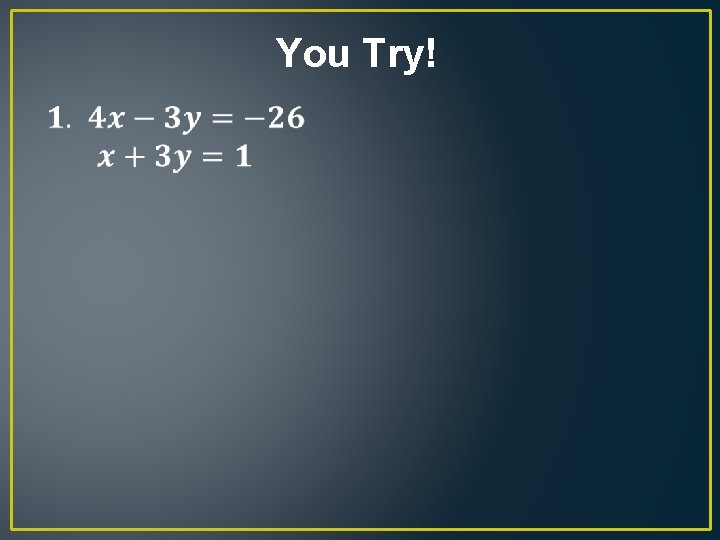
You Try!

You Try!

You Try!
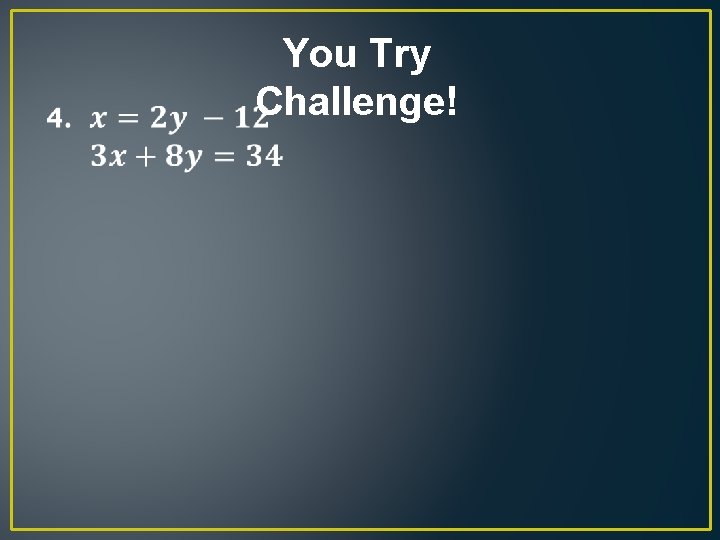
You Try Challenge!

$2. 00 Summary…. Each word is worth 10 cents. Write a summary describing how to solve a system using the elimination method.