Solving Systems by Graphing Section 6 1 Goals

Solving Systems by Graphing Section 6 -1

Goals Goal Rubric • To solve systems of equations by graphing. • To analyze special systems. Level 1 – Know the goals. Level 2 – Fully understand the goals. Level 3 – Use the goals to solve simple problems. Level 4 – Use the goals to solve more advanced problems. Level 5 – Adapts and applies the goals to different and more complex problems.

Vocabulary • System of Linear Equations • Solutions of a System of Linear Equations

Definition • System of Linear Equations - a set of two or more linear equations containing two or more variables. – Example: • Solution of a System of Linear Equations – is an ordered pair that satisfies each equation in the system. So, if an ordered pair is a solution, it will make both equations true.

Solutions A system of linear equations is a grouping of two or more linear equations where each equation contains one or more variables. y = – 4 x – 6 5 x + 3 y = – 8 y = 2 x x – 4 y = 7 A brace is used to remind us that we are dealing with a system of equations. A solution of a system of equations consists of values for the variables that satisfy each equation of the system. When we are solving a system of two linear equations containing two unknowns, we represent the solution as an ordered pair (x, y), a point.

Example: Identifying Solutions to a System Tell whether the ordered pair is a solution of the given system. (5, 2); 3 x – y = 13

Example: Identifying Solutions to a System Tell whether the ordered pair is a solution of the given system. (– 2, 2); x + 3 y = 4 –x + y = 2

Your Turn: Tell whether the ordered pair is a solution of the given system. (1, 3); 2 x + y = 5 – 2 x + y = 1

Your Turn: Tell whether the ordered pair is a solution of the given system. x – 2 y = 4 (2, – 1); 3 x + y = 6

Example: Writing a System of Equations Wren and Jenni are reading the same book. Wren is on page 14 and reads 2 pages every night. Jenni is on page 6 and reads 3 pages every night. After how many nights will they have read the same number of pages? How many pages will that be?

Your Turn: Video club A charges $10 for membership and $3 per movie rental. Video club B charges $15 for membership and $2 per movie rental. For how many movie rentals will the cost be the same at both video clubs? What is that cost?

System Solution on a Graph All solutions of a linear equation are on its graph. To find a solution of a system of linear equations, you need a point that each line has in common. In other words, you need their point of intersection. y = 2 x – 1 y = –x + 5 The point (2, 3) is where the two lines intersect and is a solution of both equations, so (2, 3) is the solution of the systems.

Solving a System by Graphing Steps for Obtaining the Solution of a System of Linear Equations by Graphing Step 1: Graph the first equation in the system. Step 2: Graph the second equation in the system. Step 3: Determine the point of intersection, if any. Step 4: Verify that the point of intersection determined in Step 3 is a solution of the system. Remember to check the point in both equations.

Example: System solution by Graphing Solve the system by graphing. Check your answer. y=x y = – 2 x – 3 The solution appears to be at (– 1, – 1). Graph the system.

Additional Example 2 B: Solving a System Equations by Graphing Solve the system by graphing. Check your answer. y=x– 6 y+ x = – 1

Check It Out! Example 2 a Solve the system by graphing. Check your answer. y = – 2 x – 1 y=x+5

Check It Out! Example 2 b Solve the system by graphing. Check your answer. 2 x + y = 4

Check It Out! Example 2 b Continued Solve the system by graphing. Check your answer. 2 x + y = 4

System Possible Solutions • There are three possible outcomes or solutions when graphing two linear equations in a plane. • One point of intersection, so one solution. • Parallel lines, so no solution. • Same lines, so infinite # of solutions.

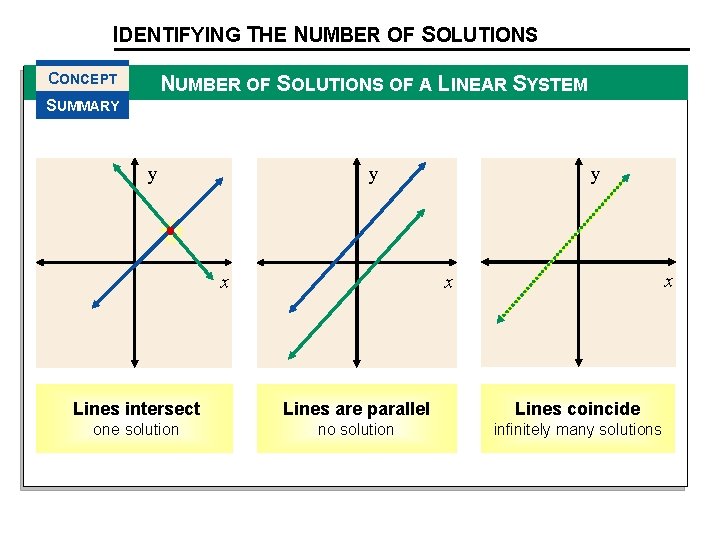
IDENTIFYING THE NUMBER OF SOLUTIONS CONCEPT NUMBER OF SOLUTIONS OF A LINEAR SYSTEM SUMMARY y y y x x x Lines intersect Lines are parallel Lines coincide one solution no solution infinitely many solutions