Solving simultaneous linear equations on the problems of

Solving simultaneous linear equations on the problems of linear relative motion Speed Formula: Distance = Speed × Time

e. g. 1 ) Two cars A and B are at a certain distance apart. The speed of car A is 72 km/h while the speed of car B is 48 km/h. If they start at the same time and they travel towards each other, they will meet in two hours. Find the distance between them. They meet in two hours 72 x 2 = 144 km A 48 x 2 = 96 km B The distance between them : 144 km + 96 km = 240 km

e. g. 2) May and Bobby are at a certain distance apart. The walking speed of May is 3 km/h and that of Bobby is 7 km/h. If they walk in the same direction, Bobby will catch up with May in 5 hours. a ) Find the distance between them. 7 x 5 = 35 km 3 x 5 = 15 km Bobby May The distance between them : 35 km - 15 km = 20 km b) How about if Bobby overtakes May in 3 hours ? The distance between them : 7 x 3 – 3 x 3 = 21 – 9 = 12 km

Learn how to set up equations to solve the problems

e. g. 3 ) A and B are 42 km apart. If they walk towards each other, they will meet after 3 hours. Set up an equation with two unknown speeds. Let x be A’s speed and y be B’s speed km/h They meet after 3 hours : x km : y km A 42 km B After 1 hour, how far will A walk ? After 3 hours, how far will A walk ? After 1 hour, how far will B walk ? After 3 hours, how far will B walk ? How to equate the distances ? x km 3 x km y km 3 x + 3 y = 42

e. g. 4) A and B are 22 km apart. If they walk in the same direction, A will catch up with B after 9 hours. Set up an equation with two unknown speeds. Let x km/h be A’s speed and y km/h be B’s speed : x km A will catch up with B after 9 hours 9 x km : y km 9 y km A B 22 km How far will A walk after 1 hour ? x km How far will A walk after 9 hours ? 9 x km How far will B walk after 1 hour ? y km How far will B walk after 9 hours ? 9 y km How to equate the distances ? 9 x – 9 y = 22 or 9 x = 22 + 9 y Do worksheet : No. 1 -4

1) David and Mary are 16 km apart. If they walk towards each other, they will meet in 2 hours. Let x km/h be the speed of David and y km/h be the speed of Mary. Set up an equation with x and y. : x km They meet after 2 hours : y km David 16 km Mary 2 x + 2 y = 16

2) A man and a boy are 18 km apart. If they run in the same direction, the man will catch up with the boy in 4 hours. Let x km/h be the speed of the man and y km/h be the speed of the boy. Set up an equation with x and y. : x km : y km 4 x km 4 y km Man 18 km Boy 4 x – 4 y = 18 or 4 x = 18 + 4 y

3) Two trains M and N are 250 km apart. If they start at the same time and they travel towards each other, they will meet after 50 minutes. Set up an equation with two unknown speeds. Let x km/min be the speed of train M and y km/min be the speed of train N. 50 x km After 50 minutes 50 y km Let x km/h be the speed of train M and y km/h be the Train M Train N 250 km speed of train N. 50 x + 50 y = 250

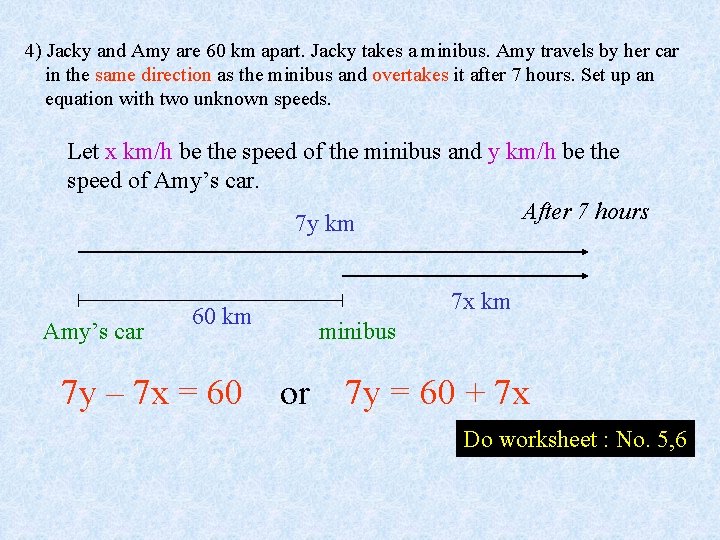
4) Jacky and Amy are 60 km apart. Jacky takes a minibus. Amy travels by her car in the same direction as the minibus and overtakes it after 7 hours. Set up an equation with two unknown speeds. Let x km/h be the speed of the minibus and y km/h be the speed of Amy’s car. After 7 hours 7 y km Amy’s car 60 km 7 x km minibus 7 y – 7 x = 60 or 7 y = 60 + 7 x Do worksheet : No. 5, 6

5) Tommy and Martin ride bicycles on the same road at constant speeds and they are a certain distance apart. The speed of Martin’s bicycle is 15 km/h. If they travel in the same direction, Tommy’s bicycle will catch up with Martin’s bicycle in 8 hours. a) Draw a diagram to show the situation. b) Set up an equation with the unknown distance apart and the unknown speed of Tommy’s bicycle. Let x km be the distance apart and y km/h be the speed of Tommy’s bicycle. After 8 hours 8 y km = 120 km Tommy’s bicycle x km Martin’s bicycle 8 y – 120 = x or 8 y = x + 120

6) A car and a bicycle are 72 km apart. The speed of the bicycle is 12 km/h. If they travel towards each other, they will meet after some time. a) Draw a diagram to show the situation. b) Set up an equation with the unknown time and the unknown speed of the car. Let x hours be the time and y km/h be the speed of the car. They meet after x hours 12 x km xy km car 72 km xy + 12 x = 72 bicycle

e. g. 5) Two cars P and Q are 480 km apart. If they start at the same time and travel towards each other, they will meet in three hours. If they travel in the same direction, car Q will overtake car P in eight hours. Find the speeds of cars P and Q. Let x km/h be the speed of car P and y km/h be the speed of car Q. 3 x km 3 x + 3 y = 480 P 3 y km 480 km Q 8 y km 8 x km P 8 y – 8 x = 480 or 8 y = 8 x + 480

Solve the simultaneous linear equations: …(1) …(2) Do worksheet : No. 7 Substitute into (1), The speed of car P is 50 km/h and the speed of car Q is 110 km/h.

7) Teddy and Ann are a certain distance apart. They ride bicycles at uniform speeds. The speed of Teddy’s bicycle is 18 km/h. If they ride towards each other, they will meet in 2 hours. If they ride in the same direction, Teddy will overtake Ann in 10 hours. Find the speed of Ann’s bicycle and the original distance apart. ( Set up two simultaneous linear equations. ) Let x km/h be the speed of Ann’s bicycle and y km be the original distance apart. 36 km Teddy’s bicycle y km 2 x km Ann’s bicycle 180 km Teddy’s bicycle y km 36 + 2 x = y 180 – 10 x = y 10 x km Ann’s bicycle

Solve the simultaneous linear equations: …(1) …(2) Substitute (1) into (2), Substitute x = 12 into (1), y + 10 x = 180 36 + 2 x = y 36 + 2 x + 10 x = 180 36 + 24 = y 12 x = 180 – 36 y = 60 12 x = 144 x = 12 The speed of Ann’s bicycle is 12 km/h and the original distance is 60 km.

Solving simultaneous linear equations on the problems of circular relative motion

e. g. 6) Cat A and cat B are running around a 640 m circular park. Cat A runs faster. If they start together ( at the same time and position ) and they go in opposite directions, they will meet in 35 seconds later. Let x m/s be cat A’s speed and y m/s be cat B’s speed. A B 35 y m 35 x + 35 y = 640 20 seconds later Do worksheet : No. 8

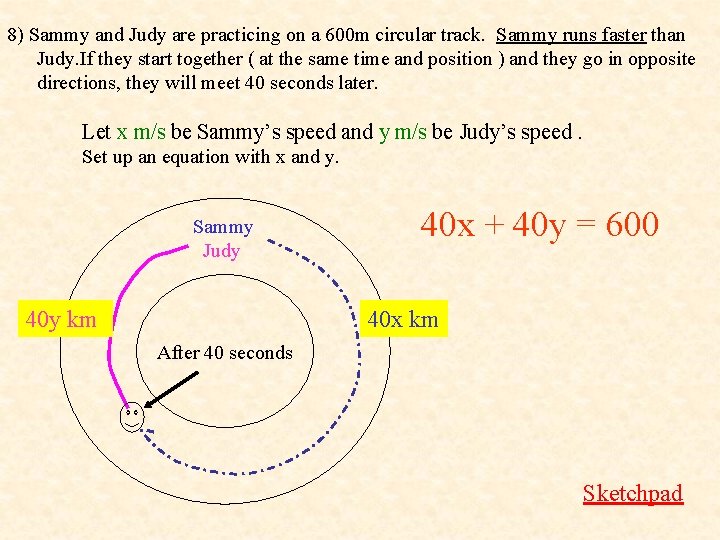
8) Sammy and Judy are practicing on a 600 m circular track. Sammy runs faster than Judy. If they start together ( at the same time and position ) and they go in opposite directions, they will meet 40 seconds later. Let x m/s be Sammy’s speed and y m/s be Judy’s speed. Set up an equation with x and y. Sammy Judy 40 y km 40 x + 40 y = 600 40 x km After 40 seconds Sketchpad

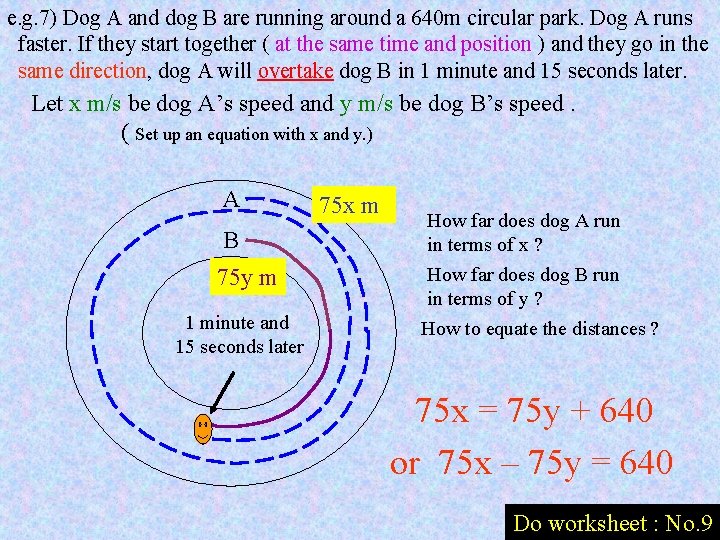
e. g. 7) Dog A and dog B are running around a 640 m circular park. Dog A runs faster. If they start together ( at the same time and position ) and they go in the same direction, dog A will overtake dog B in 1 minute and 15 seconds later. Let x m/s be dog A’s speed and y m/s be dog B’s speed. ( Set up an equation with x and y. ) A B 75 y m 1 minute and 15 seconds later 75 x m How far does dog A run in terms of x ? How far does dog B run in terms of y ? How to equate the distances ? 75 x = 75 y + 640 or 75 x – 75 y = 640 Do worksheet : No. 9

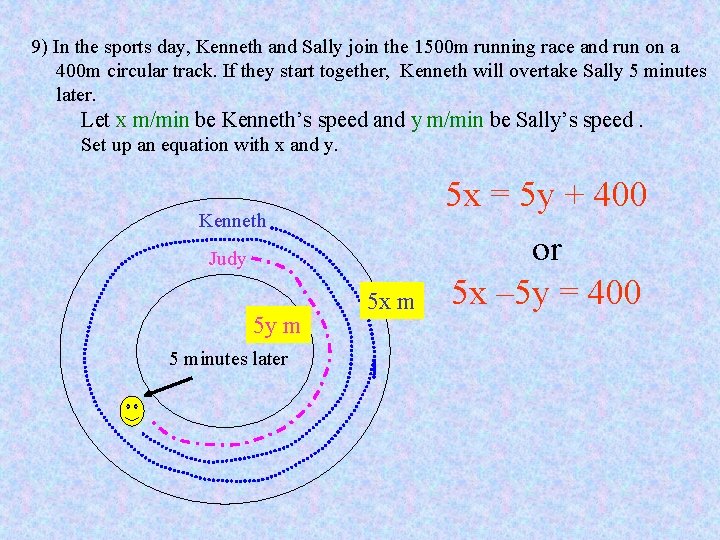
9) In the sports day, Kenneth and Sally join the 1500 m running race and run on a 400 m circular track. If they start together, Kenneth will overtake Sally 5 minutes later. Let x m/min be Kenneth’s speed and y m/min be Sally’s speed. Set up an equation with x and y. Kenneth Judy 5 y m 5 minutes later 5 x m 5 x = 5 y + 400 or 5 x – 5 y = 400

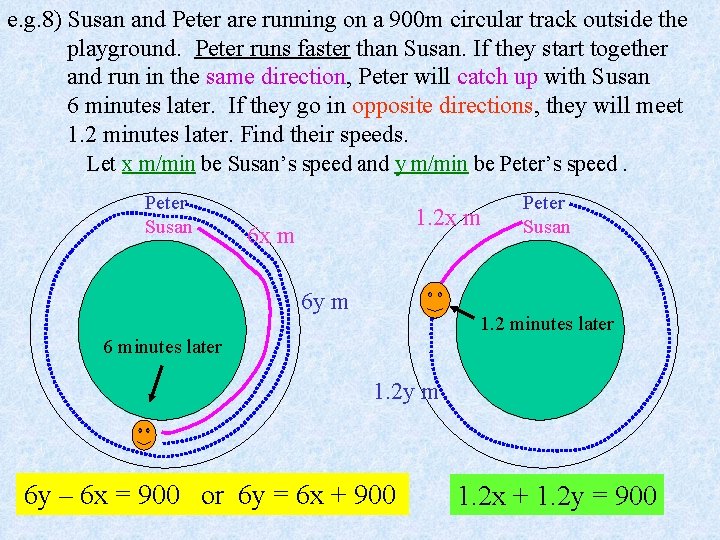
e. g. 8) Susan and Peter are running on a 900 m circular track outside the playground. Peter runs faster than Susan. If they start together and run in the same direction, Peter will catch up with Susan 6 minutes later. If they go in opposite directions, they will meet 1. 2 minutes later. Find their speeds. Let x m/min be Susan’s speed and y m/min be Peter’s speed. Peter 1. 2 x m Susan 6 x m 6 y m 1. 2 minutes later 6 minutes later 1. 2 y m 6 y – 6 x = 900 or 6 y = 6 x + 900 1. 2 x + 1. 2 y = 900

… (1) … (2) Do worksheet : No. 10 Substitute into (2), Susan’s speed is 300 m/min and Peter’s speed is 450 m/min.

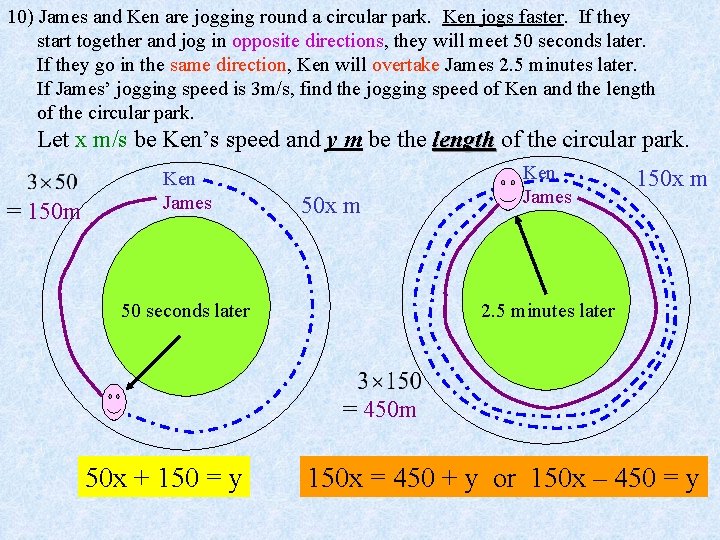
10) James and Ken are jogging round a circular park. Ken jogs faster. If they start together and jog in opposite directions, they will meet 50 seconds later. If they go in the same direction, Ken will overtake James 2. 5 minutes later. If James’ jogging speed is 3 m/s, find the jogging speed of Ken and the length of the circular park. Let x m/s be Ken’s speed and y m be the length of the circular park. length = 150 m Ken James 50 x m 50 seconds later Ken James 150 x m 2. 5 minutes later = 450 m 50 x + 150 = y 150 x = 450 + y or 150 x – 450 = y

…(1) …(2) Substitute (1) into (2), Substitute into (1), Ken’s speed is 6 m/s and the length of the circular park is 450 m.