Solving Quadratic Equations Using the Quadratic Formula Math

Solving Quadratic Equations Using the Quadratic Formula Math 2 Spring 2016 Mrs. Brown

Quadratic Formula Use this formula when factoring is not possible to solve a quadratic equation.

Example 1: Solve the equation using the Quadratic Formula

Example 2: Solve the equation

Example 3: Solve the equation

Stations Activity 1) You will have 3 minutes to solve the problem at your current station 2) After three minutes you will rotate to the next station. If you are at Station 8, you will rotate to Station 1 3) You must show your work. 4) Every person is responsible for their own work. You are traveling as a group but should do individual work. 5) I will collect these at the end of the activity for a grade.

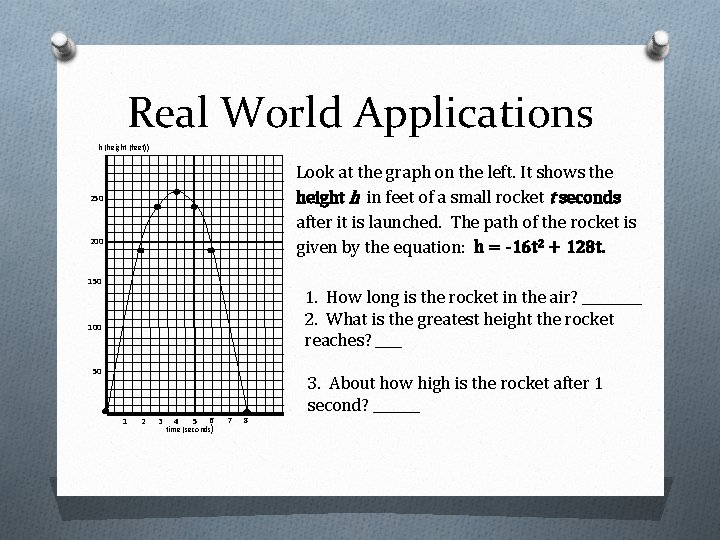
Real World Applications h (height (feet)) Look at the graph on the left. It shows the height h in feet of a small rocket t seconds after it is launched. The path of the rocket is given by the equation: h = -16 t 2 + 128 t. 250 200 150 1. How long is the rocket in the air? _____ 2. What is the greatest height the rocket reaches? ____ 100 50 3. About how high is the rocket after 1 second? _______ 1 2 3 4 5 6 time (seconds) 7 8

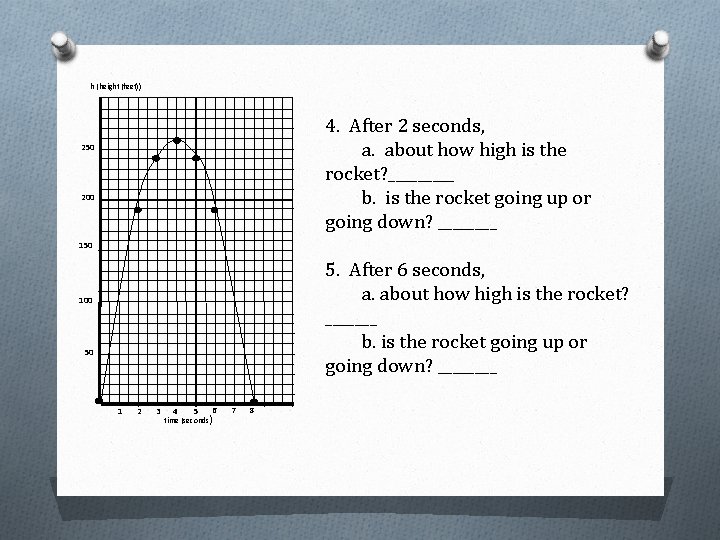
h (height (feet)) 4. After 2 seconds, a. about how high is the rocket? _____ b. is the rocket going up or going down? ____ 250 200 150 5. After 6 seconds, a. about how high is the rocket? _______ b. is the rocket going up or going down? ____ 100 50 1 2 3 4 5 6 time (seconds) 7 8

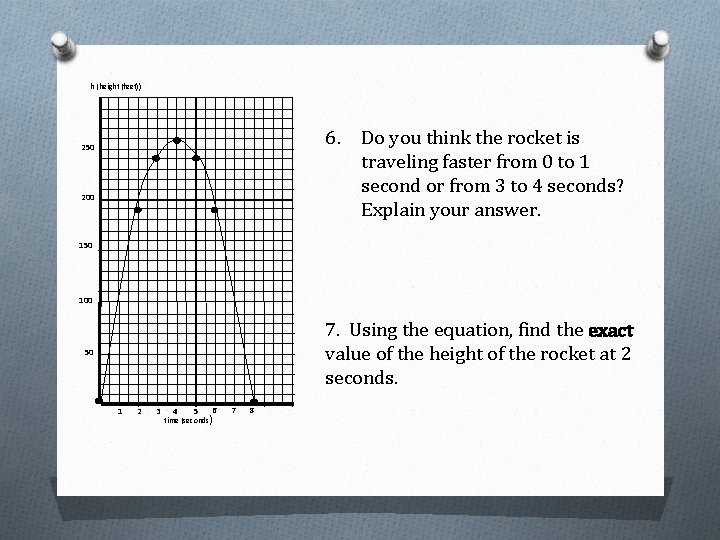
h (height (feet)) 6. Do you think the rocket is traveling faster from 0 to 1 second or from 3 to 4 seconds? Explain your answer. 250 200 150 100 7. Using the equation, find the exact value of the height of the rocket at 2 seconds. 50 1 2 3 4 5 6 time (seconds) 7 8

Things to remember when completing quadratic application word problems: t is time. This is how long the object travels h or d is distance or height the object travels When an object hits the ground, what is it’s height?

Example 4: After t seconds, a ball tossed in the air from the ground level reaches a height of h feet given by the equation h = 144 t – 16 t 2. a. What is the height of the ball after 3 second? b. What is the maximum height the ball will reach? c. Find the number of seconds the ball is in the air when it reaches a height of 224 feet. d. After how many seconds will the ball hit the ground before rebound?

Example 5: A rocket carrying fireworks is launched from a hill 80 feet above a lake. The rocket will fall into lake after exploding at its maximum height. The rocket’s height above the surface of the lake is given by h = -16 t 2 + 64 t + 80. a. What is the height of the rocket after 1. 5 second? b. What is the maximum height reached by the rocket? c. How long will it take for the rocket to hit 128 feet? d. After how many seconds after it is launched will the rocket hit the lake? e. How high was the rocket when it was first launched? f. When does the rocket reach the same height that it was when it was first launched?

Example 6 The product of 2 consecutive positive integers is 110. Find the integers

Example 7 The sum of two integers is 18. The sum of the square of the two integers is 164. Find the integers.