Solving Quadratic Equations by FACTORING What are Quadratic

Solving Quadratic Equations by FACTORING

What are Quadratic Equations? A quadratic equation is an equation which: y = x 2 2 + 2 y = x Contains a 2 + x – 4 2 y = x x term y = x 2 + 2 x – 3 All of these equations contain a x 2 term therefore they are called: Quadratic Equations

Which of the following are Quadratic Equations? y=x+3 y= x 2 . . WHY? It Contains a x 2 term y = 2 x – 4 y = x 2 + 2 x – 3 …. WHY? It Contains a x 2 term

Solving Quadratic Equations BY FACTORING Remember: Quadratic Equations Contain a x 2 term There are several methods of solving QUADRATICS but one methods that you must know is called FACTORING “Factors” are the numbers you multiply to get another number The (+) factors of 6 are: 1 x 6 and 2 x 3 The (-) factors of 6 are: -1 x -6 and -2 x -3

Solving Quadratic Equations BY FACTORING BIG IDEA NUMBER ONE If A(B) = 0 what can we say about either A or B? Either A or B must equal ZERO!!! A = 0 or B = 0

Solving Quadratic Equations BY FACTORING BIG IDEA NUMBER ONE So if… (x + 3) (x – 3) = 0 THEN EITHER (x + 3) = 0 or (x – 3) = 0 x = -3 So…. or x=3

Solving Quadratic Equations BY FACTORING BIG IDEA NUMBER ONE TO SOLVE A QUADRATIC EQUATION BY FACTORING • MAKE THE EQUATION EQUAL TO ZERO • FACTOR THE EQUATION • SET THE FACTORS EQUAL TO ZERO AND SOLVE
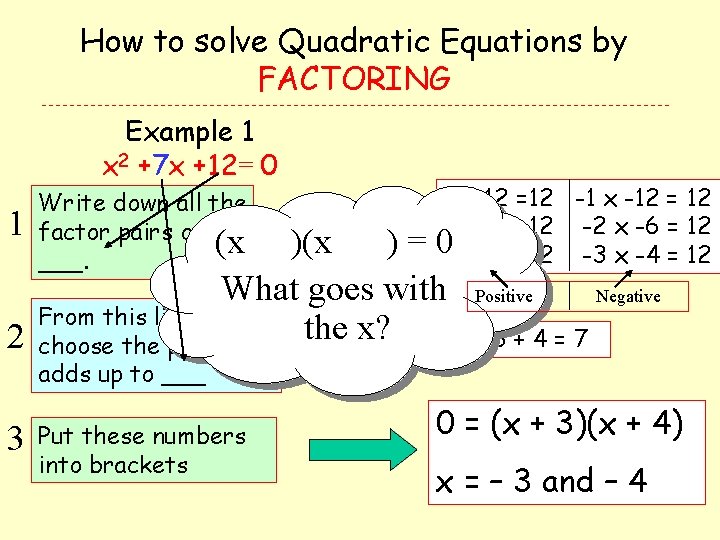
How to solve Quadratic Equations by FACTORING Example 1 x 2 +7 x + 12= 0 1 Write down all the factor pairs of (x ___. 1 x 12 =12 -1 x -12 = 12 2 x 6 = 12 -2 x -6 = 12 03 x 4 = 12 -3 x -4 = 12 )(x )= What goes with From this list, 2 choose the pair that the x? Positive Negative 3+4=7 adds up to ___ 3 Put these numbers into brackets 0 = (x + 3)(x + 4)) x = – 3 and – 4

PROOF: x 2 + 7 x + 12 = (x + 3) (x + 4) Factor: x(x + 4) + 3(x + 4) Factor: x(x) + x(4) + 3(x) + 3(4) Combine like terms: x 2 + 4 x + 3 x + 12 x 2 + 7 x + 12

How to solve Quadratic Equations by FACTORING Example 2 x 2 - 5 x + 6 = 0 1 Write down all the factor pairs of ___. 2 From this list, choose the pair that adds up to ___. 3 Put these numbers into brackets 1 x 6 = 6 -1 x -6 = 6 2 x 3 = 6 -2 x -3 = 6 Positive Negative -2 + -3 = -5 (x - 2)(x - 3) = O x = 2 and 3
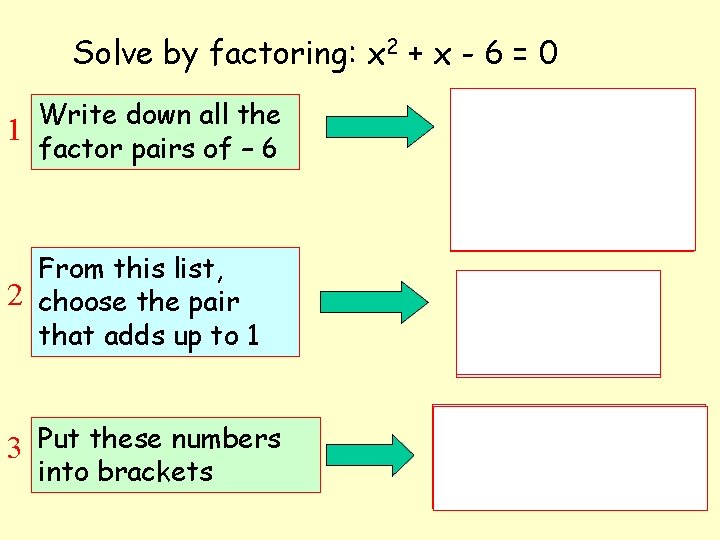
Solve by factoring: x 2 + x - 6 = 0 Write down all the 1 factor pairs of – 6 From this list, 2 choose the pair that adds up to 1 3 Put these numbers into brackets 1 x -6 = -6 2 x -3 = -6 3 x -2 = -6 6 x -1 = -6 (3) + (-2) = 1 3– 2=1 0 = (x + 3)(x - 2) x = – 3 and 2

Copy and fill in the missing values when you factor x 2 +PLEASE 8 x + 12 TAKE = 0 OUT YOUR QUADRATIC EQUATIONS Find all the factor pairs of POWERPOINT 12 1 x 12 =12 -1 x -12 = 12 _____ WORKSHEET 1 -6 = 12 2 x 6 = 12 -2# x WORK TOGETHER FACTOR 3 x 4 = 12 TO-3 x -4 = 12 THE NEXT QUADRATIC From these choose the pair that add up to _____ 8 2+6=8 Put these values into the brackets (x +2 _ )(x +6 _)=0 x = -2 x = -6 USE WORKSHEET #1 x 2 + 3 x + 2 = 0 2 Find all the factor pairs of _____ 1 x 2 = 2 -1 x -2 = 2 From these choose the pair that add up to _____3 1 + 2= 3 Put these values into the brackets 2 =0 (x+ 1_)(x+ _) x 2 + x – 12 = 0 Find all the factor pairs of _____ From these choose the pair that add up to _____ Put these values into the brackets (x + _) = 0 x 2 – 12 x – 20 = 0 Find all the factor pairs of _____ From these choose the pair that add up to _____ Put these values into the brackets (x + _) = 0

1 x 2 + 5 x + 6 = 0 2 3 4 5 6 7 8 x 2 - x – 6 = 0 (x YOUR + 2)(x + 6) x 2 + PLEASE 8 x + 12 TAKE = 0 OUT QUADRATIC x 2 + x – 12 = 0 EQUATIONS (x – 3)(x + 4) POWERPOINT 2 x - 8 x + 15 = 0 (x – 3)(x – 5) WORKSHEET # 2 x 2 + 3 x – 28 = 0 (x + 7)(x – 4) x 2 - 3 x – 18 = 0 (x – 6)(x + 3) x 2 - 10 x – 24 = 0 (x - 12)(x + 2) 9 x 2 + 8 x + 16 = 0 10 (x + 3)(x + 2) (x – 3)(x + 2) x 2 - 6 x – 40 = 0 (x + 4) (x - 10)(x + 4)

1 x 2 + 5 x + 6 = 0 (x + 3)(x + 2) 2 3 4 5 6 7 8 9 (x – 3)(x + 2)(x + 6) (x – 3)(x + 4) (x – 3)(x – 5) (x + 7)(x – 4) (x – 6)(x + 3) 6 and -3 (x - 12)(x + 2) 6 and -3 (x + 4) -4 and -4 (x - 10)(x + 4) - 10 and -4 10 x 2 - x – 6 = 0 x 2 + 8 x + 12 = 0 x 2 + x – 12 = 0 x 2 - 8 x + 15 = 0 x 2 + 3 x – 21 = 0 x 2 - 3 x – 18 = 0 x 2 - 10 x – 24 = 0 x 2 + 8 x + 16 = 0 x 2 - 4 x – 60 = 0 -3 and -2 -2 and -6 3 and -4 3 and 5 -7 and 4

FACTORING SPECIAL QUADRATIC EQUATIONS THE DIFFERENCE BETWEEN PERFECT SQUARES

FACTORING THE DIFFERENCE BETWEEN PERFECT SQUARES (x 2 + 0 x - 4) Is This A Quadratic Equation? FACTORING (x 2 + 0 x - 4) 1 x -4 = -4 1 Find all the factor pairs of - 4 2 x -2 = -4 2 From these choose the pair 2 + -2 = 0 that add up to “ 0” 3 Put these values into the brackets (x + _) = 0 (x + 2)(x - 2) = 0 Notice: x 2 + 0 x – 4 = (x 2 – 4)

FACTORING THE DIFFERENCE BETWEEN PERFECT SQUARES This is often called the “Difference between Two Squares” x 2 – 4 (x + 2)(x – 2)

FACTORING THE DIFFERENCE BETWEEN PERFECT SQUARES TO FACTOR THE DIFFERENCE BETWEEN SQUARES x 2 - 16 1) TAKE THE SQUARE ROOT OF THE BOTH TERMS. x 2 = x 2) MAKE THE BRACKETS { one (+) one (-) } 16 = 4 (x + __ 4 ) (x - __ 4 ) AND FILL IN THE BLANKS. x 2 – 16 = (x + 4 ) (x - 4 ) (x + 4 ) = 0 (x - 4 ) = 0 x = -4 x=4
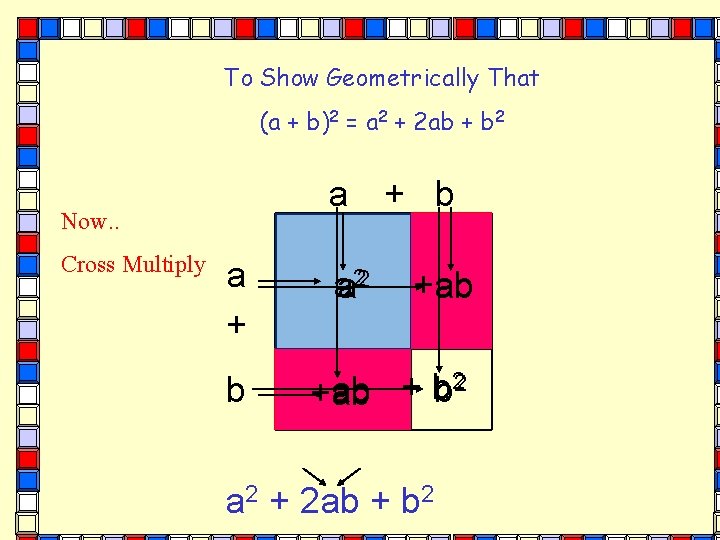
To Show Geometrically That (a + b)2 = a 2 + 2 ab + b 2 a Now. . Cross Multiply a + b a 22 + b +ab ab 2 + b ab +ab a 2 + 2 ab + b 2
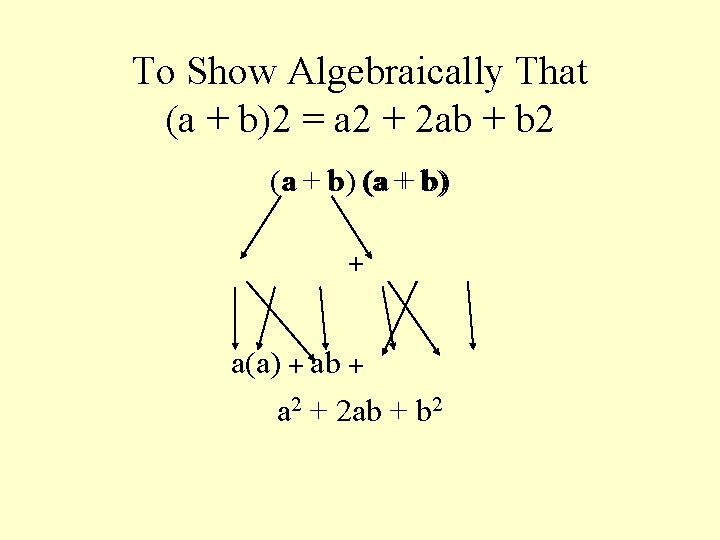
To Show Algebraically That (a + b)2 = a 2 + 2 ab + b 2 (aa + bb) (a + b) + a(a) + ab + a 2 + 2 ab + b 2
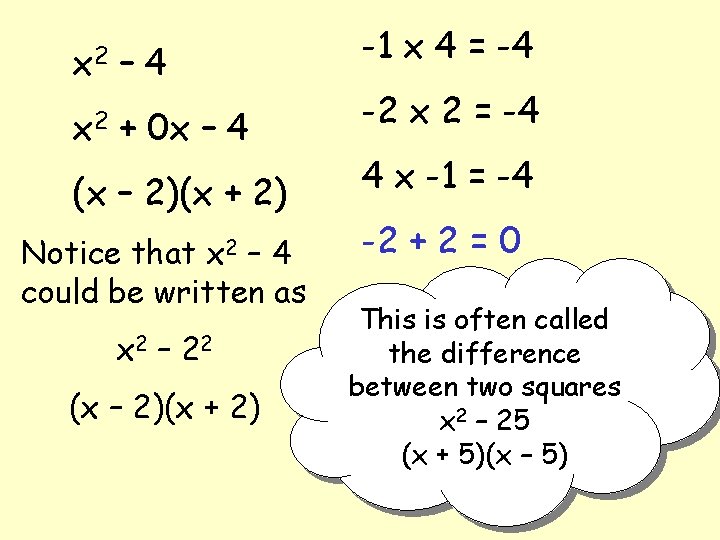
x 2 – 4 x 2 + 0 x – 4 (x – 2)(x + 2) Notice that x 2 – 4 could be written as x 2 – 2 2 (x – 2)(x + 2) -1 x 4 = -4 -2 x 2 = -4 4 x -1 = -4 -2 + 2 = 0 This is often called the difference between two squares x 2 – 25 (x + 5)(x – 5)
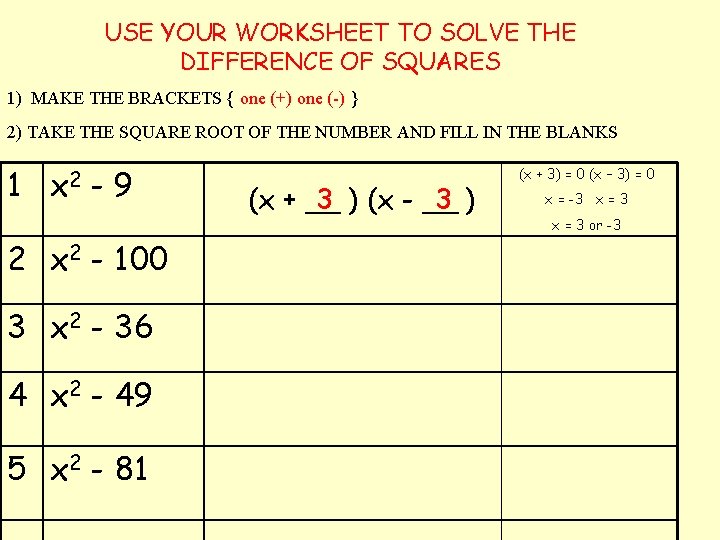
USE YOUR WORKSHEET TO SOLVE THE DIFFERENCE OF SQUARES 1) MAKE THE BRACKETS { one (+) one (-) } 2) TAKE THE SQUARE ROOT OF THE NUMBER AND FILL IN THE BLANKS 1 x 2 -9 2 x 2 - 100 3 x 2 - 36 4 x 2 - 49 5 x 2 - 81 (x + __ 3 ) (x - __ 3 ) (x + 3) = 0 (x – 3) = 0 x = -3 x = 3 or -3

1 2 3 4 5 6 7 8 x 2 - 9 x 2 - 100 x 2 - 36 x 2 - 49 x 2 - 81 x 2 - 64 x 2 - 18 x 2 - 24 (x + 3)(x – 3) (x + 10)(x – 10) (x + 6)(x – 6) (x + 7)(x – 7) (x + 9)(x – 9) (x + 8)(x – 8) (x + √ 18)(x – √ 18) (x + √ 24)(x – √ 24)
(x ) What goes with the x?

(x + 3)(x + 2) You try (x + 5)(x + 2) x(x + 2) + 3(x + 2) (x – 2)(x + 3) (x + 2)(x – 4) (x + + 3)(x + 4)+ 3 X (x + 2) (x – 3)(x – 2) x X=(x 2) x. Xx+x. X 2+3 Xx+3 X 2 x 2 + 2 x + 3 x + 6 x 2 + 5 x + 6

PROOF: x 2 - 5 x + 6 = (x - 3) (x - 2) Factor: Combine like terms: x(x - 2) -3(x - 2) x(x) + x(-2) - 3(x) - 3(-2) x 2 - 2 x - 3 x + 6 x 2 - 5 x + 6
- Slides: 26