Solving Quadratic Equations An explanation by Molly Murphy

Forms of Quadratics • Standard Form • ƒ(x) = ax² + bx + c • Vertex Form • ƒ(x) = a(x - h)² + k • Intercept Form • ƒ(x) = a(x - p)(x - q)

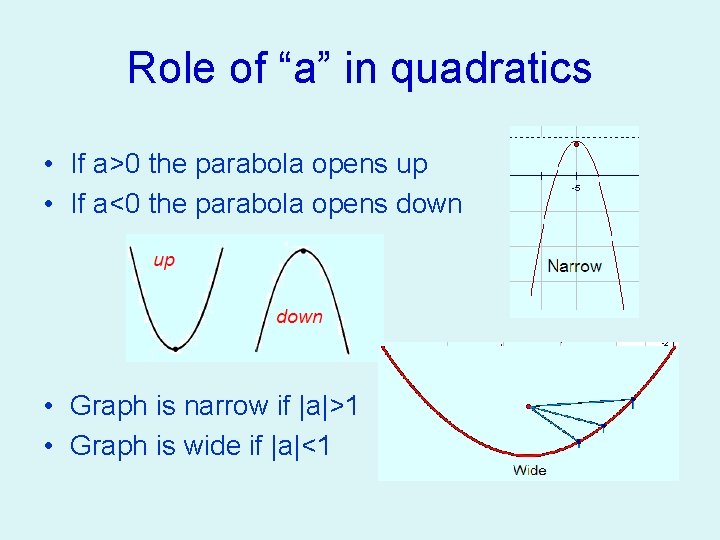
Role of “a” in quadratics • If a>0 the parabola opens up • If a<0 the parabola opens down • Graph is narrow if |a|>1 • Graph is wide if |a|<1

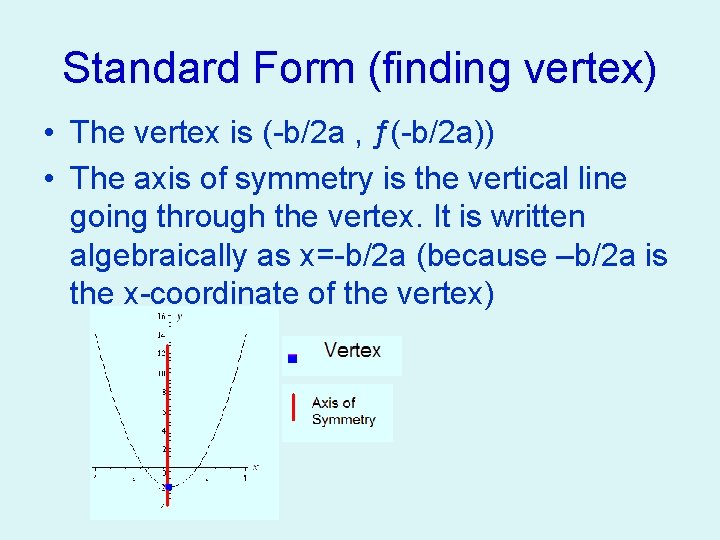
Standard Form (finding vertex) • The vertex is (-b/2 a , ƒ(-b/2 a)) • The axis of symmetry is the vertical line going through the vertex. It is written algebraically as x=-b/2 a (because –b/2 a is the x-coordinate of the vertex)

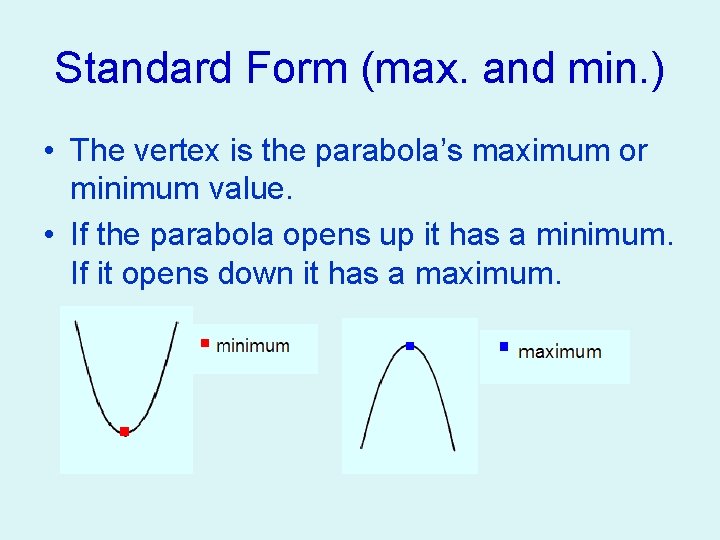
Standard Form (max. and min. ) • The vertex is the parabola’s maximum or minimum value. • If the parabola opens up it has a minimum. If it opens down it has a maximum.

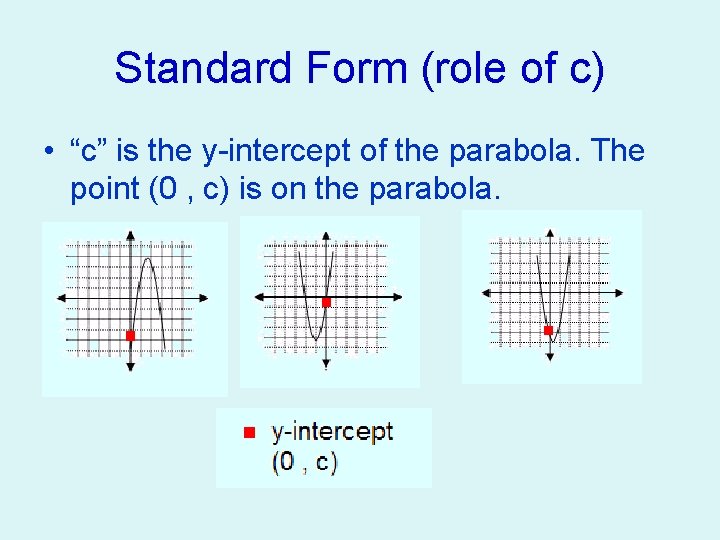
Standard Form (role of c) • “c” is the y-intercept of the parabola. The point (0 , c) is on the parabola.

Graphing in Standard form • Example: ƒ(x) = 2 x² + 4 x + 1 • Find the x-coordinate of the vertex -b/2 a = -4/2(2) = -4/4= -1 • Plug that number back into the function to find the y -coordinate 2(-1)²+4(-1)+1 = -2²-4+1 = 2 -4+1 = -1 • The vertex is (-1 , -1) • Make a chart with other values on either “side” of the x-coordinate of the vertex. Plug the x values into the function to get the y values. X -3 -2 -1 0 1 Y 7 1 -1 1 7

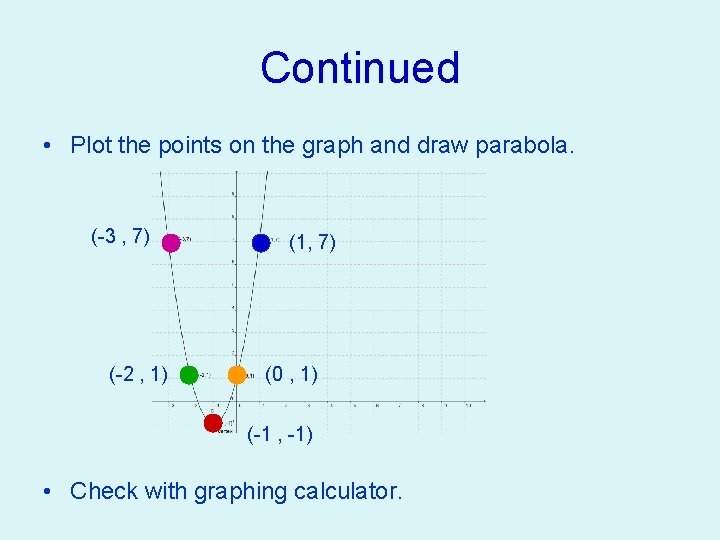
Continued • Plot the points on the graph and draw parabola. (-3 , 7) (-2 , 1) (1, 7) (0 , 1) (-1 , -1) • Check with graphing calculator.

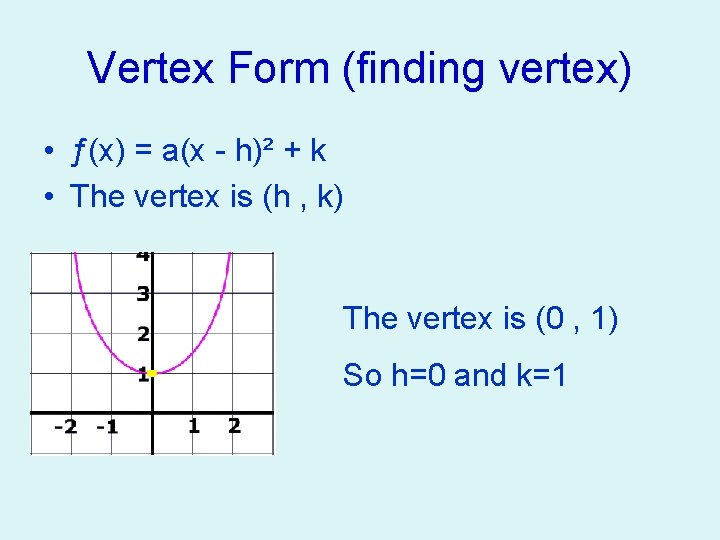
Vertex Form (finding vertex) • ƒ(x) = a(x - h)² + k • The vertex is (h , k) The vertex is (0 , 1) So h=0 and k=1

Graphing in Vertex Form • ƒ(x) = 2(x + 1)² - 1 • We already know the vertex is (-1 , -1) • Make a chart of x and y values. Plug the x values into the equation and solve to get the y values. X -3 -2 -1 0 1 Y 7 1 -1 1 7

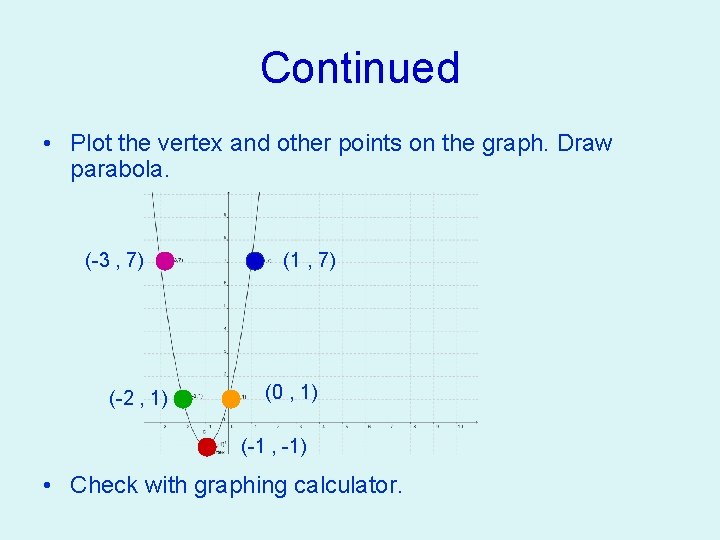
Continued • Plot the vertex and other points on the graph. Draw parabola. (-3 , 7) (-2 , 1) (1 , 7) (0 , 1) (-1 , -1) • Check with graphing calculator.

Intercept Form (finding vertex) • ƒ(x) = a(x – p)(x – q) • For the x-coordinate of the vertex, average p and q (p+q)/2. For the y-coordinate of the vertex, plug that value back into the function. ƒ((p+q)/2).

Graphing in Intercept Form • ƒ(x) = a(x – p)(x – q) • The x-intercepts are p and q. • ƒ(x) = 2(x + 3)(x + 1) • Plot the vertex (-3+-1)/2 = -4/2 = -2 y = 2(-2+3)(-2+1) = -2 the vertex is (-2 , -2) • Next plot the x-intercepts (0 , -3) and (0 , -1) • Draw in parabola.

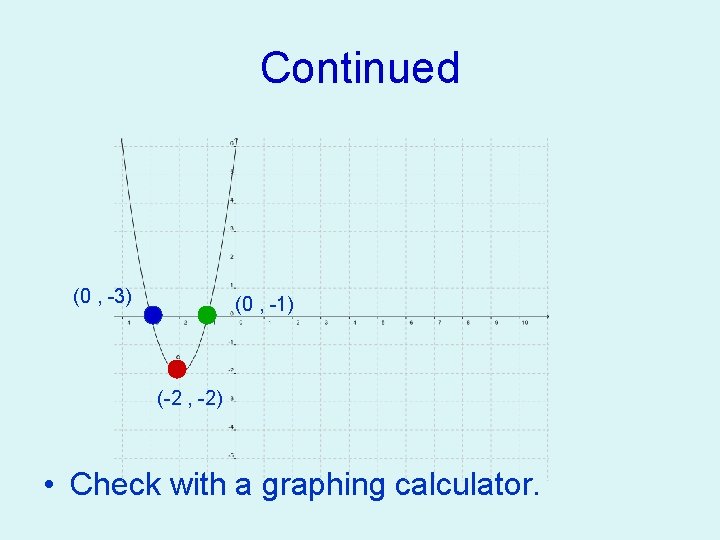
Continued (0 , -3) (0 , -1) (-2 , -2) • Check with a graphing calculator.