Solving Quadratic Equations 8 7 by Using Square

Solving Quadratic Equations 8 -7 by Using Square Roots Warm Up Lesson Presentation Lesson Quiz Holt Mc. Dougal Algebra 1 Algebra 11 Holt Mc. Dougal

Solving Quadratic Equations 8 -7 by Using Square Roots Objective Solve quadratic equations by using square roots. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Example 1 A: Using Square Roots to Solve x 2 = a Solve using square roots. Check your answer. x 2 = 169 Solve for x by taking the square root of both sides. Use ± to show both square roots. x = ± 13 The solutions are 13 and – 13. x 2 = 169 Substitute 13 and – 13 (– 13)2 169 into the original 169 169 equation. Check x 2 = 169 (13)2 169 Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Example 1 B: Using Square Roots to Solve x 2 = a Solve using square roots. x 2 = – 49 There is no real number whose square is negative. There is no real solution. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Check It Out! Example 1 a Solve using square roots. Check your answer. x 2 = 121 Solve for x by taking the square root of both sides. Use ± to show both x = ± 11 square roots. The solutions are 11 and – 11. x 2 = 121 Check x 2 = 121 (11)2 121 Substitute 11 and – 11 (– 11)2 121 into the original 121 121 equation. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Example 2 A: Using Square Roots to Solve Quadratic Equations Solve using square roots. x 2 + 7 = 7 – 7 x 2 = 0 The solution is 0. Holt Mc. Dougal Algebra 1 Subtract 7 from both sides. Take the square root of both sides.

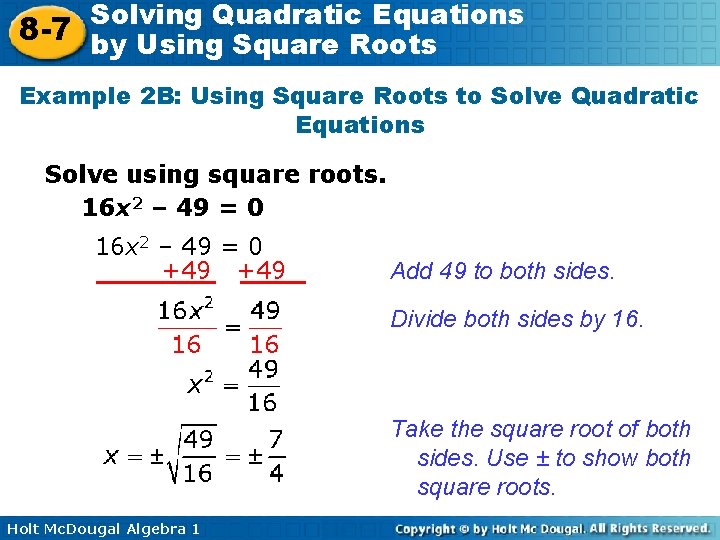
Solving Quadratic Equations 8 -7 by Using Square Roots Example 2 B: Using Square Roots to Solve Quadratic Equations Solve using square roots. 16 x 2 – 49 = 0 +49 Add 49 to both sides. Divide both sides by 16. Take the square root of both sides. Use ± to show both square roots. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Check It Out! Example 2 b Solve by using square roots. Check your answer. (x – 5)2 = 16 x – 5 = ± 4 Take the square root of both sides. Use ± to show both square roots. x – 5 = 4 or x – 5 = – 4 Write two equations, using both the positive and negative square roots, +5+5 +5 +5 and solve each equation. x = 9 or x = 1 The solutions are 9 and 1. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Example 3 A: Approximating Solutions Solve. Round to the nearest hundredth. x 2 = 15 Take the square root of both sides. x 3. 87 Evaluate on a calculator. The approximate solutions are 3. 87 and – 3. 87. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Example 3 B: Approximating Solutions Solve. Round to the nearest hundredth. – 3 x 2 + 90 = 0 – 90 Subtract 90 from both sides. Divide by – 3 on both sides. x 2 = 30 Take the square root of both sides. x 5. 48 Evaluate on a calculator. The approximate solutions are 5. 48 and – 5. 48. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Check It Out! Example 3 a Solve. Round to the nearest hundredth. 0 = 90 – x 2 Add x 2 to both sides. 0 = 90 – x 2 + x 2 = 90 Take the square root of both sides. The approximate solutions are 9. 49 and – 9. 49. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Check It Out! Example 3 b Solve. Round to the nearest hundredth. 2 x 2 – 64 = 0 + 64 Add 64 to both sides. Divide by 2 on both sides. x 2 = 32 Take the square root of both sides. The approximate solutions are 5. 66 and – 5. 66. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Check It Out! Example 3 c Solve. Round to the nearest hundredth. x 2 + 45 = 0 – 45 x 2 = – 45 Subtract 45 from both sides. There is no real number whose square is negative. There is no real solution. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Example 4: Application Ms. Pirzada is building a retaining wall along one of the long sides of her rectangular garden. The garden is twice as long as it is wide. It also has an area of 578 square feet. What will be the length of the retaining wall? Let x represent the width of the garden. lw = A l = 2 w 2 x x = 578 2 x 2 = 578 Holt Mc. Dougal Algebra 1 Use the formula for area of a rectangle. Length is twice the width. Substitute x for w, 2 x for l, and 578 for A.

Solving Quadratic Equations 8 -7 by Using Square Roots Example 4 Continued 2 x 2 = 578 Divide both sides by 2. Take the square root of both sides. x = ± 17 Evaluate on a calculator. Negative numbers are not reasonable for width, so x = 17 is the only solution that makes sense. Therefore, the length is 2 w or 34 feet. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Check It Out! Example 4 A house is on a lot that is shaped like a trapezoid. The solid lines show the boundaries, where x represents the width of the front yard. Find the width of the front yard, given that the area is 6000 square feet. Round to the nearest foot. (Hint: Use ) 2 x 2 x x Use the formula for area of a trapezoid. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Check It Out! Example 4 Substitute 2 x for h and b 1, x for b 2 , and 6000 for A. Divide by 3 on both sides. Take the square root of both sides. Evaluate on a calculator. Negative numbers are not reasonable for width, so x ≈ 45 is the only solution that makes sense. Therefore, the width of the front yard is about 45 feet. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -7 by Using Square Roots Lesson Quiz: Part II 5. A community swimming pool is in the shape of a trapezoid. The height of the trapezoid is twice as long as the shorter base and the longer base is twice as long as the height. The area of the pool is 3675 square feet. What is the length of the longer base? Round to the nearest foot. (Hint: Use 108 feet Holt Mc. Dougal Algebra 1 )