Solving Quadratic Equation by Graphing Section 6 1

Solving Quadratic Equation by Graphing Section 6. 1

Quadratic Equation y = ax 2 + bx + c 2 ax is the quadratic term. bx is the linear term. c is the constant term. The highest exponent is two; therefore, the degree is two.

Identifying Terms 2 Example f(x)=5 x -7 x+1 Quadratic term 5 x 2 Linear term -7 x Constant term 1

Identifying Terms 2 Example f(x) = 4 x - 3 Quadratic term Linear term Constant term 4 x 0 -3 2

Identifying Terms Now you try this problem. 2 f(x) = 5 x - 2 x + 3 quadratic term linear term constant term 5 x 2 -2 x 3
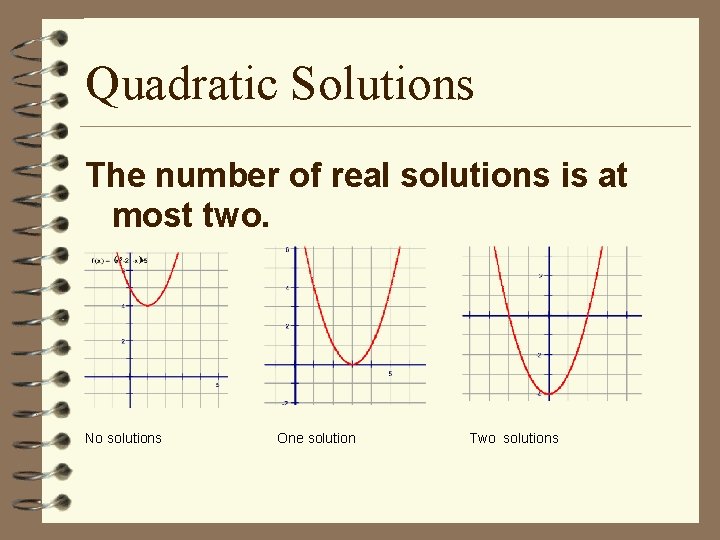
Quadratic Solutions The number of real solutions is at most two. No solutions One solution Two solutions

Solving Equations When we talk about solving these equations, we want to find the value of x when y = 0. These values, where the graph crosses the x-axis, are called the x-intercepts. These values are also referred to as solutions, zeros, or roots.
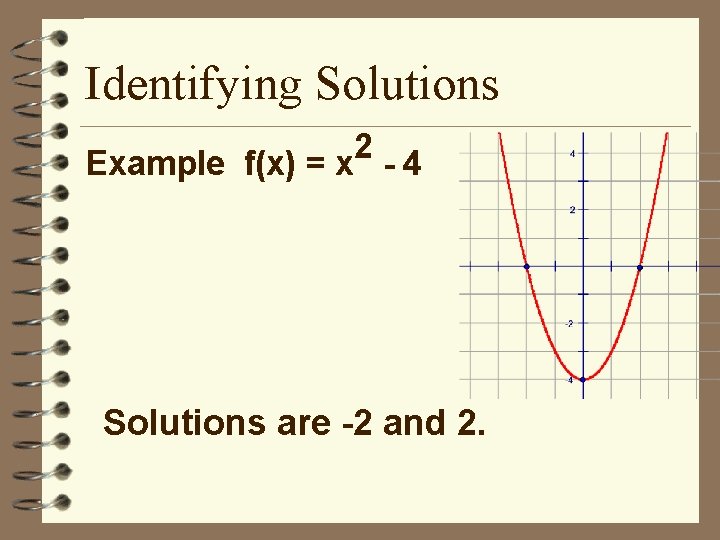
Identifying Solutions 2 Example f(x) = x - 4 Solutions are -2 and 2.
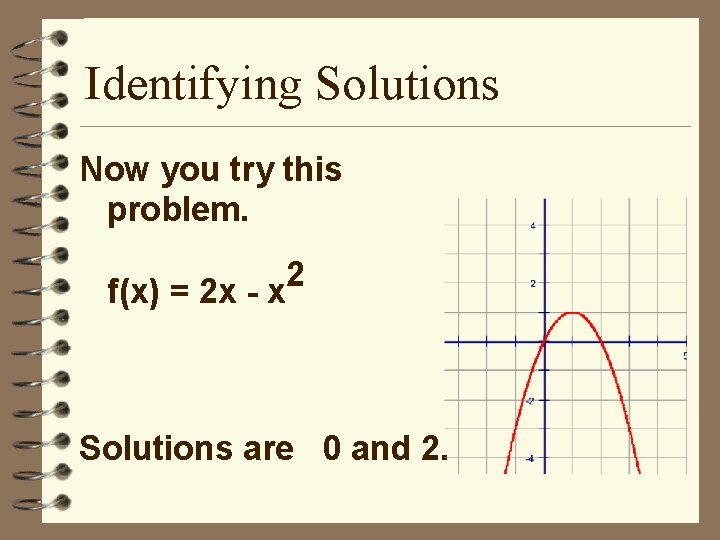
Identifying Solutions Now you try this problem. f(x) = 2 x - x 2 Solutions are 0 and 2.

Graphing Quadratic Equations The graph of a quadratic equation is a parabola. The roots or zeros are the xintercepts. The vertex is the maximum or minimum point. All parabolas have an axis of symmetry.
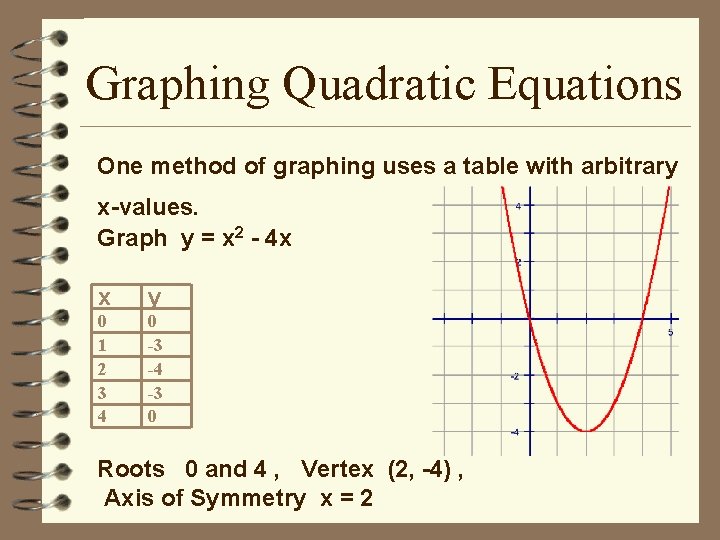
Graphing Quadratic Equations One method of graphing uses a table with arbitrary x-values. Graph y = x 2 - 4 x x y 0 1 2 3 4 0 -3 -4 -3 0 Roots 0 and 4 , Vertex (2, -4) , Axis of Symmetry x = 2
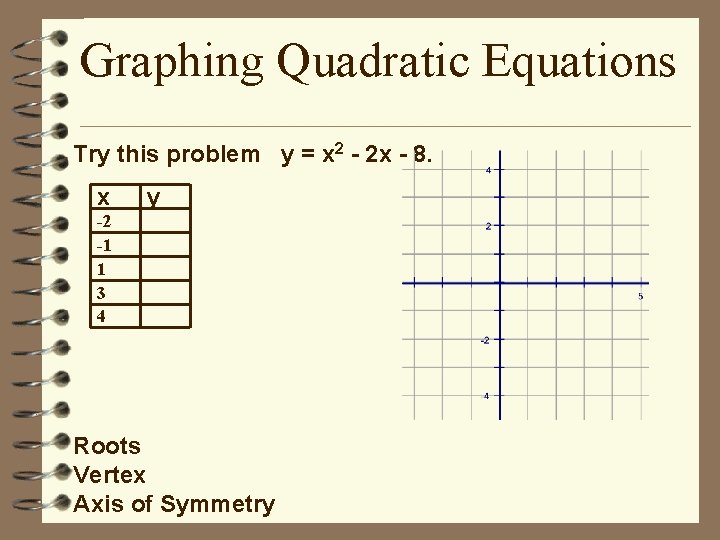
Graphing Quadratic Equations Try this problem y = x 2 - 2 x - 8. x y -2 -1 1 3 4 Roots Vertex Axis of Symmetry

Graphing Quadratic Equations The graphing calculator is also a helpful tool for graphing quadratic equations. Refer to classwork 1 for directions for graphing quadratic equations on the Casio.
- Slides: 13