Solving Quadratic Equation by Graphing and Factoring Section

Solving Quadratic Equation by Graphing and Factoring Section 6. 2& 6. 3 CCSS: A. REI. 4 b

Mathematical Practices: 1. Make sense of problems and persevere in solving 4 4 4 4 them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning.

CCSS: A. REI. 4 b 4 SOLVE quadratic equations by inspection (e. g. , for x 2 = 49), taking square roots, completing the square, the quadratic formula and factoring, as appropriate to the initial form of the equation. RECOGNIZE when the quadratic formula gives complex solutions and write them as a ± bi for real numbers a and b.

Essential Question: 4 How do I determine the domain, range, maximum, minimum, roots, and y-intercept of a quadratic function from its graph & how do I solve quadratic functions by factoring?

Quadratic Equation y = ax 2 + bx + c 2__ ax is the quadratic term. bx--- is the linear term. c-- is the constant term. The highest exponent is two; therefore, the degree is two.

Identifying Terms 2 Example f(x)=5 x -7 x+1 Quadratic term 5 x 2 Linear term -7 x Constant term 1

Identifying Terms 2 Example f(x) = 4 x - 3 Quadratic term 4 x Linear term 0 Constant term -3 2

Identifying Terms Now you try this problem. 2 f(x) = 5 x - 2 x + 3 quadratic term linear term constant term 5 x 2 -2 x 3
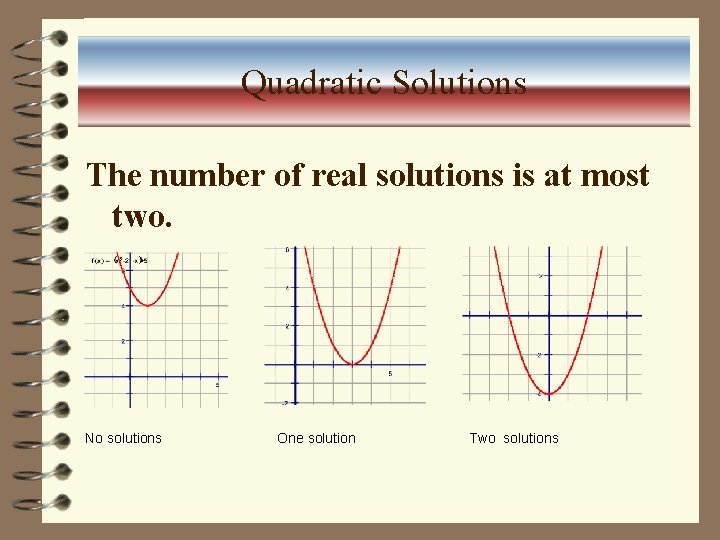
Quadratic Solutions The number of real solutions is at most two. No solutions One solution Two solutions

Solving Equations When we talk about solving these equations, we want to find the value of x when y = 0. These values, where the graph crosses the x-axis, are called the x-intercepts. These values are also referred to as solutions, zeros, or roots.
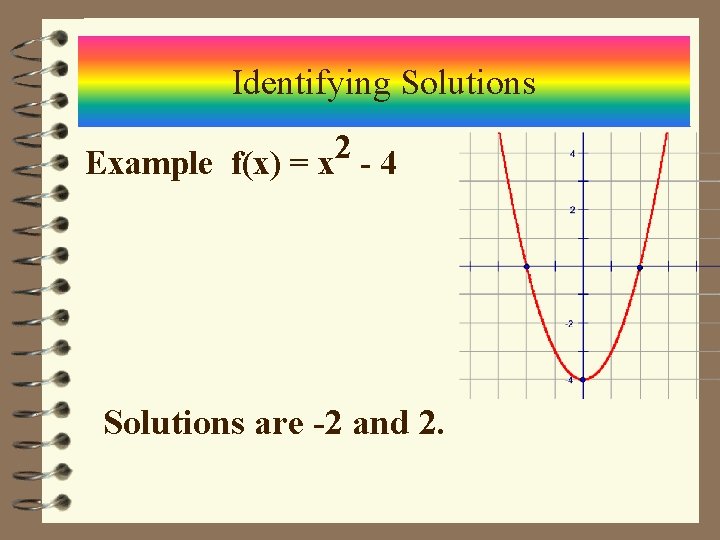
Identifying Solutions 2 Example f(x) = x - 4 Solutions are -2 and 2.
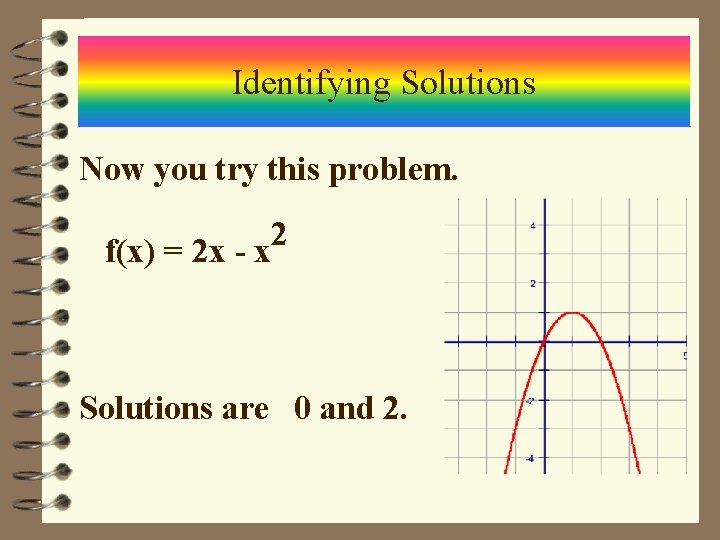
Identifying Solutions Now you try this problem. f(x) = 2 x - x 2 Solutions are 0 and 2.

Graphing Quadratic Equations Ø The graph of a quadratic equation is a parabola. Ø The roots or zeros are the x-intercepts. Ø The vertex is the maximum or minimum point. Ø All parabolas have an axis of symmetry.

Graphing Quadratic Equations One method of graphing uses a table with arbitrary x-values. Graph y = x 2 - 4 x x y 0 1 2 3 4 0 -3 -4 -3 0 Roots 0 and 4 , Vertex (2, -4) , Axis of Symmetry x = 2
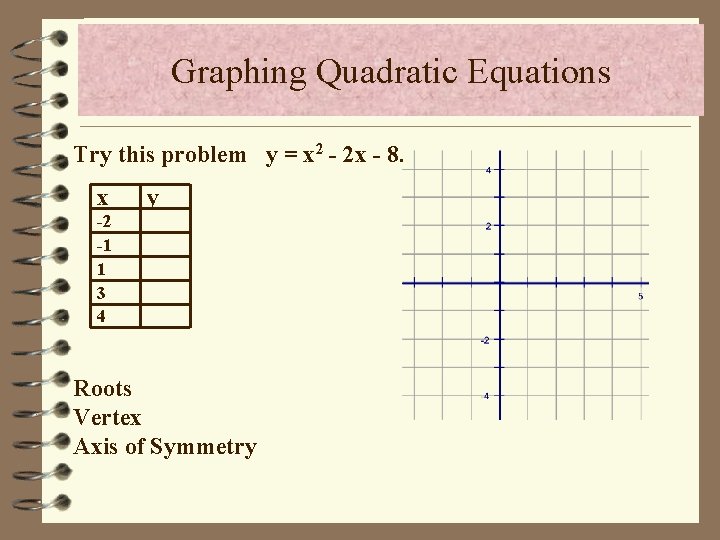
Graphing Quadratic Equations Try this problem y = x 2 - 2 x - 8. x y -2 -1 1 3 4 Roots Vertex Axis of Symmetry

Graphing Quadratic Equations The graphing calculator is also a helpful tool for graphing quadratic equations.

Roots or Zeros of the Quadratic Equation Ø The Roots or Zeros of the Quadratic Equation are the points where the graph hits the x axis. Ø The zeros of the functions are the input that make the equation equal zero. Roots are 4, -3

To solve a Quadratic Equation Make one side zero. Then factor then set each factor to zero
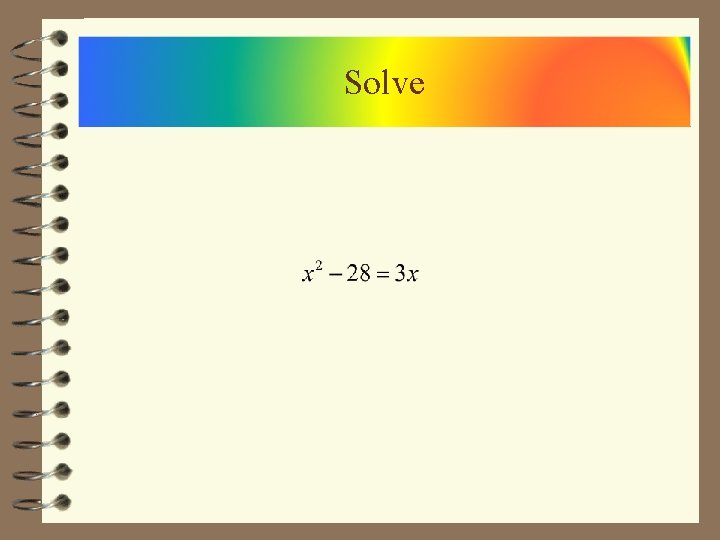
Solve
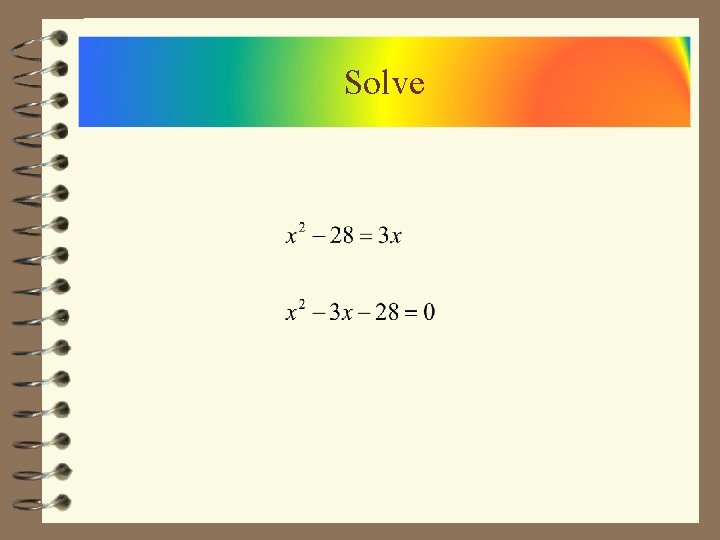
Solve
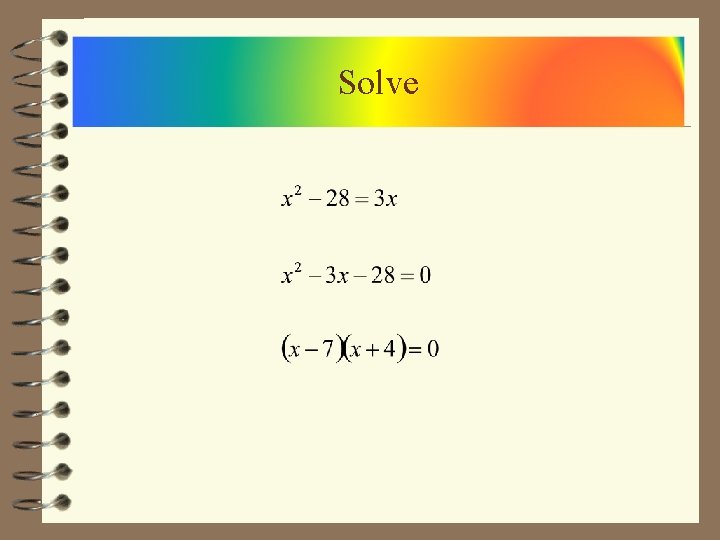
Solve
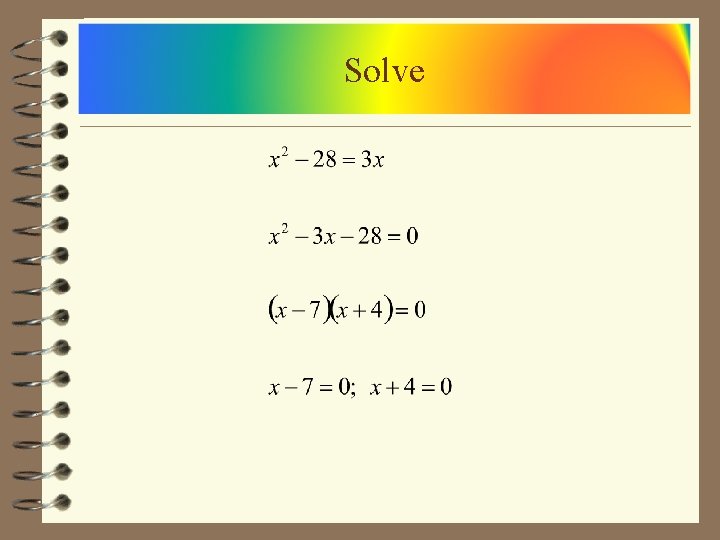
Solve
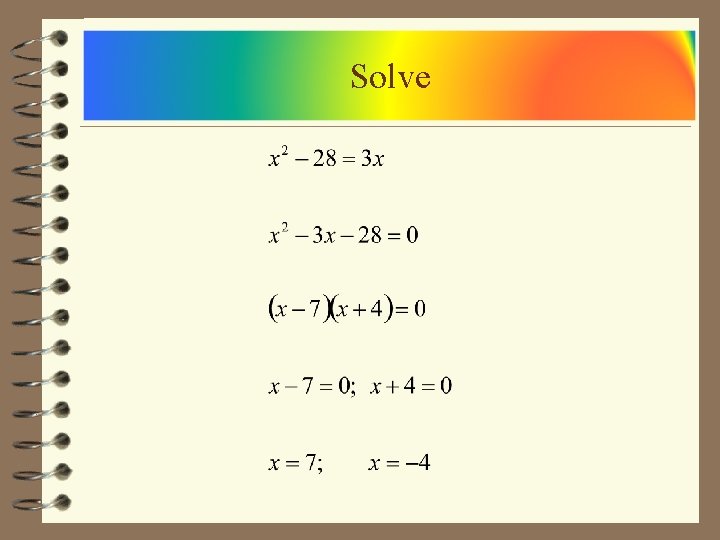
Solve
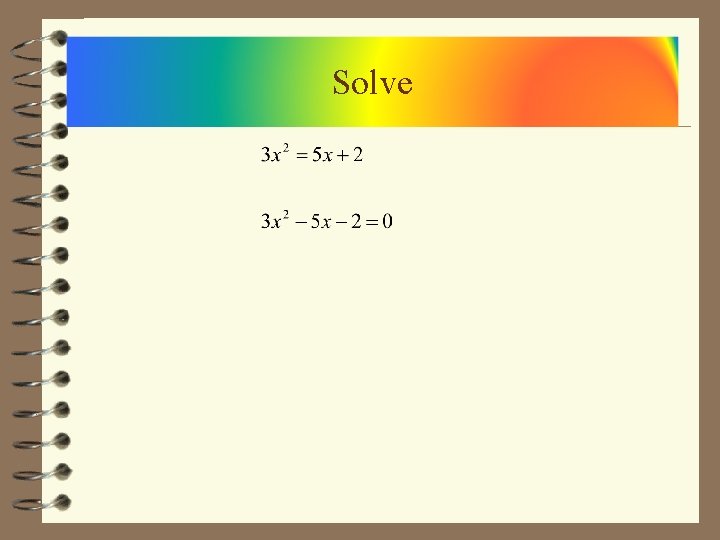
Solve

Solve Multiply the ends together and find what adds to the coefficient of the middle term
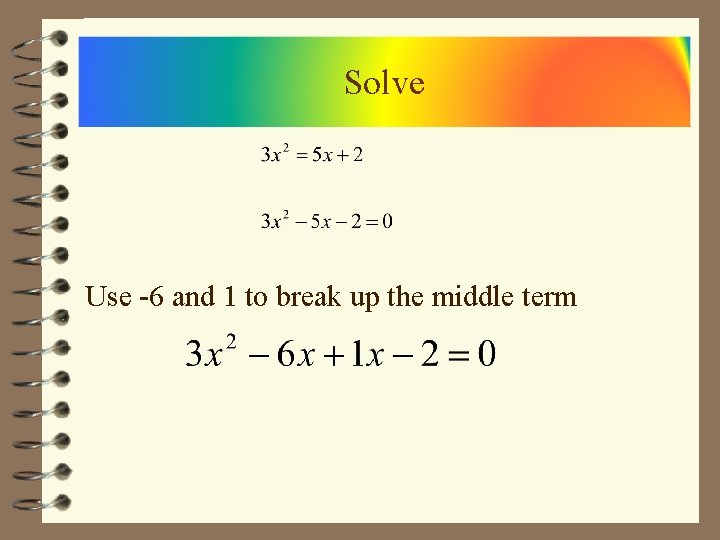
Solve Use -6 and 1 to break up the middle term
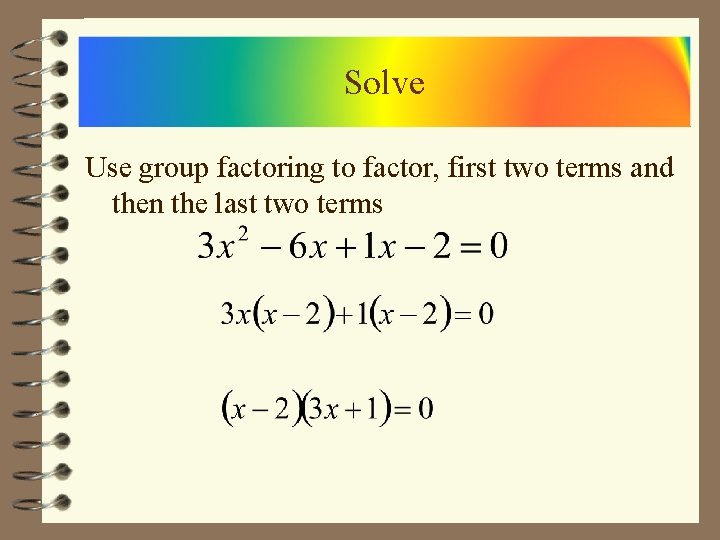
Solve Use group factoring to factor, first two terms and then the last two terms
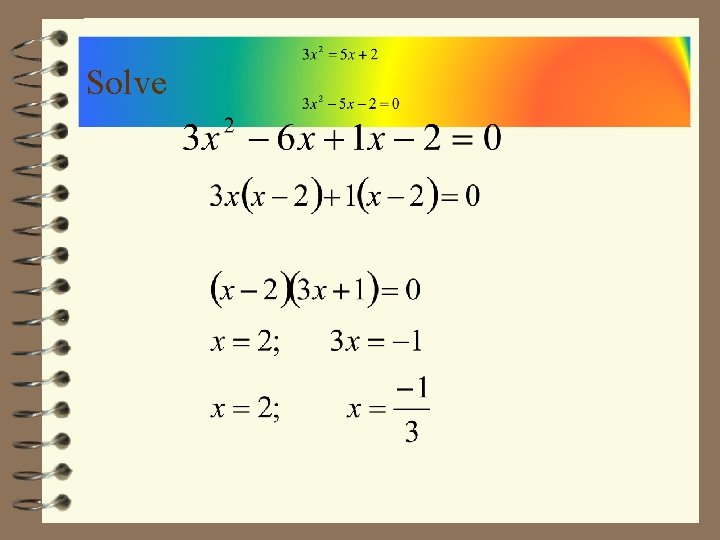
Solve

How to write a quadratic equation with roots Given r 1, r 2 the equation is (x - r 1)(x - r 2)=0 Then foil the factors, x 2 - (r 1 + r 2)x+(r 1· r 2)=0

How to write a quadratic equation with roots Given r 1, r 2 the equation is (x - r 1)(x - r 2)=0 Then foil the factors, x 2 - (r 1 + r 2)x+(r 1· r 2)=0 Roots are -2, 5 Equation x 2 - (-2+5)x+(-2)(5)=0 x 2 - 3 x -10 = 0

How to write a quadratic equation with roots Roots are ¼, 8 Equation x 2 -(¼+8)x+(¼)(8)=0 x 2 -(33/4)x + 2 = 0 Must get rid of the fraction, multiply by the common dominator. 4 4 x 2 - 33 x + 8 = 0
- Slides: 31