Solving One Step Equations S W B A

Solving One. Step Equations

S. W. B. A. T � Students will be able to take their knowledge of order of operations and substitution to solve a one step equation
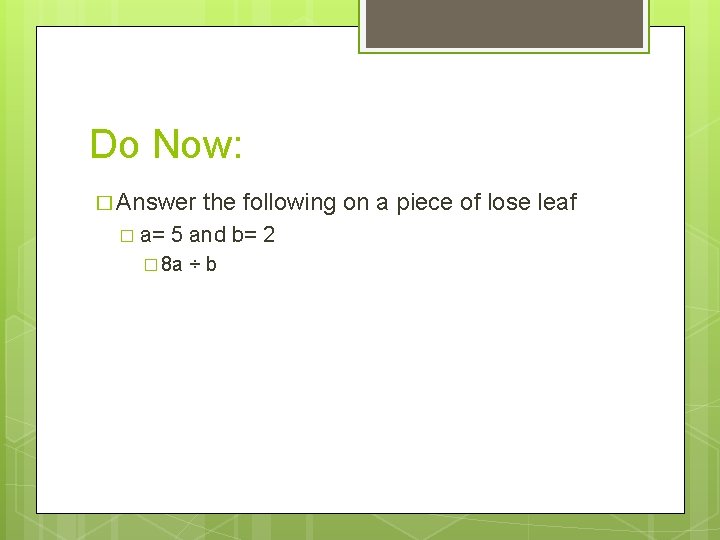
Do Now: � Answer � a= the following on a piece of lose leaf 5 and b= 2 � 8 a ÷b

Solving Equations � In an equation, the variable represents the number that satisfies the equation � To solve an equation means to find the value of the variable that makes the equation true

Process of Solving an Equation � The process of solving an equation involves isolating the variable, making it have a coefficient of 1, on one side of the equation

Addition property of equality � If an equation is true and the same number is added to each side of the equation, the resulting equivalent equation is also true � For any real numbers a, b and c, if a=b, then a +c=b+c

Examples � Solve by adding �C – 22 + 54 � Since we are subtracting 22 from c, we must add 22 to get c by itself. � What we do to the left side we must do to the right side � C – 22 + 22 = 54 + 22 � C = 76 � This is the horizontal method, I will show you the vertical method on the board

Check �C �C = 76 – 22 = 54 � 54 = 54

Subtraction Property of Equality � If an equation is true and the same number is subtracted from each side of the equation, the resulting equivalent equation is also true � For any real numbers a, b and c, if a = b, then a–c=b-c

Examples � Solve by subtracting � 63 + m = 79 � 63 is being added to m, in order to isolate the variable we must subtract 63 from each side � 63 – 63 + m = 79 – 63 � M = 16

Check �m = 16 � 63 + m = 79 � 63 + 16 = 79 � 79 = 79

Multiplication Property of Equality � If an equation is true and each side is multiplied by the same nonzero number, the resulting equation is equivalent � For any real numbers a, b and c, if a = b, then ac = bc

Examples � Solve by multiplying � Take the fraction being multiplied by the variable and multiply each side by its reciprocal

Division Property of Equality � If an equation is true and each side is divided by the same nonzero number, the resulting equation is equivalent � For any real numbers a, b and c, if a = b, then

Examples � Solve by dividing � 39 = -3 r � Since we want r is being multiplied by -3 and we want r to be by itself we must divide each side by -3 � 39 = -3 r -------3 -3 -13 = r

Check � -13 =r � 39 = -3 ( -13) � 39 = 39
- Slides: 16