Solving ODE by artificial neural networks ANNs with

Solving ODE by artificial neural networks (ANNs) -- with Knet. jl and Optim. jl Jiawei Zhuang (jiaweizhuang@g. harvard. edu) School of Engineering and Applied Science, Harvard University

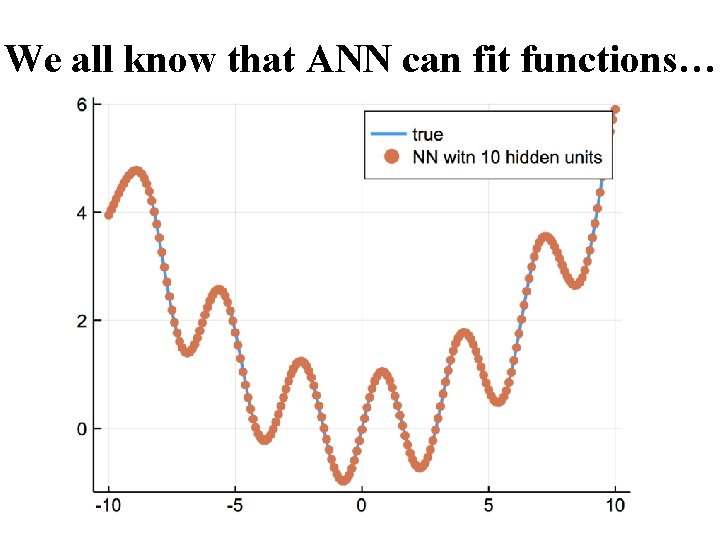
We all know that ANN can fit functions…

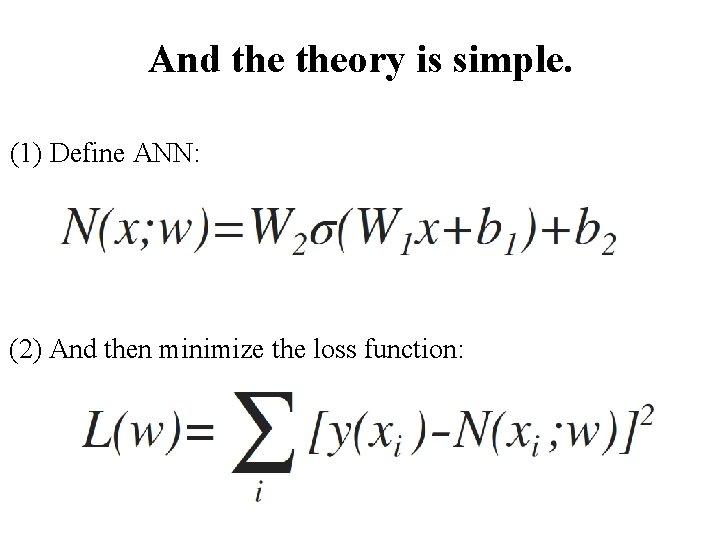
And theory is simple. (1) Define ANN: (2) And then minimize the loss function:

How about ODEs? (1) The standard ANN won’t even satisfy the initial condition. (2) But we can modify it so the initial condition is always right: (3) And then minimize the loss function:

I found an existing project, but it is clearly NOT working! URL: https: //julialang. org/blog/2017/10/gsoc-Neural. Net. Diff. Eq

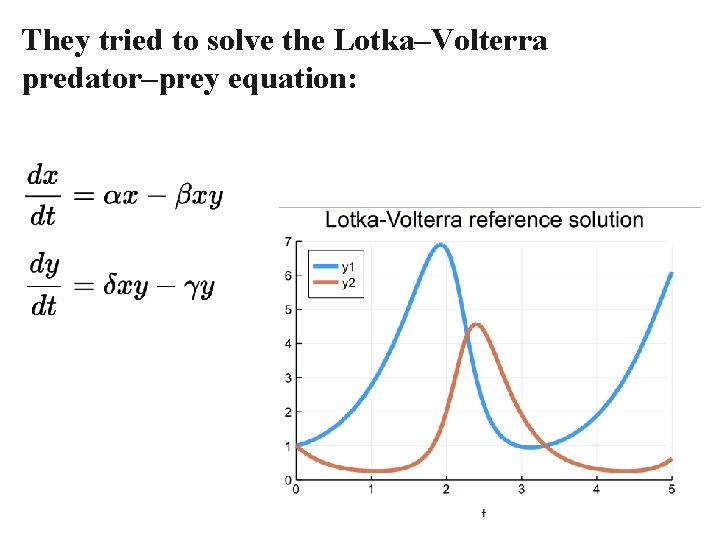
They tried to solve the Lotka–Volterra predator–prey equation:

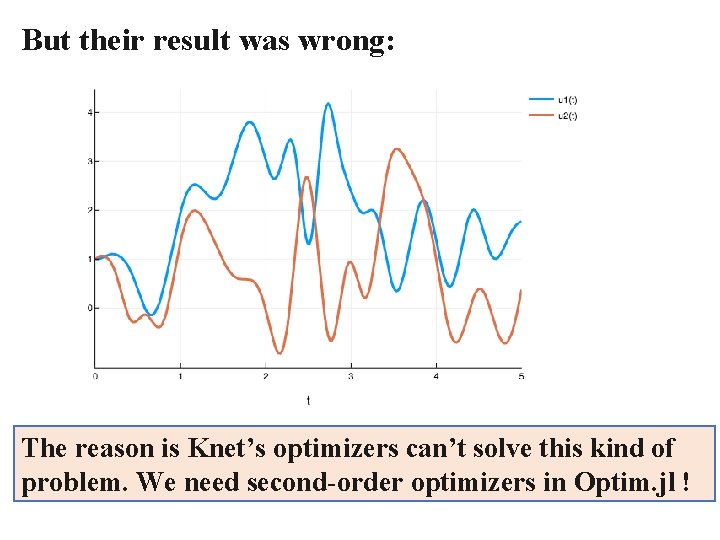
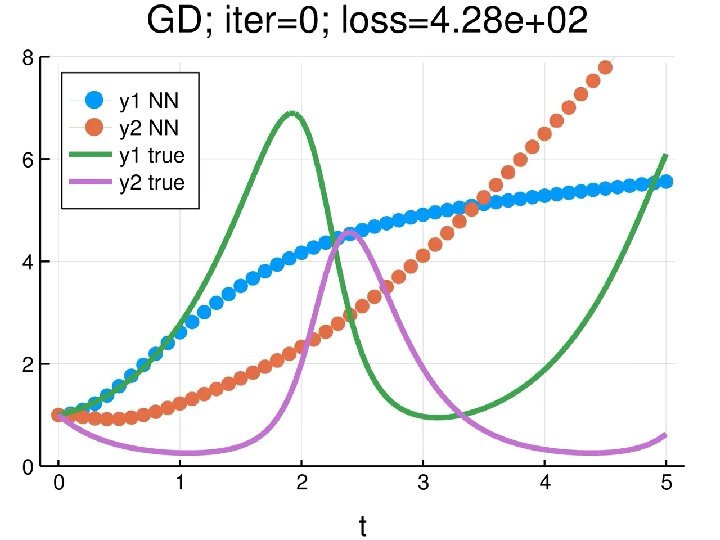
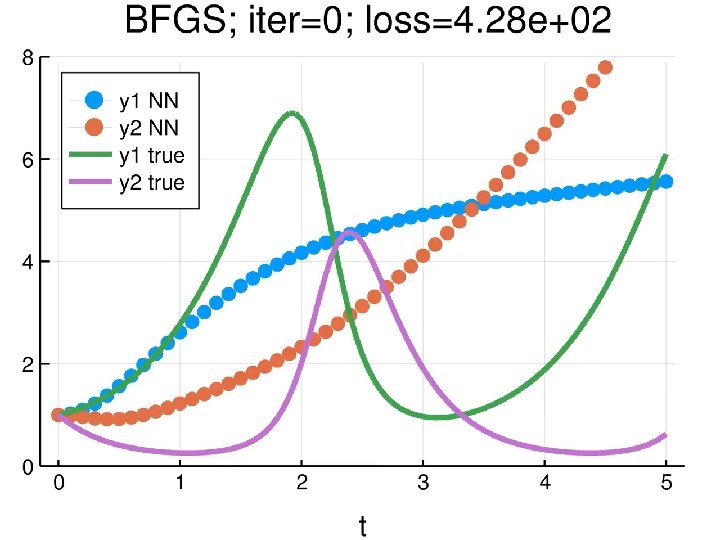
But their result was wrong: The reason is Knet’s optimizers can’t solve this kind of problem. We need second-order optimizers in Optim. jl !

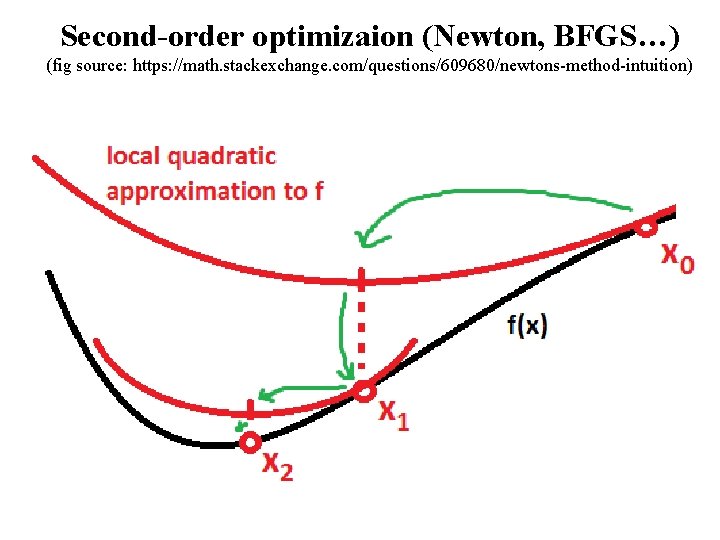
Second-order optimizaion (Newton, BFGS…) (fig source: https: //math. stackexchange. com/questions/609680/newtons-method-intuition)

Advantages of ANN solutions 1. In analytical, closed form; don’t need interpolation to get intermediate points. 2. Differentiable; don’t need finite-difference to get the derivative 3. Represented by NN weights; require less memory/storage than discretized arrays 4. Don’t care if the ODE system is stiff or not.

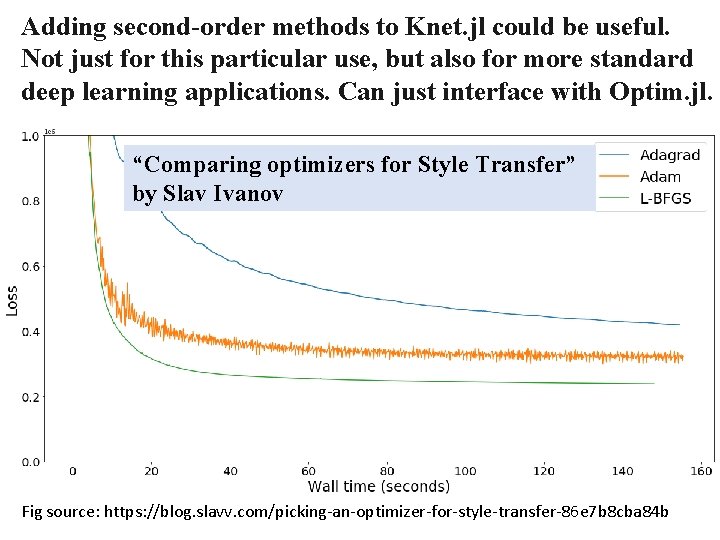
Adding second-order methods to Knet. jl could be useful. Not just for this particular use, but also for more standard deep learning applications. Can just interface with Optim. jl. “Comparing optimizers for Style Transfer” by Slav Ivanov Fig source: https: //blog. slavv. com/picking-an-optimizer-for-style-transfer-86 e 7 b 8 cba 84 b

In most DL frameworks, second-order methods are either missing (e. g. mxnet) or in a huge mess (e. g. Tensor. Flow) (1) Tensorflow’s BFGS method wraps Scipy (tensorflow/contrib/opt/python/training/external_optimizer. py) (2) And Scipy wraps Fortran! (scipy/optimize/lbfgsb/README)

Optim. jl only accepts 1 -D vector. Would be great if it could take arbitrary shapes, otherwise you need to code something like: