Solving Model 7 Presented By Brian Murphy and

Solving Model 7 Presented By: Brian Murphy and Scott Lichtor

Background �Dairy plant produces various flavors of ice creams in 3 gallon containers and distributes them to a chain of ice cream parlors. �Dairy plant knows exact demand from parlors for the next twelve months (January-December). �Plant has huge freezer-warehouse that can store surplus in any one month for sale in future months. �Plant can produce ice cream in regular time or overtime. �Production capabilities vary from month to month due to variations in demand. Question: How many gallons should the dairy plant produce in each month in order to reduce total costs?

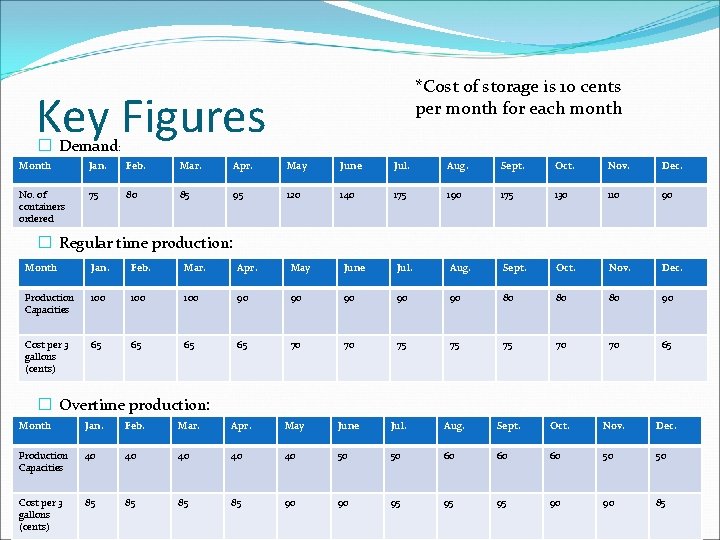
*Cost of storage is 10 cents per month for each month Key Figures � Demand: Month Jan. Feb. Mar. Apr. May June Jul. Aug. Sept. Oct. Nov. Dec. No. of containers ordered 75 80 85 95 120 140 175 190 175 130 110 90 � Regular time production: Month Jan. Feb. Mar. Apr. May June Jul. Aug. Sept. Oct. Nov. Dec. Production Capacities 100 100 90 90 90 80 80 80 90 Cost per 3 gallons (cents) 65 65 70 70 75 75 75 70 70 65 � Overtime production: Month Jan. Feb. Mar. Apr. May June Jul. Aug. Sept. Oct. Nov. Dec. Production Capacities 40 40 40 50 50 60 60 60 50 50 Cost per 3 gallons (cents) 85 85 90 90 95 95 95 90 90 85

Assumptions and Variables Assumptions: �Dairy plant has no finite storage capacity. �Ice cream kept in storage does not go bad or lose value (ice cream produced in January can be sold in December). �All ice cream produced is eventually sold (no leftovers) Variables: �xij = containers produced during regular time in month j for use in month i. �yij = containers produced during overtime in month j for use in month i.

Objective Function �Minimize z = total costs �Broken down into production and storage costs for each month. Regular Production Cost Overtime Production Cost Storage Cost 12 12 12 i=1 i=1 January: 0. 65∑xi, 1 + 0. 85∑yi, 1 + 0. 1∑(i-1)(xi, 1+yi, 1) +February: 0. 65∑xi, 2 + 0. 85∑yi, 2 + 0. 1∑(i-2)(xi, 2+yi, 2) i=2 … +December: . 65 xi, 12 +. 85 yi, 12 i=2

Constraints �Demand Constraints: January: x 1, 1 + y 1, 1 = 75 February: ∑(x 2, j + y 2, j) = 80 12 … j=1 12 December: ∑(x 12, j + y 12, j) = 90 j=1

Constraints (Cont. ) … �Production Constraints: January: ∑xi, 1 ≤ 100, ∑yi, 1 ≤ 40 February: ∑xi, 2 ≤ 100, ∑yi, 2 ≤ 40 12 12 i=1 i=2 December: x 12, 12 ≤ 90, y 12, 12 ≤ 50

Solution �See Excel Sheet