Solving MINLP problems with AIMMS Marcel Hunting Pittsburgh

Solving MINLP problems with AIMMS Marcel Hunting Pittsburgh June 4, 2014 AIMMS Software Developer www. aimms. com

Overview • Introducing AIMMS • Generated Math Program (GMP) • Outer Approximation • AIMMS Presolver • Implement Branch-and-Bound www. aimms. com
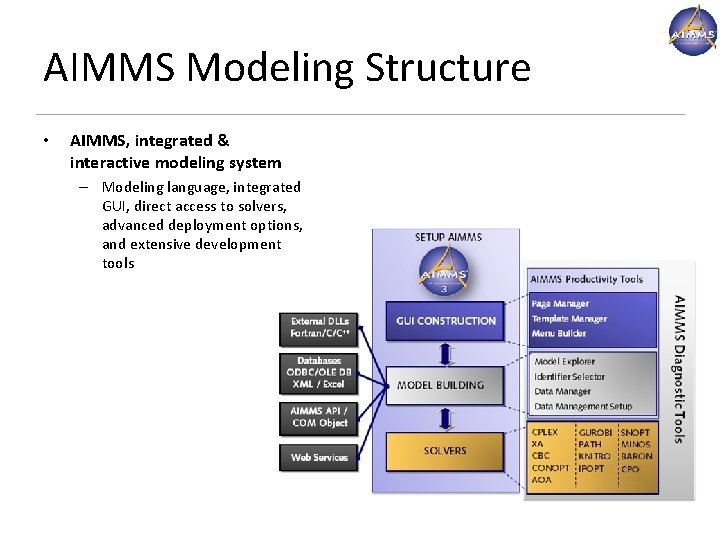
AIMMS Modeling Structure • AIMMS, integrated & interactive modeling system – Modeling language, integrated GUI, direct access to solvers, advanced deployment options, and extensive development tools www. aimms. com
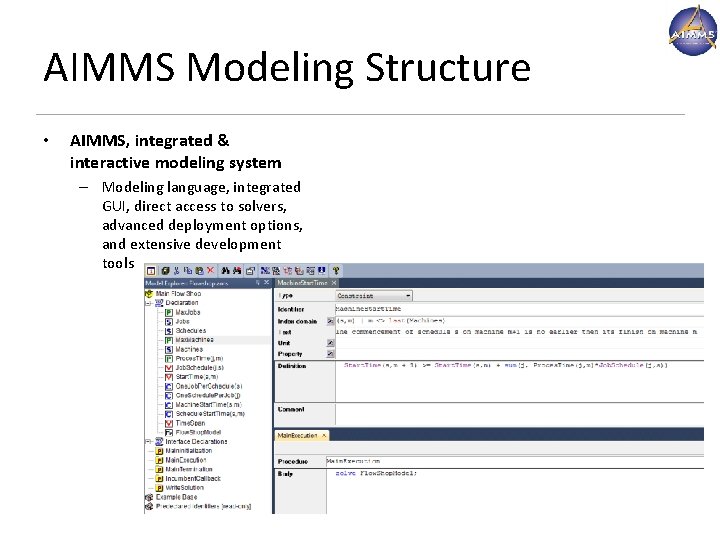
AIMMS Modeling Structure • AIMMS, integrated & interactive modeling system – Modeling language, integrated GUI, direct access to solvers, advanced deployment options, and extensive development tools www. aimms. com
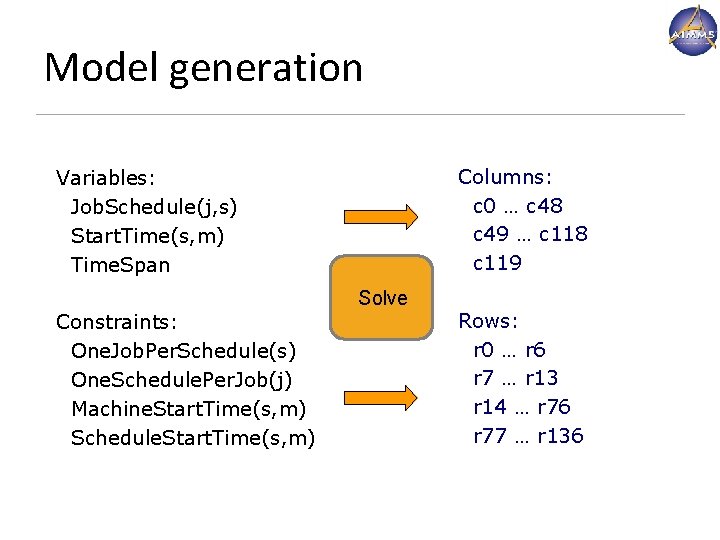
Model generation Columns: c 0 … c 48 c 49 … c 118 c 119 Variables: Job. Schedule(j, s) Start. Time(s, m) Time. Span Solve Constraints: One. Job. Per. Schedule(s) One. Schedule. Per. Job(j) Machine. Start. Time(s, m) Schedule. Start. Time(s, m) Rows: r 0 … r 6 r 7 … r 13 r 14 … r 76 r 77 … r 136 www. aimms. com
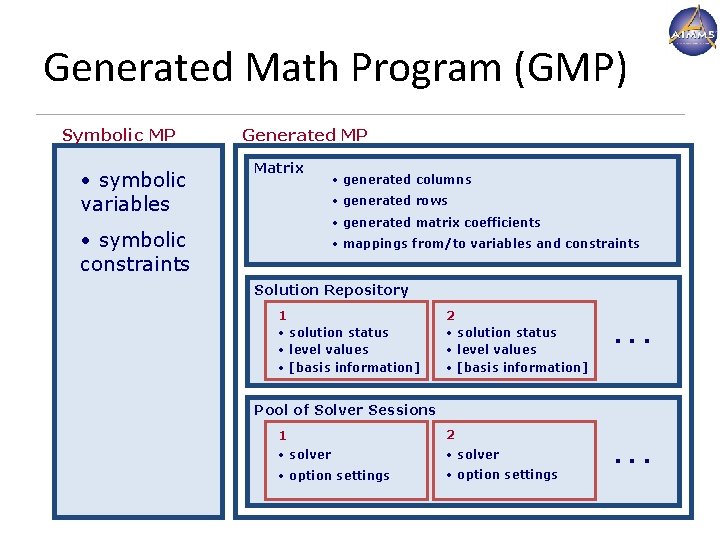
Generated Math Program (GMP) Symbolic MP • symbolic variables Generated MP Matrix • generated columns • generated rows • generated matrix coefficients • symbolic constraints • mappings from/to variables and constraints Solution Repository 1 • solution status • level values • [basis information] 2 • solution status • level values • [basis information] . . . Pool of Solver Sessions 1 2 • solver • option settings . . . www. aimms. com

Basic GMP Normally: solve Math. Program; GMP: my. GMP : = GMP: : Instance: : Generate(Math. Program); GMP: : Instance: : Solve(my. GMP); Modify: GMP: : Column: : Set. Upper. Bound(my. GMP, Start. Time(s 1, m 1), 5); www. aimms. com

Selection of GMP functions • GMP: : Instance: : Generate, Solve, Copy, Fix. Columns, Create. Feasibility. Problem, Create. Presolved • GMP: : Column: : Add, Delete, Freeze, Set. Lower. Bound • GMP: : Row: : Add, Delete, Set. Right. Hand. Side • GMP: : Coefficient: : Set, Get, Set. Quadratic, Get. Quadratic • GMP: : Solution: : Copy, Send. To. Model, Get. Column. Value • GMP: : Linearization: : Add, Delete • GMP: : Solver. Session: : Execute, Asynchronous. Execute www. aimms. com

Outer Approximation module • Module: GMPOuter. Approximation • Call: my. GMP : = GMP: : Instance: : Generate( my. Math. Program ) ; GMPOuter. Approx: : Do. Outer. Approximation( my. GMP ); • Uses AIMMS presolver by default • Can be combined with Multi-start module • Quesada & Grossmann (1992) version for convex MINLP • Uses lazy constraints callback • Uses nested solve www. aimms. com
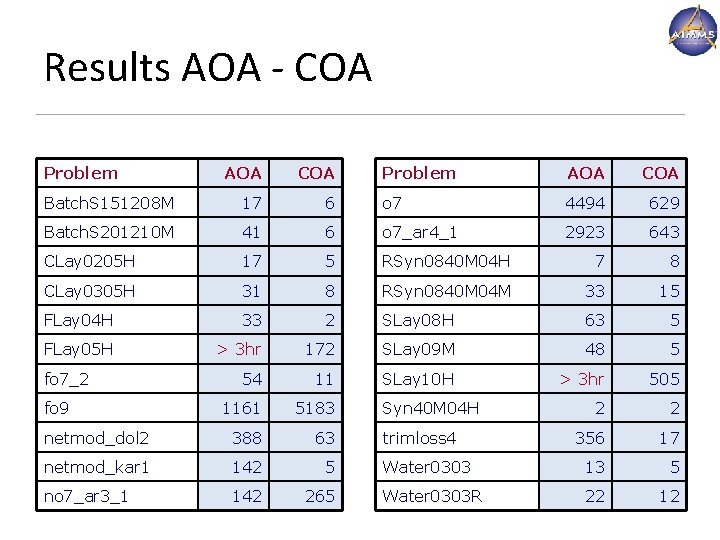
Results AOA - COA Problem AOA COA Batch. S 151208 M 17 6 o 7 4494 629 Batch. S 201210 M 41 6 o 7_ar 4_1 2923 643 CLay 0205 H 17 5 RSyn 0840 M 04 H 7 8 CLay 0305 H 31 8 RSyn 0840 M 04 M 33 15 FLay 04 H 33 2 SLay 08 H 63 5 FLay 05 H > 3 hr 172 SLay 09 M 48 5 54 11 SLay 10 H > 3 hr 505 1161 5183 2 2 netmod_dol 2 388 63 356 17 netmod_kar 1 142 5 Water 0303 13 5 no 7_ar 3_1 142 265 Water 0303 R 22 12 fo 7_2 fo 9 Syn 40 M 04 H trimloss 4 www. aimms. com
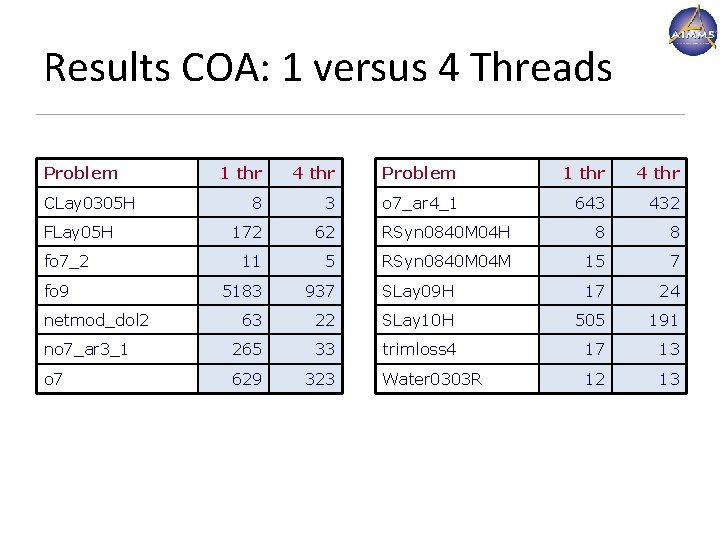
Results COA: 1 versus 4 Threads Problem 1 thr 4 thr 8 3 o 7_ar 4_1 643 432 172 62 RSyn 0840 M 04 H 8 8 11 5 RSyn 0840 M 04 M 15 7 5183 937 SLay 09 H 17 24 63 22 SLay 10 H 505 191 no 7_ar 3_1 265 33 trimloss 4 17 13 o 7 629 323 Water 0303 R 12 13 CLay 0305 H FLay 05 H fo 7_2 fo 9 netmod_dol 2 www. aimms. com

AIMMS Presolver • Delete redundant constraints & fixed variables • Bound Tightening - Feasibility based – Variable x: range [0, inf) -► range [10, 55] – Linear & nonlinear constraints • Improve coefficients (possibly using probing) • Linearize quadratic constraints www. aimms. com

Linearize quadratic constraints • www. aimms. com

Branch-and-Bound MINLP problem with binary variables x(i) and y(i, j). Implement branching; choose most fractional column. gmp. BB: Generated Math Program for a node in B&B tree www. aimms. com

Branching for (i) do x. Lev(i) : = GMP: : Column: : Get. Column. Value( gmp. BB, 1, x(i) ); x. Half. Gap(i) : = abs( x. Lev(i) - 0. 5 ); endfor; x. Most. Fractional. Column : = Arg. Min( i, x. Half. Gap(i) ); for (i, j) do y. Lev(i, j) : = GMP: : Column: : Get. Column. Value( gmp. BB, 1, y(i, j) ); y. Half. Gap(i, j) : = abs( y. Lev(i, j) - 0. 5 ); endfor; y. Most. Fractional. Column : = Arg. Min( (i, j), y. Half. Gap(i, j) ); Most. Fractional. Column : = … www. aimms. com

Branching - Improved Vars : = { ‘x’, ‘y’ }; Col. Nrs : = GMP: : Instance: : Get. Column. Numbers( gmp. BB, Vars ); For example: Col. Nrs = {3, 4, …, 10, 21, …, 43} index: c for (c) do Lev(c) : = GMP: : Column: : Get. Column. Value( gmp. BB, 1, c ); Half. Gap(c) : = abs( Lev(c) - 0. 5 ); endfor; Most. Fractional. Column : = Arg. Min( c, Half. Gap(c) ); www. aimms. com

Branching - Improved Vars : = All. Integer. Variables; Col. Nrs : = GMP: : Instance: : Get. Column. Numbers( gmp. BB, Vars ); For example: Col. Nrs = {3, 4, …, 10, 21, …, 43} index: c for (c) do Lev(c) : = GMP: : Column: : Get. Column. Value( gmp. BB, 1, c ); Half. Gap(c) : = abs( Lev(c) - 0. 5 ); endfor; Most. Fractional. Column : = Arg. Min( c, Half. Gap(c) ); www. aimms. com

www. aimms. com
- Slides: 18