Solving Linear Systems by Linear Combinations Objective Students

Solving Linear Systems by Linear Combinations Objective: • Students will solve a linear system by combinations ( Elimination ).

Algebra Standards: 8. EE. 8 Students solve a system of two linear equations in two variables algebraically, and are able to interpret the answer graphically. Students are able to use this to solve a system of two linear inequalities in two variables, and to sketch the solution sets.

#1 Add the Equations Solve the linear system 2 x + 4 y = 10 { x – 4 y = 20 Solution: 0 2 x + 4 y = 10 x – 4 y = 20 1 1 3 x = 30 3 3 x = 10 Solution is (10, – 5 ) 2 Check answer! x – 4 y = 20 0 10 – 4 y = 20 -10 1 -4 y = 10 -4 -4 y=– 5 2

#2 Add the Equations Solve the linear system 4 x + y = -4 { -4 x + 2 y = 16 Solution: 0 4 x + y = -4 -4 x + 2 y = 16 1 3 y = 12 3 3 y= 4 Solution is (-2, 4) Check answer! -4 x + 2 y = 16 -4 x +2(4) =16 0 -4 x + 8 =16 -8 -8 1 -4 x = 8 -4 -4 x = -2

#3 Multiply then add Solve the linear system x + 5 y = 2 { Check answer! x – 4 y = 20 Solution: x + 5 y = 2 -1[ x – 4 y = 20 ] x + 5 y = 2 x + 5(-2) =2 0 x – 10 = 2 +10 x = 12 0 x + 5 y = 2 -x + 4 y = -20 1 9 y = -18 9 9 y = -2 Solution is (12, -2)

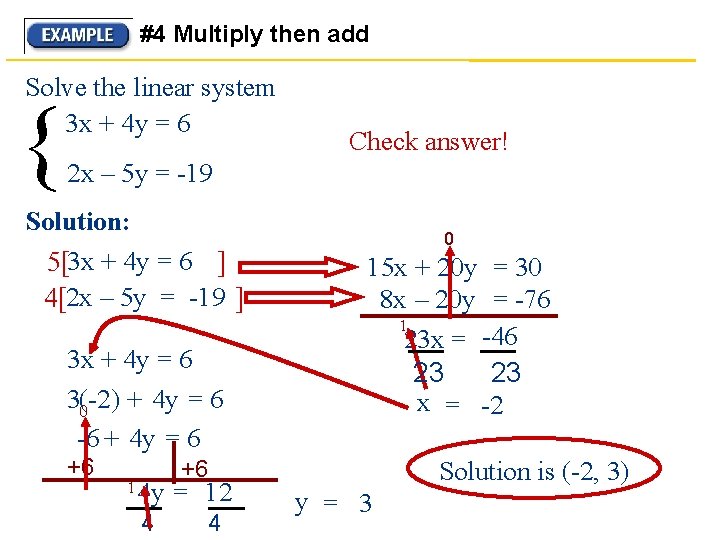
#4 Multiply then add Solve the linear system 3 x + 4 y = 6 { Check answer! 2 x – 5 y = -19 Solution: 5[3 x + 4 y = 6 ] 4[2 x – 5 y = -19 ] 3 x + 4 y = 6 3(-2) + 4 y = 6 0 -6 + 4 y = 6 +6 1 0 15 x + 20 y = 30 8 x – 20 y = -76 1 23 x = -46 23 23 x = -2 +6 4 y = 12 4 4 Solution is (-2, 3) y = 3

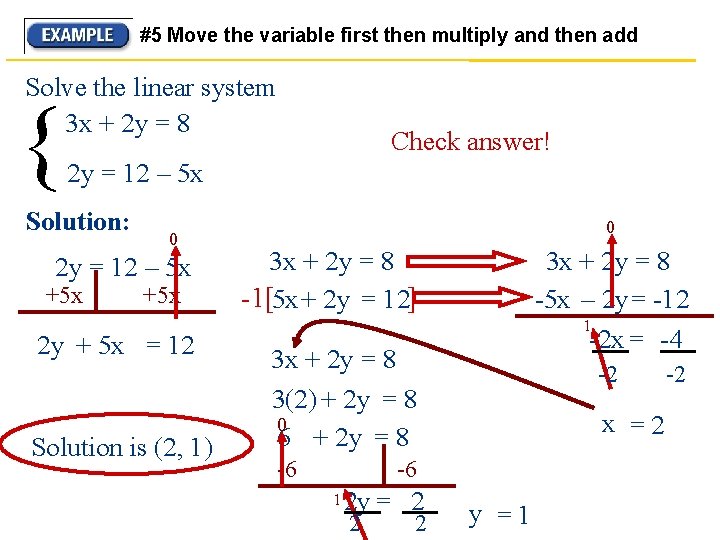
#5 Move the variable first then multiply and then add Solve the linear system 3 x + 2 y = 8 { Check answer! 2 y = 12 – 5 x Solution: 0 2 y = 12 – 5 x +5 x 2 y + 5 x = 12 Solution is (2, 1) 0 3 x + 2 y = 8 -1[5 x+ 2 y = 12] 3 x + 2 y = 8 -5 x – 2 y= -12 1 -2 x = -4 3 x + 2 y = 8 3(2) + 2 y = 8 0 6 + 2 y = 8 -6 -2 x =2 -6 1 2 y = 2 2 2 y =1 -2

#6 Word Problem In one day the National Civil Rights Museum in Memphis, Tennessee, admitted 321 adults and children and collected $1590. The price of admission is $6 for an adult and $4 for a child. How many adults and how many children were admitted to the museum that day? Solution: Money How many x = adults y = children 6 x + 4 y = 1590 x + y = 321 0 -6[x + y = 321 ] 6 x + 4 y = 1590 0 x + 168 = 321 -168 x = 153 -6 x– 6 y = -1926 6 x + 4 y = 1590 – 12 y = -336 -2 -2 153 adults y = 168 children

#7 Word Problem Find two numbers whose sum is 58 and whose difference is 16. Solution: 0 x + y = 58 x – y = 16 1 2 x = 74 2 2 x = 37 x + y = 58 0 37 + y = 58 -37 y = 21 x = 1 st number y = 2 nd number

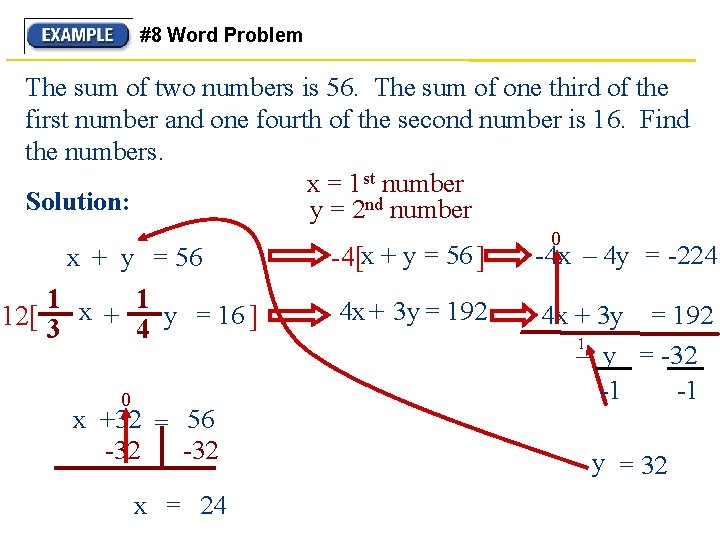
#8 Word Problem The sum of two numbers is 56. The sum of one third of the first number and one fourth of the second number is 16. Find the numbers. x = 1 st number Solution: y = 2 nd number 0 x + y = 56 -4[x + y = 56 ] -4 x – 4 y = -224 1 x 1 + y = 16 ] 12[ 3 4 4 x + 3 y = 192 1 – y = -32 -1 -1 0 x +32 = 56 -32 x = 24 y = 32

#9 Word Problem (Mixture) How many gallons of 30% alcohol solution and how many of 60% alcohol solution must be mixed to produce 18 gallons of 50% solution? Solution: Gallons of Solution x = 30% Alchol Solution(%) y = 60% Alcohol Sol. 10[0. 3 x+ 0. 6 y = (0. 5)18] x + y = 18 18 = 50% Alcohol Sol. 3 x + 6 y = (5)18 0 -3[ x + y = 18 ] -3 x– 3 y = -54 3 x + 6 y = 90 1 3 y = 36 3 3 y = 12 0 x + 12 = 18 -12 x = 6

Assignment Book Pg. 290 # 1, 2, 4, 7, 19