Solving Linear Systems 3 6 in Three Variables

Solving Linear Systems 3 -6 in Three Variables Warm Up Lesson Presentation Lesson Quiz Holt Algebra 22

3 -6 Solving Linear Systems in Three Variables Do Now Solve each system of equations algebraically. 1. x = 4 y + 10 4 x + 2 y = 4 6 x – 5 y = 9 2. 2 x – y =1 Classify each system and determine the number of solutions. 3 x – y = 8 x = 3 y – 1 4. 3. 6 x – 2 y = 2 6 x – 12 y = – 4 Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables Objectives TSW represent solutions to systems of equations in three dimensions graphically. TSW solve systems of equations in three dimensions algebraically. Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables Systems of three equations with three variables are often called 3 -by-3 systems. In general, to find a single solution to any system of equations, you need as many equations as you have variables. Holt Algebra 2

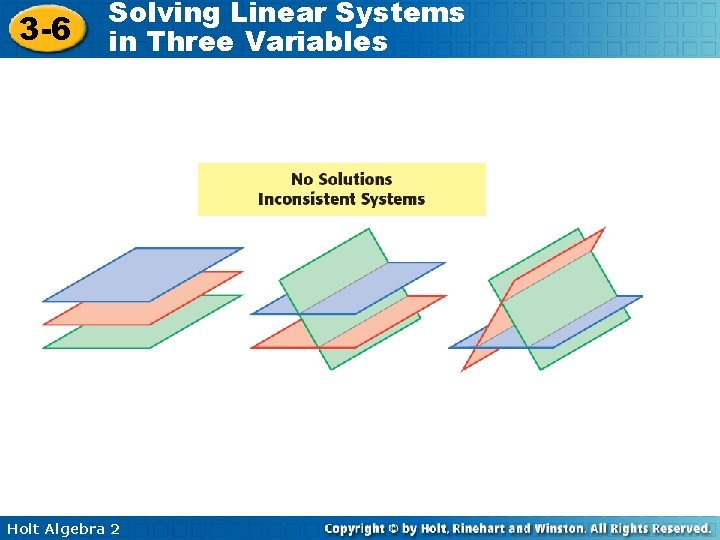
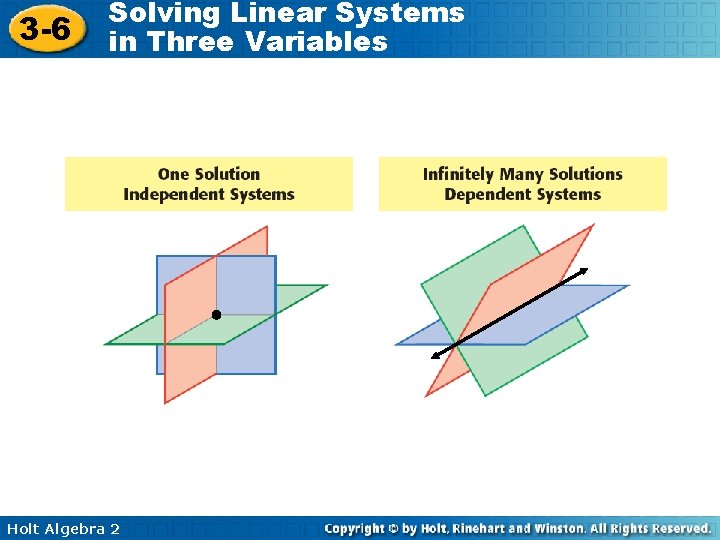
3 -6 Solving Linear Systems in Three Variables When you graph a system of three linear equations in three dimensions, the result is three planes that may or may not intersect. The solution to the system is the set of points where all three planes intersect. These systems may have one, infinitely many, or no solution. Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables • Step One: Eliminate one variable • Step Two: Eliminate another variable and solve for the remaining variable • Step Three: Use one of the equations in you 2 x 2 system to solve for a variable (different than the one previously solved) • Step Four: Substitute the two variables you have solved for into one of the original equations to solve for the remaining variable • Step Five: Write the solution as (x, y, z) Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables Identifying the exact solution from a graph of a 3 -by-3 system can be very difficult. However, you can use the methods of elimination and substitution to reduce a 3 -by-3 system to a 2 -by-2 system and then use the methods that you learned in Lesson 3 -2. Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables Example 1: Solving a Linear System in Three Variables Use elimination to solve the system of equations. 5 x – 2 y – 3 z = – 7 1 2 x – 3 y + z = – 16 2 3 x + 4 y – 2 z = 7 3 Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables Example 1 Continued Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables Example 2 Use elimination to solve the system of equations. –x + y + 2 z = 7 1 2 x + 3 y + z = 1 2 – 3 x – 4 y + z = 4 3 Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables You can also use substitution to solve a 3 -by-3 system. Again, the first step is to reduce the 3 -by-3 system to a 2 -by-2 system. Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables Holt Algebra 2

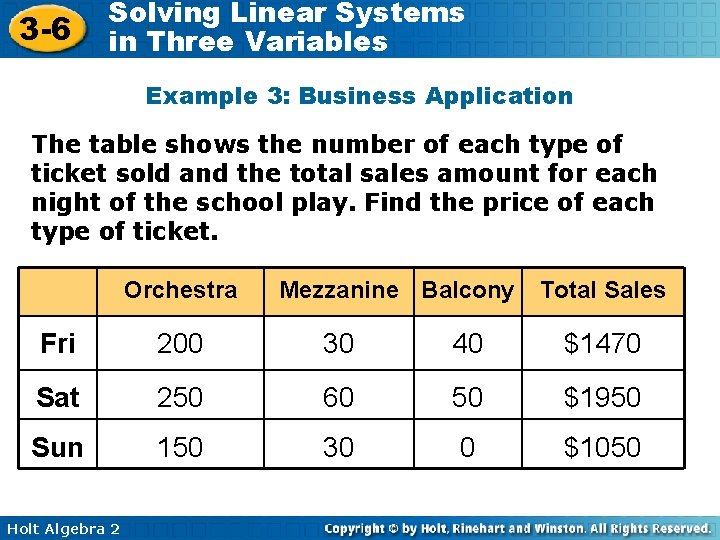
3 -6 Solving Linear Systems in Three Variables Example 3: Business Application The table shows the number of each type of ticket sold and the total sales amount for each night of the school play. Find the price of each type of ticket. Orchestra Mezzanine Balcony Total Sales Fri 200 30 40 $1470 Sat 250 60 50 $1950 Sun 150 30 0 $1050 Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables Holt Algebra 2

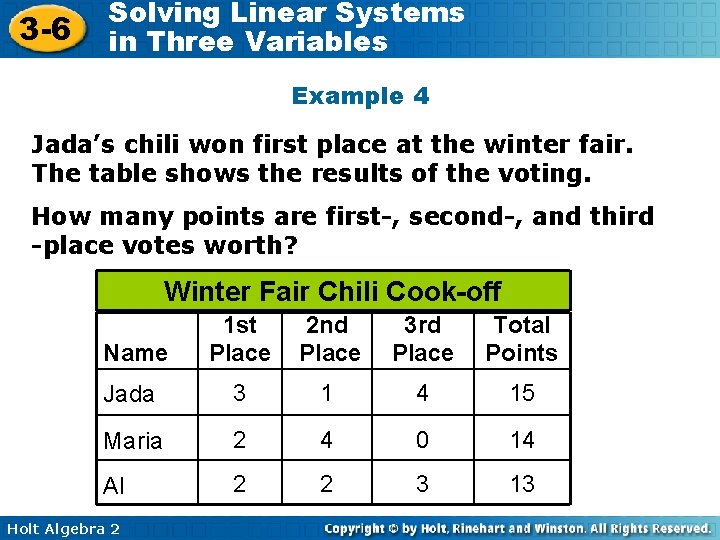
3 -6 Solving Linear Systems in Three Variables Example 4 Jada’s chili won first place at the winter fair. The table shows the results of the voting. How many points are first-, second-, and third -place votes worth? Winter Fair Chili Cook-off Name 1 st Place 2 nd Place 3 rd Place Total Points Jada 3 1 4 15 Maria 2 4 0 14 Al 2 2 3 13 Holt Algebra 2

3 -6 Solving Linear Systems in Three Variables Holt Algebra 2