SOLVING LINEAR PROGRAMMING PROBLEMS The Simplex Method Simplex

SOLVING LINEAR PROGRAMMING PROBLEMS: The Simplex Method

Simplex Method • Used for solving LP problems will be presented • Put into the form of a table, and then a number of mathematical steps are performed on the table • Moves from one extreme point on the solution boundary to another until the best one is found, and then it stops • A lengthy and tedious process but computer software programs are now used easily instead • Programs do not provide an in-depth understanding of how those solutions are derived • Can greatly enhance one's understanding of LP

First Step • First step is to convert model into standard form • s 1 and s 2, represent amount of unused labor and wood • No chairs and tables are produced, s 1=40 and s 2=120 • Unused resources contribute nothing to profit, Z=0 • Decision variables as well as profit at origin are:

Assigning (n-m) Variables Equal to Zero • Determine values of variables at every possible solution point • Have two equations and four unknowns, which makes direct simultaneous solution impossible • Assigns n-m variables=0 – n=number of variables – m=number of constraints • Have n = 4 variables and m = 2 constraints • x 1 = 0 and substituting them results in x 2 = 20 and s 2=60

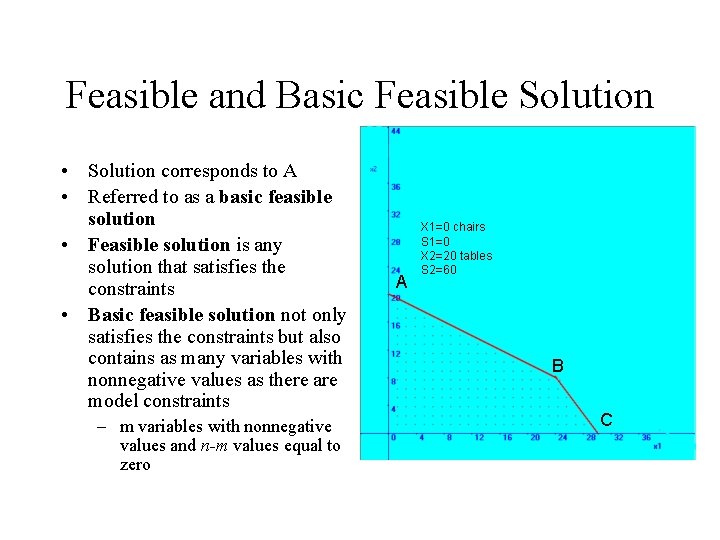
Feasible and Basic Feasible Solution • Solution corresponds to A • Referred to as a basic feasible solution • Feasible solution is any solution that satisfies the constraints • Basic feasible solution not only satisfies the constraints but also contains as many variables with nonnegative values as there are model constraints – m variables with nonnegative values and n-m values equal to zero A X 1=0 chairs S 1=0 X 2=20 tables S 2=60 B C

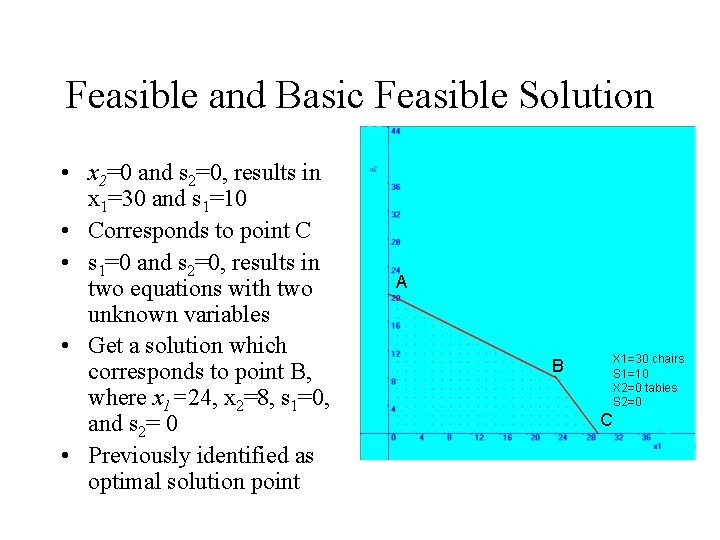
Feasible and Basic Feasible Solution • x 2=0 and s 2=0, results in x 1=30 and s 1=10 • Corresponds to point C • s 1=0 and s 2=0, results in two equations with two unknown variables • Get a solution which corresponds to point B, where x 1=24, x 2=8, s 1=0, and s 2= 0 • Previously identified as optimal solution point A X 1=30 chairs S 1=10 X 2=0 tables S 2=0 B C

Two Questions • Two questions can be raised by the identification of solutions at points O, A, B, and C • How was it known which variables to set equal to zero? • How is the optimal solution identified? • Answers these questions by performing a set of mathematical steps • Determines at each step which variables should equal zero and when an optimal solution has been reached A X 1=0 chairs S 1=0 X 2=20 tables S 2=60 X 1=24 chairs S 1=0 X 2=8 tables S 2=0 B C X 1=30 chairs S 1=10 X 2=0 tables S 2=0

Initial Tableau • Model is put into the form of a table, or tableau • Our maximization model • Z = 40 x 1 + 50 x 2 + 0 s 1 + 0 s 2 Subject to x 1 + 2 x 2+ s 1 = 40 4 x 1 + 3 x 2 + s 2 =120 x 1, x 2 , s 1, s 2 ≥ 0 • • Initial simplex tableau with various column and row headings Record the model decision variables, followed by the slack variables Bottom rows represent constraint equations whose right-hand sides are given in the “solution” column z-row is obtained from z -40 x 1 -50 x 2=0 Basic Z x 1 x 2 s 1 s 2 Solution Z 1 -40 -50 0 s 1 0 1 2 1 0 40 s 2 0 4 3 0 1 120

Determining Basic Feasible Solution • Determine a basic feasible solution • Know which two variables will form the basic feasible solution and which will be assigned a value of zero? • Selects the origin as the initial basic feasible solution • x 1= 0 and x 2= 0; variables in basic feasible solution are s 1 and s 2 which are listed under column "Basic" and their values, 40 and 120, are listed under column “solution“ • Z=0 under column “solution” Basic Z x 1 x 2 s 1 s 2 Solution Z 1 -40 -50 0 s 1 0 1 2 1 0 40 s 2 0 4 3 0 1 120

Entering Variable • • • Interested in giving us either some chairs or some tables Want nonbasic variables will enter solution and become basic z-row values represent increase per unit of entering a nonbasic variable into the basic solution Make as much money as possible Select variable x 2 as the entering basic variable – has the greatest increase in profit per unit, $50—the most negative value in the z-row • • x 2 column is highlighted and is referred to as the pivot column Referred to in mathematical terminology as pivot operations Basic Z x 1 x 2 s 1 s 2 Solution Z 1 -40 -50 0 s 1 0 1 2 1 0 40 s 2 0 4 3 0 1 120

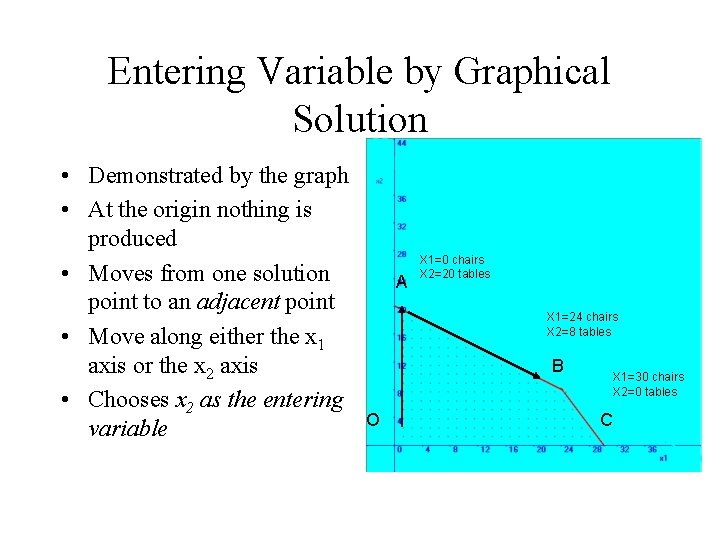
Entering Variable by Graphical Solution • Demonstrated by the graph • At the origin nothing is produced • Moves from one solution point to an adjacent point • Move along either the x 1 axis or the x 2 axis • Chooses x 2 as the entering variable A X 1=0 chairs X 2=20 tables X 1=24 chairs X 2=8 tables B O X 1=30 chairs X 2=0 tables C

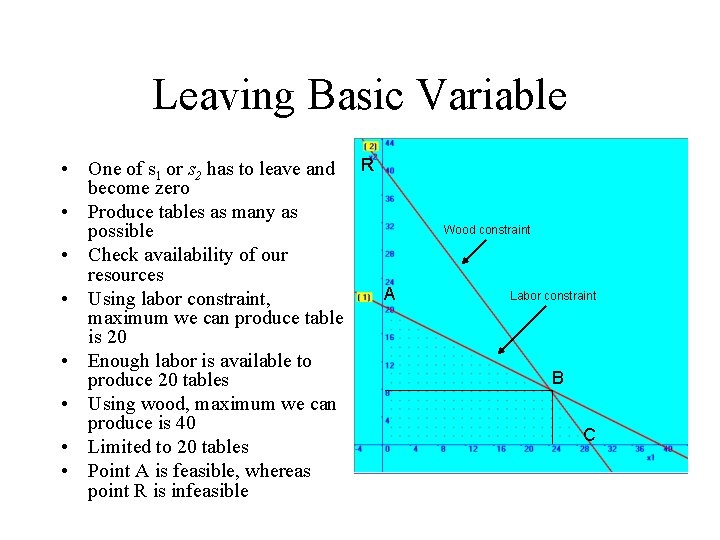
Leaving Basic Variable • One of s 1 or s 2 has to leave and R become zero • Produce tables as many as possible • Check availability of our resources A • Using labor constraint, maximum we can produce table is 20 • Enough labor is available to produce 20 tables • Using wood, maximum we can produce is 40 • Limited to 20 tables • Point A is feasible, whereas point R is infeasible Wood constraint Labor constraint B C

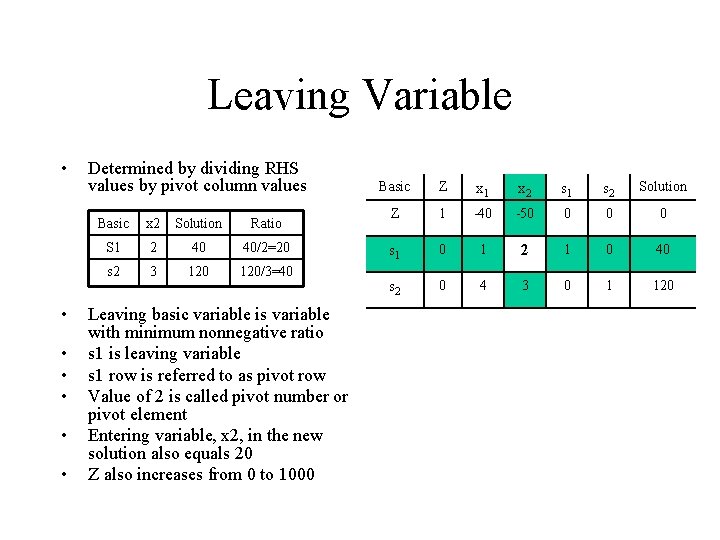
Leaving Variable • • Determined by dividing RHS values by pivot column values Basic x 2 Solution Ratio S 1 2 40 40/2=20 s 2 3 120/3=40 Leaving basic variable is variable with minimum nonnegative ratio s 1 is leaving variable s 1 row is referred to as pivot row Value of 2 is called pivot number or pivot element Entering variable, x 2, in the new solution also equals 20 Z also increases from 0 to 1000 Basic Z x 1 x 2 s 1 s 2 Solution Z 1 -40 -50 0 s 1 0 1 2 1 0 40 s 2 0 4 3 0 1 120

Second Tableau • Nonbasic and basic variables at solution point Nonbasic: x 1 and s 1 Basic: x 2 and s 2 • Various values are computed using pivot row and all other rows • First, x 2 row, is computed by using every value in pivot row of first (old) tableau and divide it by pivot number, or (0/2 1/2 2/2 1/2 0/2 40/2) • New row values are shown in Table Basic Z x 1 x 2 s 1 s 2 Solution Z 1 -40 -50 0 x 2 0 1/2 1 1/2 0 20 s 2 0 4 3 0 1 120

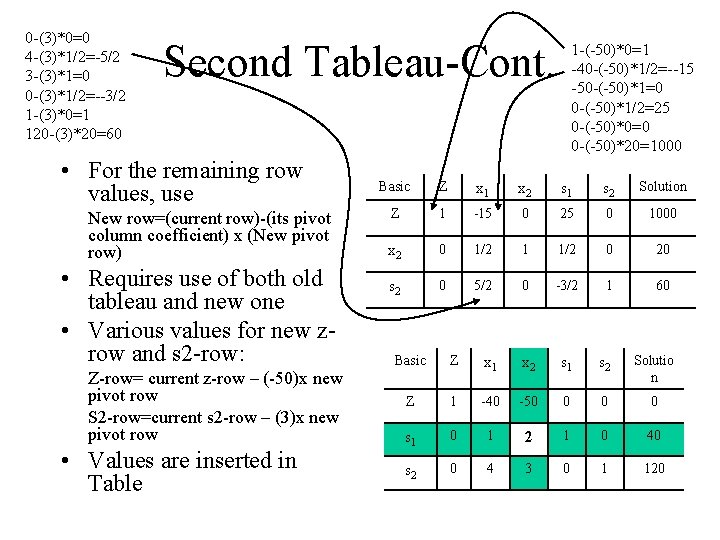
0 -(3)*0=0 4 -(3)*1/2=-5/2 3 -(3)*1=0 0 -(3)*1/2=--3/2 1 -(3)*0=1 120 -(3)*20=60 Second Tableau-Cont. • For the remaining row values, use New row=(current row)-(its pivot column coefficient) x (New pivot row) • Requires use of both old tableau and new one • Various values for new zrow and s 2 -row: Z-row= current z-row – (-50)x new pivot row S 2 -row=current s 2 -row – (3)x new pivot row • Values are inserted in Table 1 -(-50)*0=1 -40 -(-50)*1/2=--15 -50 -(-50)*1=0 0 -(-50)*1/2=25 0 -(-50)*0=0 0 -(-50)*20=1000 Basic Z x 1 x 2 s 1 s 2 Solution Z 1 -15 0 25 0 1000 x 2 0 1/2 1 1/2 0 20 s 2 0 5/2 0 -3/2 1 60 Basic Z x 1 x 2 s 1 s 2 Solutio n Z 1 -40 -50 0 s 1 0 1 2 1 0 40 s 2 0 4 3 0 1 120

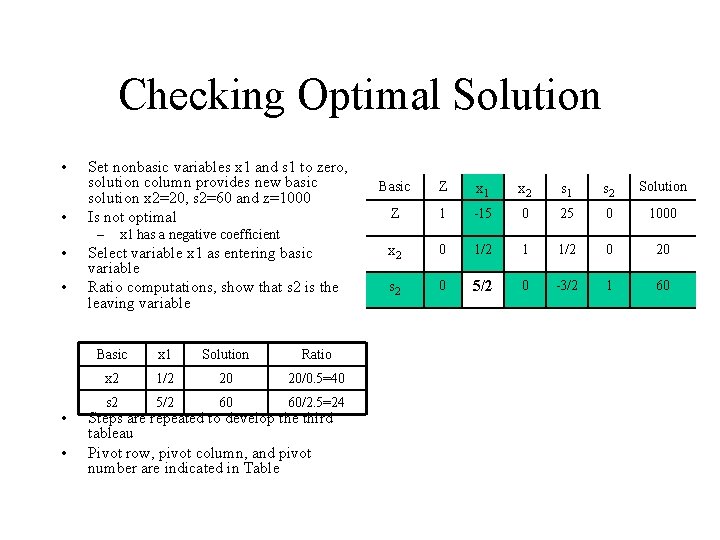
Checking Optimal Solution • • Set nonbasic variables x 1 and s 1 to zero, solution column provides new basic solution x 2=20, s 2=60 and z=1000 Is not optimal – • • x 1 has a negative coefficient Select variable x 1 as entering basic variable Ratio computations, show that s 2 is the leaving variable Basic x 1 Solution Ratio x 2 1/2 20 20/0. 5=40 s 2 5/2 60 60/2. 5=24 Steps are repeated to develop the third tableau Pivot row, pivot column, and pivot number are indicated in Table Basic Z x 1 x 2 s 1 s 2 Solution Z 1 -15 0 25 0 1000 x 2 0 1/2 1 1/2 0 20 s 2 0 5/2 0 -3/2 1 60

Third Tableau • New pivot row, x 1, is computed using the same formula • All old pivot row values are divided by 5/2 • Values for z-row and s 2 -row are computed here and shown in Table Basic Z x 1 x 2 s 1 s 2 Solution Z 1 0 0 16 6 1360 x 2 0 0 1 4/5 -1/5 8 x 1 0 -3/5 24 Basic Z x 1 x 2 s 1 s 2 Solutio n Z 1 -15 0 25 0 1000 x 2 0 1/2 1 1/2 0 20 s 2 0 5/2 0 -3/2 1 60

Checking Optimal Solution • Coefficient of nonbasic variables are positive • Optimal solution has been reached • x 1 = 24 chairs, x 2= 8 tables and z= $1, 360 profit – Corresponds to point B shown previously Basic Z x 1 x 2 s 1 s 2 Solution Z 1 0 0 16 6 1360 x 2 0 0 1 4/5 -1/5 8 x 1 0 -3/5 24

Summary of the Simplex 1. Transform constraint inequalities into equations 2. Set up the initial tableau 3. Determine the pivot column (entering nonbasic solution variable) 4. Determine the pivot row (leaving basic solution variable) 5. Compute the new pivot row values 6. Compute all other row values 7. Determine whether or not the new solution is optimal 1. If these coefficients are zero or positive, the solution is optimal 2. If a negative value exists, return to step 3 and repeat the simplex steps

Simplex Tableaus by TORA • Used manually to solve relatively small problems • Can be so time-consuming and subject to error that manual computation • Computer solution has become so important • Many computer programs use the simplex method • Computer output includes option to display simplex tableaus • Simplex tableaus provided by TORA software

Minimization Problem • Demonstrated simplex method for a maximization problem • A minimization problem requires a few changes • Recall the minimization model minimize Z = 6 x 1 + 3 x 2 subject to 2 x 1 + 4 x 2 ≥ 16 4 x 1 + 3 x 2 ≥ 24 x 1 and x 2 ≥ 0 • Transformed this model into standard form by subtracting surplus variables 2 x 1 + 4 x 2 – s 1 = 16 4 x 1 + 3 x 2 – s 2 = 24

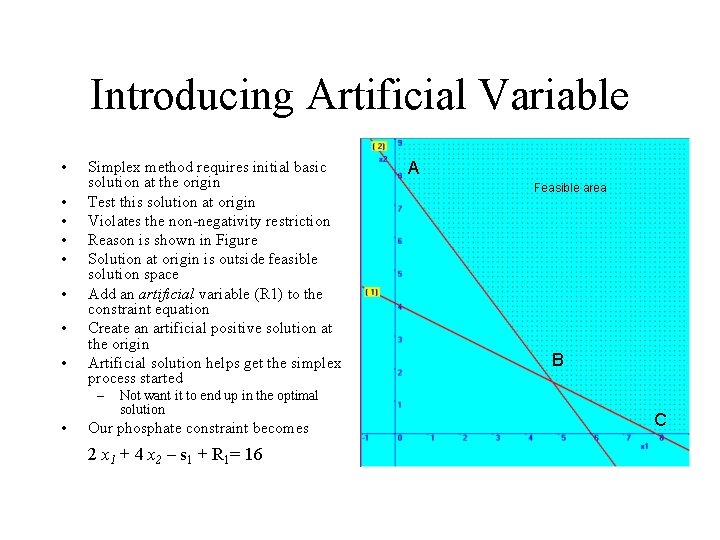
Introducing Artificial Variable • • Simplex method requires initial basic solution at the origin Test this solution at origin Violates the non-negativity restriction Reason is shown in Figure Solution at origin is outside feasible solution space Add an artificial variable (R 1) to the constraint equation Create an artificial positive solution at the origin Artificial solution helps get the simplex process started – • Not want it to end up in the optimal solution Our phosphate constraint becomes 2 x 1 + 4 x 2 – s 1 + R 1= 16 A Feasible area B C

Effect of Surplus and Artificial Variables on Objective Function • • Effect of surplus and artificial variables on objective function Surplus variable has no effect on objective function 0 is assigned to each surplus variable Must also ensure that an artificial variable is not in the final solution Achieved by assigning a very large cost Assign a value of M, which represents a large positive cost Produces objective function: Minimization model can now be summarized as minimize Z = 6 x 1 + 3 x 2 + MR 1 + MR 2 subject to 2 x 1 + 4 x 2 – s 1 + R 1 = 16 4 x 1 + 3 x 2 – s 2 + R 2 = 24 x 1, x 2, s 1, s 2 , R 1, R 2 ≥ 0.

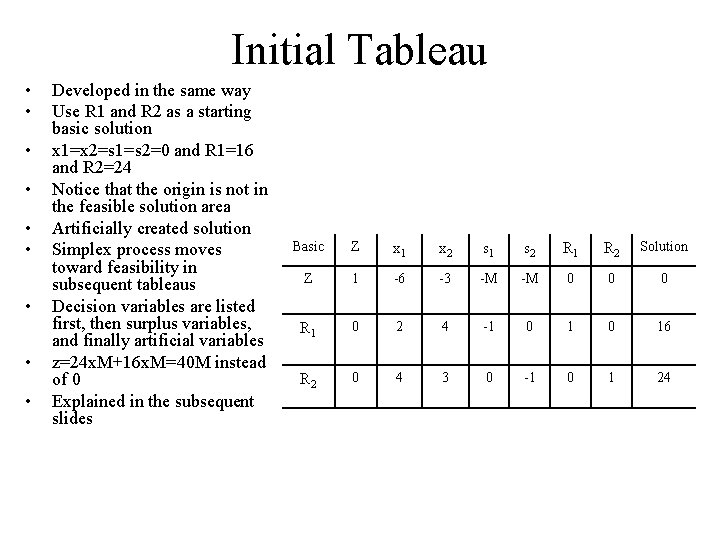
Initial Tableau • • • Developed in the same way Use R 1 and R 2 as a starting basic solution x 1=x 2=s 1=s 2=0 and R 1=16 and R 2=24 Notice that the origin is not in the feasible solution area Artificially created solution Simplex process moves toward feasibility in subsequent tableaus Decision variables are listed first, then surplus variables, and finally artificial variables z=24 x. M+16 x. M=40 M instead of 0 Explained in the subsequent slides Basic Z x 1 x 2 s 1 s 2 R 1 R 2 Solution Z 1 -6 -3 -M -M 0 0 0 R 1 0 2 4 -1 0 16 R 2 0 4 3 0 -1 0 1 24

Modification in Initial Tableau • Inconsistency exists because R 1 and R 2 coefficient have nonzero coefficient • Eliminate this inconsistency by substituting out R 1 and R 2 in the z-row • We can write R 1 =16 -2 x 1 -4 x 2 +s 1 R 2 = 24 -4 x 1 -3 x 2 + s 2 • Substituting R 1 and R 2 in objective function Z = 6 x 1 + 3 x 2 + M (16 -2 x 1 -4 x 2 +s 1 )+ M(24 -4 x 1 -3 x 2 + s 2 ) Z = 40 M+x 1 ( 6 -6 M)+x 2 (3 -7 M) +Ms 1+ Ms 2 • Transforming objective function into standard form Z +x 1 ( -6+6 M)+x 2 (-3+7 M)-Ms 1 - Ms 2= 40 M • Must be used as the z-row

Entering and Leaving Variables • Modified tableau thus becomes • z=40 M, which is consistent now with values of the starting basic feasible solution R 1=24 and R 2=16 • x 2 column is selected as the entering variable because 7 M - 3 is the largest value in z-row • R 1 is selected as leaving basic variable because the ratio of 4 • Second tableau is developed using simplex formulas Basic Z x 1 x 2 s 1 s 2 R 1 R 2 Solution Z 1 6 M-6 7 M-3 -M -M 0 0 40 M R 1 0 2 4 -1 0 16 R 2 0 4 3 0 -1 0 1 24

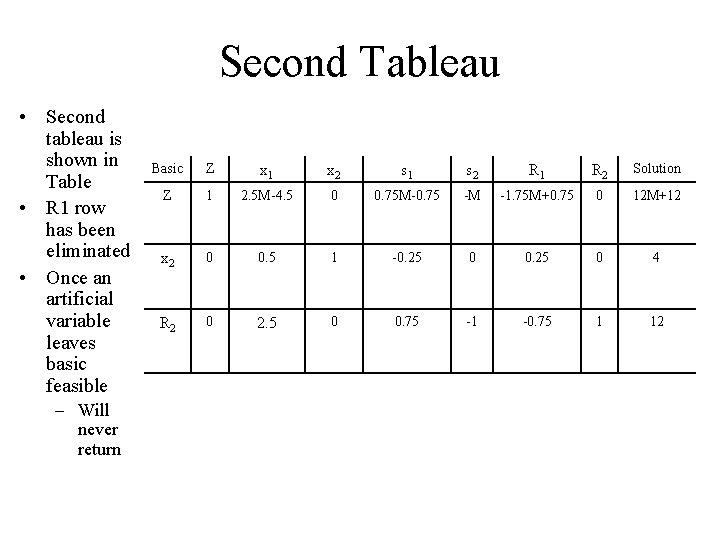
Second Tableau • Second tableau is shown in Table • R 1 row has been eliminated • Once an artificial variable leaves basic feasible – Will never return Basic Z x 1 x 2 s 1 s 2 R 1 R 2 Solution Z 1 2. 5 M-4. 5 0 0. 75 M-0. 75 -M -1. 75 M+0. 75 0 12 M+12 x 2 0 0. 5 1 -0. 25 0 4 R 2 0 2. 5 0 0. 75 -1 -0. 75 1 12

Third Tableau • Third tableau starts replacing R 2 with x 1 • R 1 and R 2 rows have been now eliminated • x 1 row was selected as the pivot row • -4 value for the x 2 row was not considered

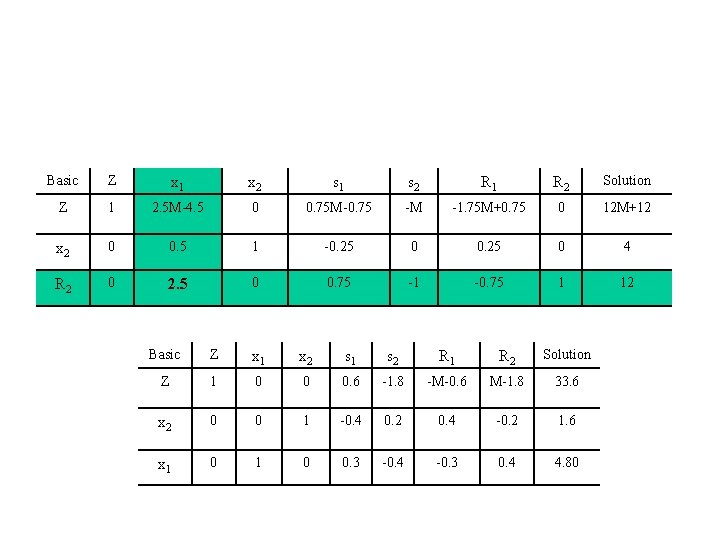
Basic Z x 1 x 2 s 1 s 2 R 1 R 2 Solution Z 1 2. 5 M-4. 5 0 0. 75 M-0. 75 -M -1. 75 M+0. 75 0 12 M+12 x 2 0 0. 5 1 -0. 25 0 4 R 2 0 2. 5 0 0. 75 -1 -0. 75 1 12 Basic Z x 1 x 2 s 1 s 2 R 1 R 2 Solution Z 1 0 0 0. 6 -1. 8 -M-0. 6 M-1. 8 33. 6 x 2 0 0 1 -0. 4 0. 2 0. 4 -0. 2 1. 6 x 1 0 0. 3 -0. 4 -0. 3 0. 4 4. 80

Forth Tableau (Optimal Solution) • Starts replacing s 1 with x 1 • Turns out into final tableau which gives optimal solution – z-row contains no positive values • Optimal solution: • x 1=0, s 1=16, x 2=8, s 2= 0, and Z = $24

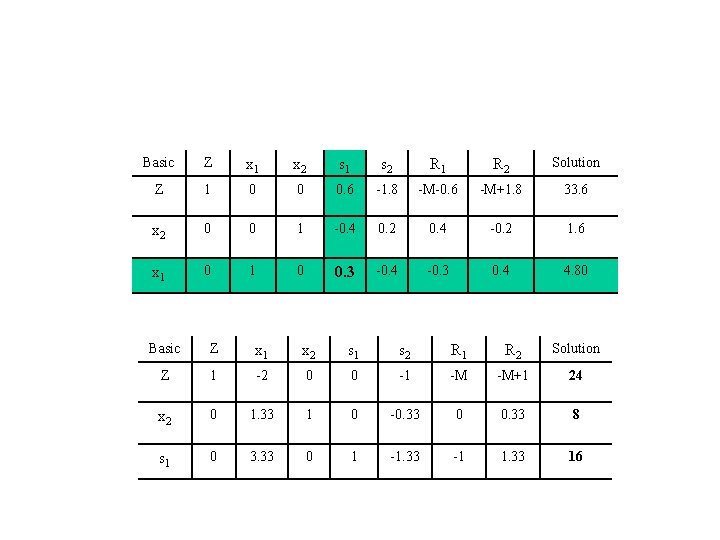
Basic Z x 1 x 2 s 1 s 2 R 1 R 2 Solution Z 1 0 0 0. 6 -1. 8 -M-0. 6 -M+1. 8 33. 6 x 2 0 0 1 -0. 4 0. 2 0. 4 -0. 2 1. 6 x 1 0 0. 3 -0. 4 -0. 3 0. 4 4. 80 Basic Z x 1 x 2 s 1 s 2 R 1 R 2 Solution Z 1 -2 0 0 -1 -M -M+1 24 x 2 0 1. 33 1 0 -0. 33 0 0. 33 8 s 1 0 3. 33 0 1 -1. 33 -1 1. 33 16

Mixed Constraints LP Problems • Discussed maximization problems with all “≥” constraints and minimization problems with all “≤” constraints • Solve a problem with a mixture of “≤”, “≥”, and “=“ constraints • A maximization problem with “≤”, “≥”, and “=“ constraints Max z=$400 x 1+200 x 2 Subject to x 1+x 2=30 2 x 1+8 x 2≥ 80 x 1≤ 20 x 1, x 2≥ 0

First Step • Transform the inequalities into equations • First constraint is an equation – Not necessary to add a slack variable • • • Test it at the origin Constraint is not feasible in this form “≥” constraint did not work at origin either Same thing can be done here At the origin, x 1=0 and x 2=0, 0 + R 1= 30; R 1=30 Artificial variable cannot be assigned a positive value of M in objective function A positive M value would definitely end up in final solution Must give artificial variable a large negative value, or —M Other constraints are transformed into equations Completely transformed LP problem Max z=$400 x 1+200 x 2 -MR 1 -MR 2 s. t. x 1+x 2+R 1=30 2 x 1+8 x 2 -s 1+R 2=80 x 1+s 2=20

Initial Tableau • Initial tableau is shown in Table • Basic solution variables are a mix of artificial and slack variables • Second, third, and optimal tableaus are shown in following slides

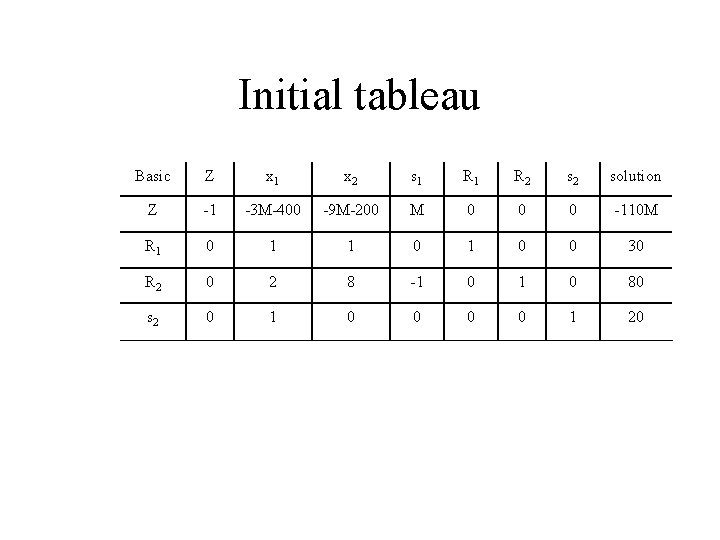
Initial tableau Basic Z x 1 x 2 s 1 R 2 solution Z -1 -3 M-400 -9 M-200 M 0 0 0 -110 M R 1 0 1 0 0 30 R 2 0 2 8 -1 0 80 s 2 0 1 0 0 1 20

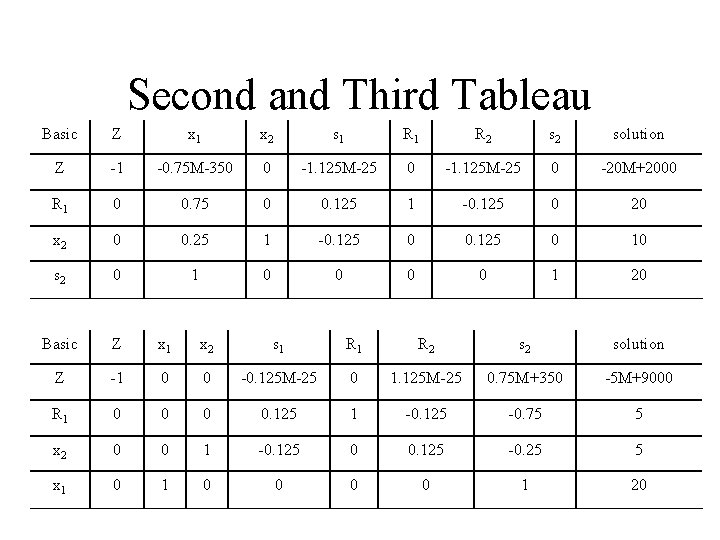
Second and Third Tableau Basic Z x 1 x 2 s 1 R 2 solution Z -1 -0. 75 M-350 0 -1. 125 M-25 0 -20 M+2000 R 1 0 0. 75 0 0. 125 1 -0. 125 0 20 x 2 0 0. 25 1 -0. 125 0 10 s 2 0 1 0 0 1 20 Basic Z x 1 x 2 s 1 R 2 solution Z -1 0 0 -0. 125 M-25 0 1. 125 M-25 0. 75 M+350 -5 M+9000 R 1 0 0. 125 1 -0. 125 -0. 75 5 x 2 0 0 1 -0. 125 0 0. 125 -0. 25 5 x 1 0 0 0 0 1 20

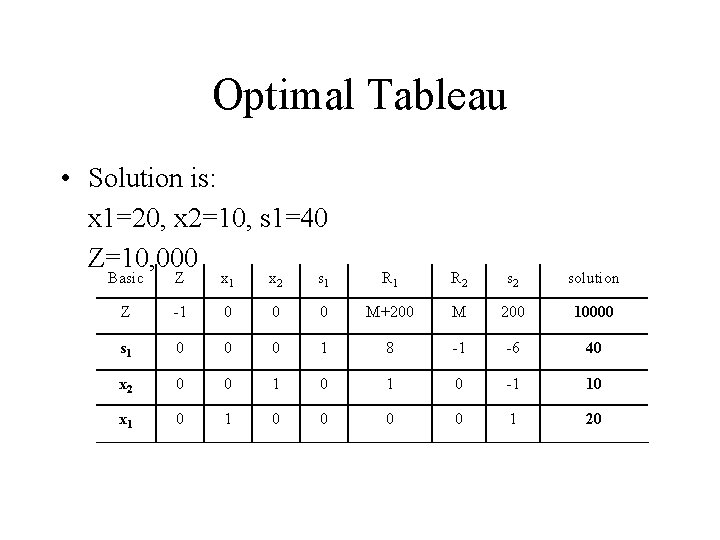
Optimal Tableau • Solution is: x 1=20, x 2=10, s 1=40 Z=10, 000 Basic Z x 1 x 2 s 1 R 2 solution Z -1 0 0 0 M+200 M 200 10000 s 1 0 0 0 1 8 -1 -6 40 x 2 0 0 1 0 -1 10 x 1 0 0 0 0 1 20

Transforming Rules • Rules for transforming all three types of model constraints • Are as follows Objective Function Coefficient Constraint Adjustment Max Min ≤ Add a slack variable 0 0 = Add an artificial variable -M M ≥ Subtract a surplus variable add an artificial variable 0 -M 0 M

Simplex Method of the • • Steps: Starts at origin, point A Moves to an adjacent corner point, either B or F Because of higher coefficient of x 1, it moves toward corner point B At B, the process is repeated for higher z value Finds point C (the final one) Three iterations A B C E nd 2 Example D F A Max z=3 x 1+2 x 2 s. t. x 1 +2 x 2 6 2 x 1+x 2 8 -x 1+x 2 1 x 2 2 x 1, x 2 0 C B

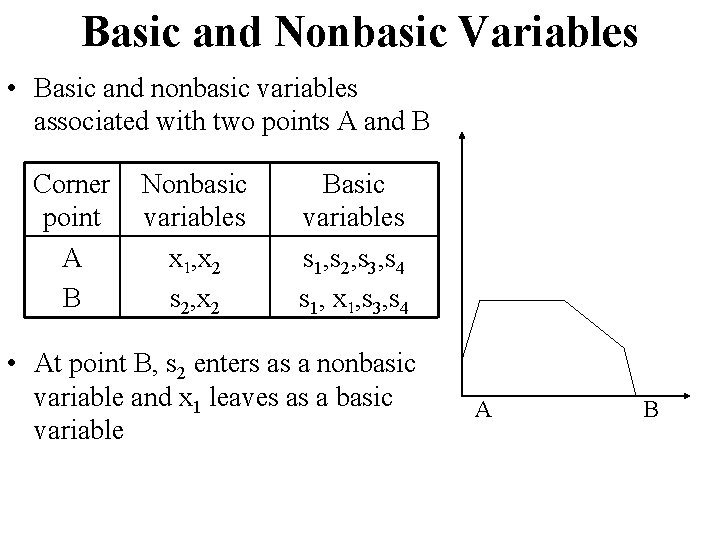
Basic and Nonbasic Variables • Basic and nonbasic variables associated with two points A and B Corner point A B Nonbasic variables x 1, x 2 s 2, x 2 Basic variables s 1, s 2, s 3, s 4 s 1, x 1, s 3, s 4 • At point B, s 2 enters as a nonbasic variable and x 1 leaves as a basic variable A B

The Standard Form and the General Concept • m equations (m=4) • n unknowns (n=6) • Sets (n-m) variables to zero and then solves for the remaining m unknowns • The variables set equal to zero are called nonbasic variables. The remaining ones are called basic variables • At point A, x 1 =x 2=0 which yields s 1 =6, s 2 =8, s 3=1, and s 4=2 • At point B, s 2 =x 2=0, which yields x 1 =4, s 1 =2, s 3=5, and s 4=2 Max z=3 x 1 +2 x 2+0 s 1 +0 s 2 +0 s 3 +0 s 4 s. t. x 1 +2 x 2+s 1 =6 2 x 1 +x 2 +s 2 =8 -x 1 +x 2 +s 3 =1 x 2 +s 4=2 x 1, x 2, s 1, s 2, s 3, s 4 0 A B

The Simplex Method in Tabular Form z-3 x 1 -2 x 2+0 s 1 +0 s 2 +0 s 3 +0 s 4 =0 Obj fcn x 1 +2 x 2+s 1 =6 2 x 1 +x 2 +s 2 =8 Constraint -x 1 +x 2 +s 3 =1 Equations x 2 +s 4 =2

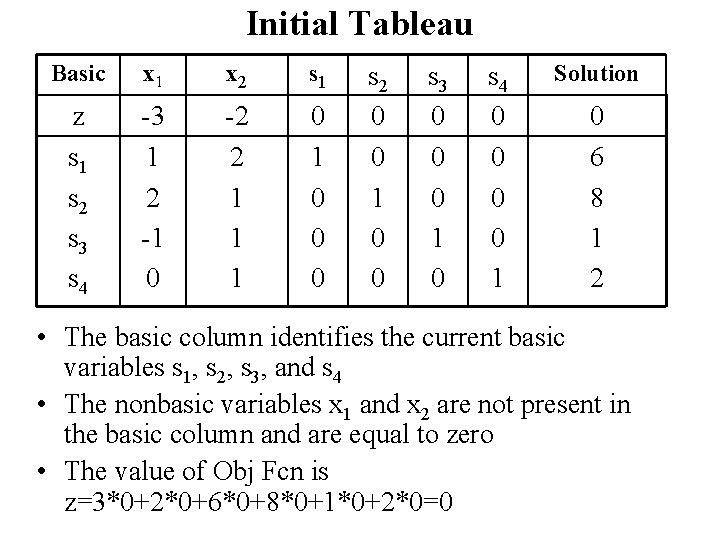
Initial Tableau Basic x 1 x 2 s 1 z s 1 s 2 s 3 s 4 -3 1 2 -1 0 -2 2 1 1 1 0 0 0 s 2 0 0 1 0 0 s 3 0 0 0 1 0 s 4 0 0 1 Solution 0 6 8 1 2 • The basic column identifies the current basic variables s 1, s 2, s 3, and s 4 • The nonbasic variables x 1 and x 2 are not present in the basic column and are equal to zero • The value of Obj Fcn is z=3*0+2*0+6*0+8*0+1*0+2*0=0

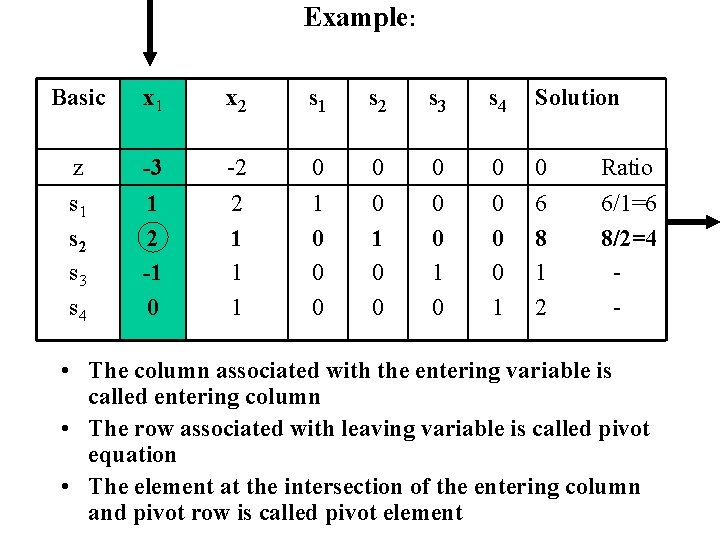
Example: Basic x 1 x 2 s 1 s 2 s 3 s 4 Solution z -3 -2 0 0 0 Ratio s 1 s 2 s 3 s 4 1 2 -1 0 2 1 1 0 0 0 0 1 6 8 1 2 6/1=6 8/2=4 - • The column associated with the entering variable is called entering column • The row associated with leaving variable is called pivot equation • The element at the intersection of the entering column and pivot row is called pivot element

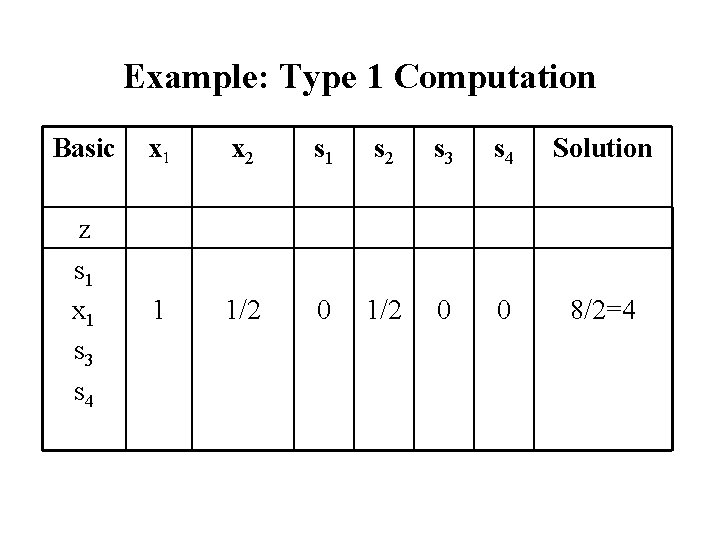
Example: Type 1 Computation Basic x 1 x 2 s 1 s 2 s 3 s 4 Solution z s 1 x 1 s 3 s 4 1 1/2 0 0 8/2=4

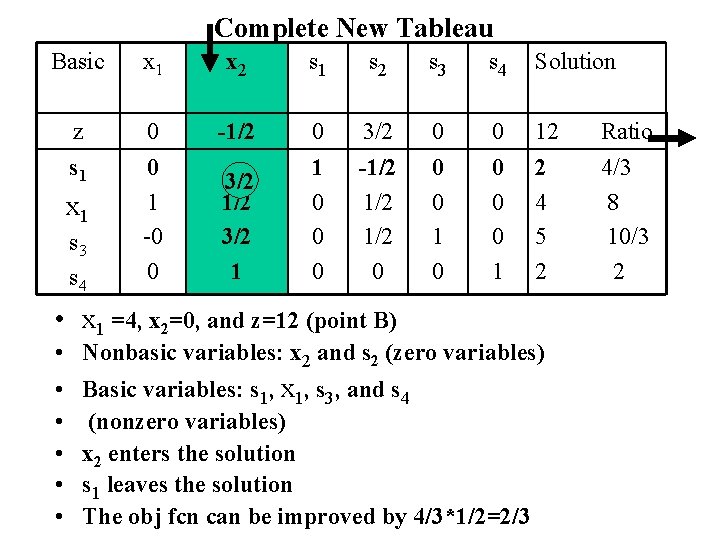
Complete New Tableau Basic x 1 x 2 s 1 s 2 s 3 s 4 Solution z 0 -1/2 0 3/2 0 0 12 Ratio s 1 0 1 -0 0 3/2 1/2 3/2 1 1 0 0 0 -1/2 1/2 0 0 0 1 2 4 5 2 4/3 8 10/3 2 x 1 s 3 s 4 • x 1 =4, x 2=0, and z=12 (point B) • • • Nonbasic variables: x 2 and s 2 (zero variables) Basic variables: s 1, x 1, s 3, and s 4 (nonzero variables) x 2 enters the solution s 1 leaves the solution The obj fcn can be improved by 4/3*1/2=2/3

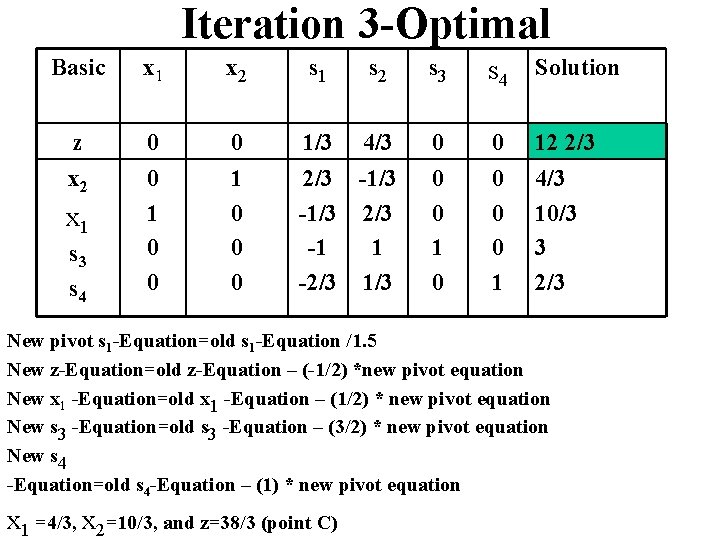
Iteration 3 -Optimal Basic x 1 x 2 s 1 s 2 s 3 s 4 Solution z 0 0 1/3 4/3 0 0 12 2/3 x 2 0 1 0 0 0 2/3 -1/3 2/3 -1 1 -2/3 1/3 0 0 1 4/3 10/3 3 2/3 x 1 s 3 s 4 New pivot s 1 -Equation=old s 1 -Equation /1. 5 New z-Equation=old z-Equation – (-1/2) *new pivot equation New x 1 -Equation=old x 1 -Equation – (1/2) * new pivot equation New s 3 -Equation=old s 3 -Equation – (3/2) * new pivot equation New s 4 -Equation=old s 4 -Equation – (1) * new pivot equation x 1 =4/3, x 2=10/3, and z=38/3 (point C)

Interpreting the Simplex Tableau • • • The optimum solution The status of the resources The unit worth of the resources The sensitivity of the optimum solution to changes in the availability of resources, coefficients of the obj fcn, and usage of resources by activities The first three are in optimal solution of the simplex tableau Forth one needs additional computations

Summary • Simplex method was introduced as algebraic procedure for solving LP problems • Described how initial tableau of a linear program is a necessary step in the simplex solution procedure, including (≤), (≥), and (=) constraints into tableau form • Discussed how the special cases of infeasibility, unboundedness, multiple optimal solution, and degeneracy can occur with the simplex method

Special Cases in the Simplex Method • Special types of LP problems need special attentions • Special types: – More than one optimal solution – Infeasible problems – Unbounded solutions – Ties for pivot column and/or ties for the pivot row – Constraints with negative quantity values

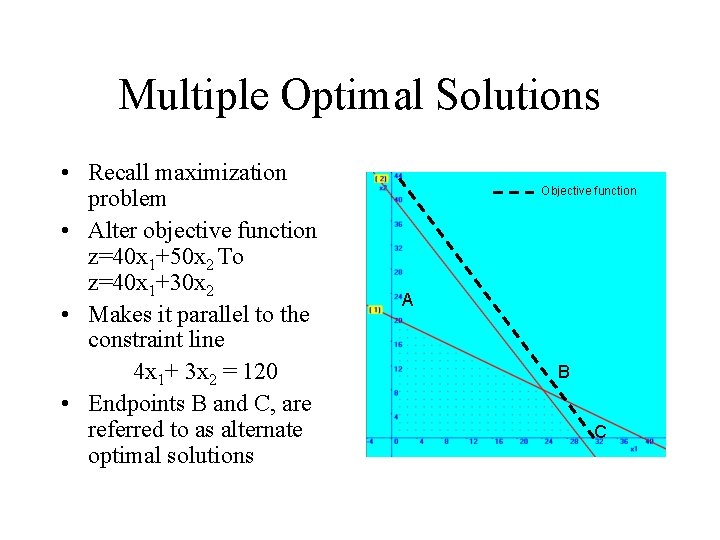
Multiple Optimal Solutions • Recall maximization problem • Alter objective function z=40 x 1+50 x 2 To z=40 x 1+30 x 2 • Makes it parallel to the constraint line 4 x 1+ 3 x 2 = 120 • Endpoints B and C, are referred to as alternate optimal solutions Objective function A B C

Multiple Solutions from the Simplex Not in solution Tableau • The optimal simplex tableau is: • How do we know that multiple optimal solution exist? • Determined from the row Z • Negative row Z values represent profit • Values of zero indicate no increase or loss • Coefficients of x 1 and s 1 have zero values • Coefficient of x 2 has a value of zero and it is not part of basic solution But has a 0 coef. Basic Z x 1 Z 1 0 s 1 0 0 x 1 0 1 s 2 Solution 0 10 1200 1. 25 1 -0. 25 10 0. 75 0 0. 25 30 x 2 0

Multiple Solutions from the Simplex Tableau (cont. ) • If x 2 enters solution, we will have a new solution without changing z • Multiple optimal solution is indicated by a value of zero in row Z for a nonbasic variable • To determine alternate solution, select x 2 as the entering variable and then determine pivot row as usual Basic Z x 1 x 2 s 1 s 2 Solutio n Z 1 0 0 0 10 1200 s 1 0 0 1. 2 5 1 -0. 25 10 x 1 0. 7 5 0 0. 25 30 Basic Z x 1 x 2 s 1 s 2 Solution Z 1 0 0 0 10 1200 x 2 0 0 1 0. 8 -0. 2 8 x 1 0 -0. 6 0. 4 24

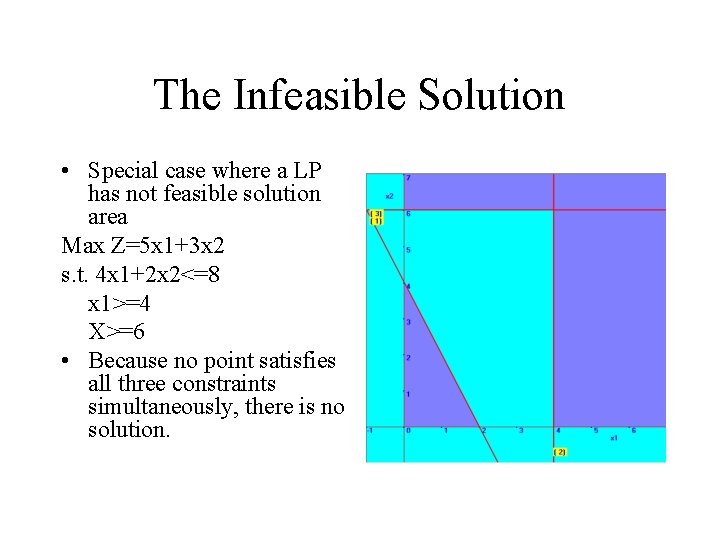
The Infeasible Solution • Special case where a LP has not feasible solution area Max Z=5 x 1+3 x 2 s. t. 4 x 1+2 x 2<=8 x 1>=4 X>=6 • Because no point satisfies all three constraints simultaneously, there is no solution.

The Infeasible Solution (cont. ) All values are zero or positive indicating that it is optimal • Solution: x 2=4, R 1=4, and R 2=2 – Existence of artificial variables in final tableau makes the solution meaningless • Occur as a result of making errors in defining problem correctly or in formulating the LP problem Basic Z x 1 x 2 s 1 s 2 s 3 R 1 R 2 Solution Z 1 M+1 0 M M 0. 5 M+1. 5 0 0 -0. 6 M+12 x 2 0 2 1 0 0 0. 5 0 0 4 R 1 0 -1 0 0 1 0 4 R 2 0 -2 0 0 -1 -0. 5 0 1 2

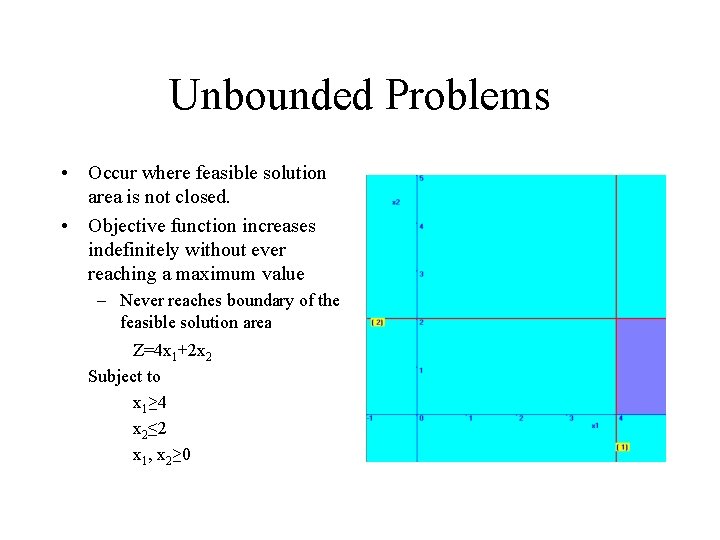
Unbounded Problems • Occur where feasible solution area is not closed. • Objective function increases indefinitely without ever reaching a maximum value – Never reaches boundary of the feasible solution area Z=4 x 1+2 x 2 Subject to x 1≥ 4 x 2≤ 2 x 1, x 2≥ 0

Unbounded Problems (cont. ) First tableau • In second tableau, s 1 is chosen as the entering variable because it has most negative coefficient in row Z • There is no leaving variable because one row value is -4 and the other is undefined • Indicates that solution is unbounded • A solution is unbounded if row value ratios are all negative or undefined • Occurs as a result of making errors in defining problem or in formulating LP problem Basic Z x 1 x 2 s 1 s 2 R 1 Solution Z 1 M-4 -2 M 0 0 -4 M R 1 0 -1 0 1 4 s 2 0 0 1 0 2 Second tableau Basic Z x 1 x 2 s 1 s 2 R 1 Solution Z 1 0 -2 -4 0 M+4 16 X 1 0 -1 0 1 4 s 2 0 0 1 0 2

Degeneracy • Possible to have a tie for pivot row • A tie should be broken arbitrarily • Other choice for leaving variable will posses a zero value in next tableau • Solution is said to be degenerate – Z value never improves • An example of a degeneracy condition Maximize Z = 4 x 1+ 6 x 2 subject to 6 x 1+ 4 x 2 ≤ 24 x 2 ≤ 3 5 x 1+10 x 2 ≤ 40

Tie for the Pivot Row • In second tableau, we will see a tie for pivot row between s 1, and s 3 rows • S 3 row is selected arbitrarily, the resulting third tableau will be shown Basic Z x 1 x 2 s 1 s 2 s 3 Solution Z 1 -4 0 0 6 0 18 s 1 0 6 0 1 -4 0 12 x 2 0 0 1 0 3 s 3 0 5 0 0 -10 1 10 S 1 ratio: 12/6 =2 S 3 ratio: 10/5 =2

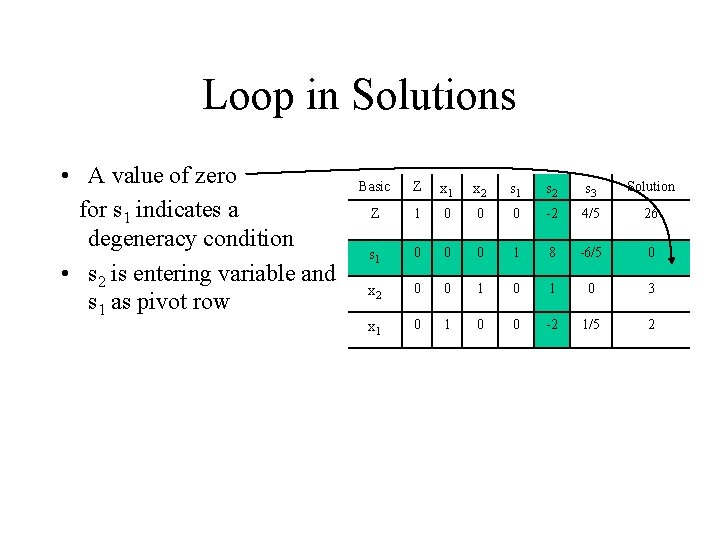
Loop in Solutions • A value of zero for s 1 indicates a degeneracy condition • s 2 is entering variable and s 1 as pivot row Basic Z x 1 x 2 s 1 s 2 s 3 Solution Z 1 0 0 0 -2 4/5 26 s 1 0 0 0 1 8 -6/5 0 x 2 0 0 1 0 3 x 1 0 0 -2 1/5 2

Loops in Solutions (Cont. ) • Optimal solution did not change • Graphical analysis of this problem is shown in the next slide Basic Z x 1 x 2 s 1 s 2 s 3 Solution Z 1 0 0 1/4 0 1/2 26 s 2 0 0 0 1/8 1 -3/20 0 x 2 0 0 1 -1/8 0 3/20 3 x 1 0 1/4 0 -1/10 2

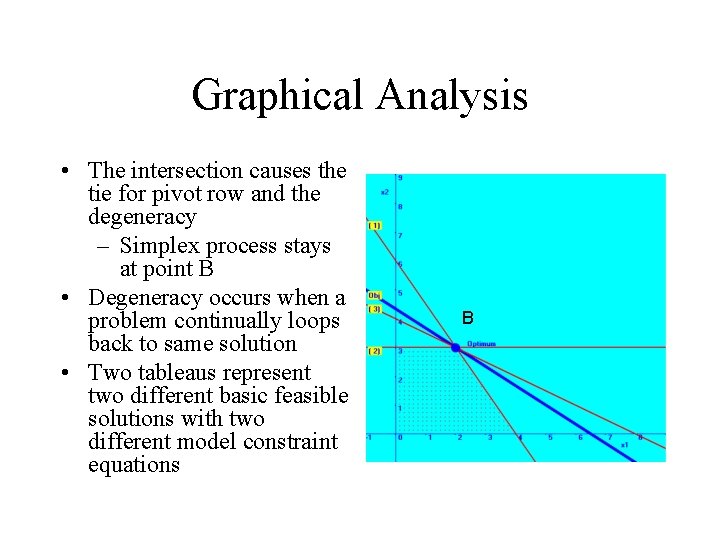
Graphical Analysis • The intersection causes the tie for pivot row and the degeneracy – Simplex process stays at point B • Degeneracy occurs when a problem continually loops back to same solution • Two tableaus represent two different basic feasible solutions with two different model constraint equations B

HW Assignments 1. Problem set 3. 2 A, problem 2, part a, b, and c. 2. Given the following linear programming model: Min Z=4 x 1+x 2 s. t. 3 x 1+6 x 2>=15 8 x 1+2 x 2>=12 x 1, x 2>=0 Solve graphically and using the simplex method. What type of special case is this problem? Explain? 3. Transform the following linear programming model into proper form and setup the initial tableau. Do not solve it. Min Z=40 x 1+55 x 2+30 x 3 s. t. x 1+2 x 2+3 x 3 <=60 2 x 1+x 2+x 3 = 40 x 1+3 x 2+x 3>=50 5 x 2+x 3>=100 x 1, x 2, x 3>=0 4. Given the following linear programming model: Max Z=x 1+2 x 2 -x 3 s. t. 4 x 2+x 3<=40 x 1 -x 2<=20 2 x 1+4 x 2+3 x 3<=60 x 1, x 2, x 3>=0 Solve this problem using the simplex method. What type of special case is this problem? Explain?