Solving Linear Inequalities and Compound Inequalities Inequality Symbols

Solving Linear Inequalities and Compound Inequalities

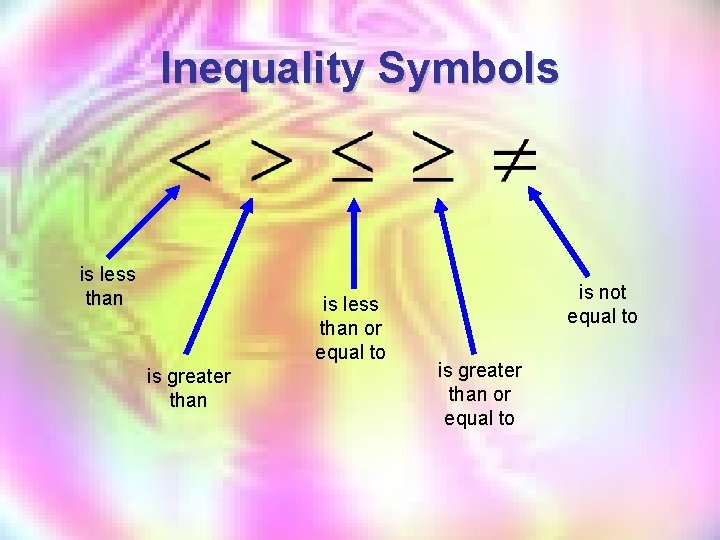
Inequality Symbols is less than or equal to is greater than is not equal to is greater than or equal to

Linear Inequality • Can be written in the form ax+b<0, ax+b>0, ax+b≤ 0, or ax+b≥ 0 where a and b are real numbers and a≠ 0 • Has one variable to the first power. for example: 2 x-3<8 • A solution is a value of the variable that makes the inequality true. x could equal -3, 0, 1, etc.

Transformations for Inequalities • Add/subtract the same number on each side of an inequality • Multiply/divide by the same positive number on each side of an inequality • If you multiply or divide by a negative number, you MUST flip the inequality sign!

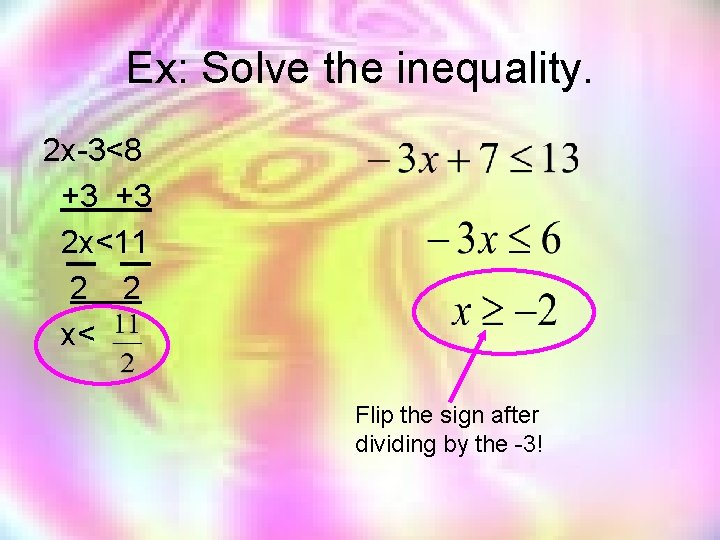
Ex: Solve the inequality. 2 x-3<8 +3 +3 2 x<11 2 2 x< Flip the sign after dividing by the -3!

Graphing Linear Inequalities • Remember: < and > signs will have an open circle and signs will have a closed circle graph of 4 5 6 graph of 7 -3 -2 -1 0

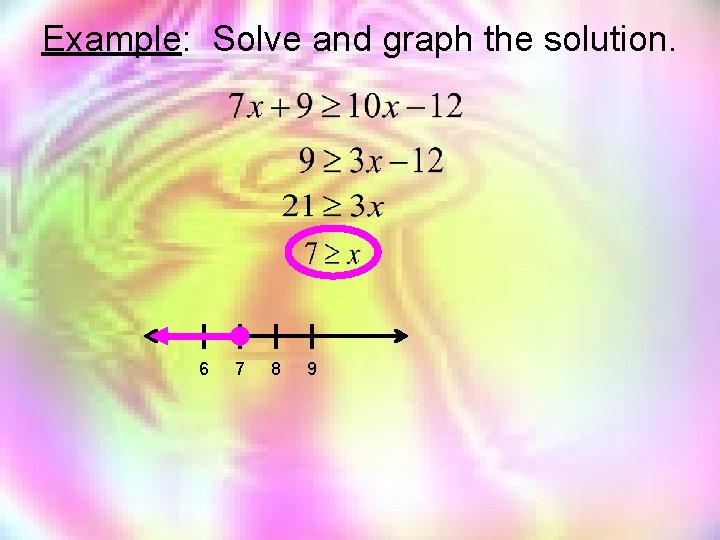
Example: Solve and graph the solution. 6 7 8 9

Example: Solve and graph the solution. This is a true statement, therefore the solution is ALL REAL NUMBERS.

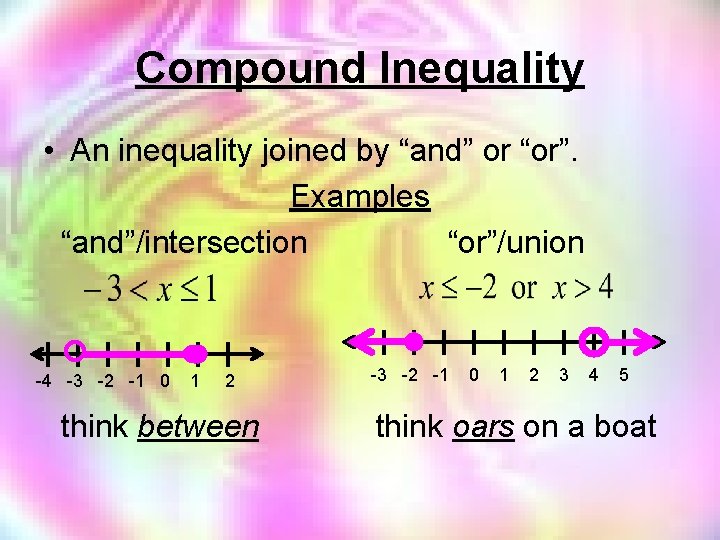
Compound Inequality • An inequality joined by “and” or “or”. Examples “and”/intersection “or”/union -4 -3 -2 -1 0 1 2 think between -3 -2 -1 0 1 2 3 4 5 think oars on a boat

Example: Solve & graph. -9 < t+4 < 10 -4 -4 -4 -13 < t < 6 Think between! -13 6

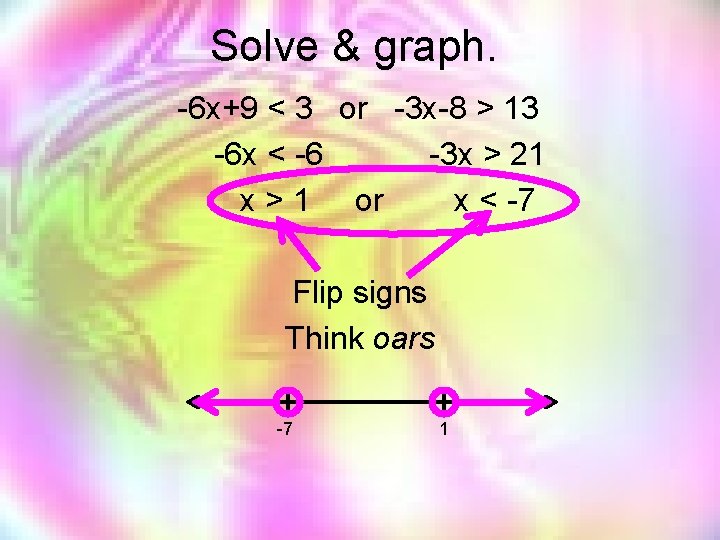
Solve & graph. -6 x+9 < 3 or -3 x-8 > 13 -6 x < -6 -3 x > 21 x > 1 or x < -7 Flip signs Think oars -7 1

Assignment p. 45 -46 #12 -33 m 3, 42, 48, 51, 53, 56