SOLVING LINEAR EQUATIONS WITH ONE VARIABLE PART II

SOLVING LINEAR EQUATIONS WITH ONE VARIABLE PART II Presented by Mr. Laws Math 1/JCMS

Goal/Objective ■ A-REI. 3 – Solve linear equations and inequalities in one variable.

Essential Question n Using math principles, how can we find the solution of linear equations with one variable?

Key Vocabulary Combine Like Terms Distributive Property Equation Linear Multi-Step Equations Properties of Equality Solution Variable

Linear Equations w/one variable ■ Linear equations in one variable can have one solution, infinity solutions, or no solution. ■ Multistep equations are mostly associated with these solutions and require specific procedures to solve the equation. ■ Using Distributive Property and Combining like terms is an important procedure to help solve multistep equations.

Linear Equations w/one variable ■ Key step to remember is to isolate the variable on one side of the equation and solve for the variable. ■ Make sure you have variables on one side of the equal sign and constants (numbers) on the other side of the equal sign. ■ You must use the Property of Equality to move variables or constants across the equal sign.

Distributive Property ■ Distributive Property requires you to multiply what’s in the parenthesis by what outside the parenthesis. It is written in the form of: a(b +c) = ab + ac Or (b + c)a = ba + ca Example: 5(a + 2) = 5 a + 10 or (3 + x)2 = 6 + 2 x

Multi-Step Equations/Combining Like Terms ■ A multistep equations, requires more than two steps to find the solution or solve. ■ When solving multistep equations, you might have to use the distribute property and/or combine like terms ■ Remember only like (same) terms can be combined such as, variables and constants. ■ For example: 6(x + 4) – 4 x = 6 x – 4 What is the first step to take to solve this equation?

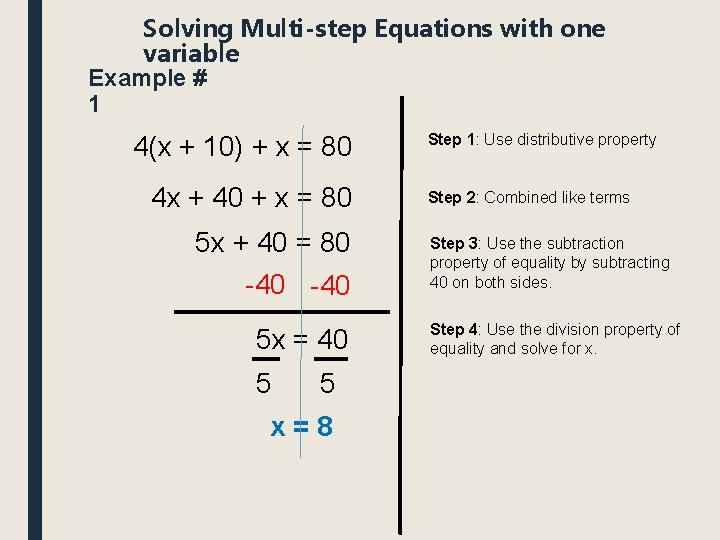
Solving Multi-step Equations with one variable Example # 1 4(x + 10) + x = 80 4 x + 40 + x = 80 5 x + 40 = 80 -40 5 x = 40 5 5 x=8 Step 1: Use distributive property Step 2: Combined like terms Step 3: Use the subtraction property of equality by subtracting 40 on both sides. Step 4: Use the division property of equality and solve for x.

Solving Multi-step Equations with one variable Example # 2 6 a – 8 – 4 a = 32 2 a – 8 = 32 +8 +8 2 a = 40 2 2 x = 20 Step 1: Combined like terms Step 2: Use the addition property of equality by adding 8 on both sides. Step 3: Use the division property of equality and solve for a.

Solving Multi-step Equations with one variable on both sides. Example # 3 -3 y – 24 = 5 y – 8 +24 -3 y = 5 y + 16 -5 y -8 y = 16 -8 -8 y = -2 Step 1: Use the addition property of equality by add 24 on both sides. Step 2: Subtract -5 y on both sides of the equal sign. Step 3: Use the division property of equality and solve for x. by dividing -8 on both sides.

Solving Multi-step Equations with one variable on both sides. Example # 4 6(x + 4) – 4 x = 6 x – 4 Step 1: Use distributive property 6 x + 24 – 4 x = 6 x – 4 Step 2: Combined like terms 2 x + 24 = 6 x – 4 -24 2 x = 6 x – 28 -6 x -4 x = -28 -4 -4 x=7 Step 3: Use the subtraction property of equality by subtracting 24 on both sides. Step 4: Subtract -6 x on both sides of the equal sign. Step 5: Use the division property of equality and solve for x by dividing -4 on both sides of the equal sign.

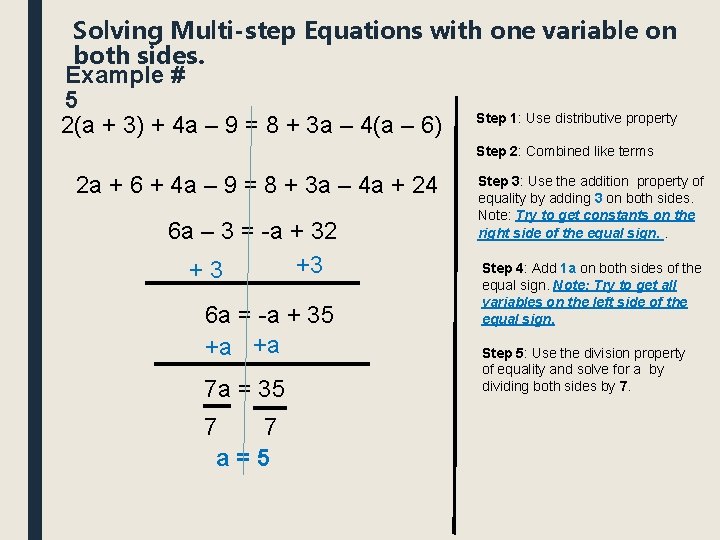
Solving Multi-step Equations with one variable on both sides. Example # 5 2(a + 3) + 4 a – 9 = 8 + 3 a – 4(a – 6) Step 1: Use distributive property Step 2: Combined like terms 2 a + 6 + 4 a – 9 = 8 + 3 a – 4 a + 24 6 a – 3 = -a + 32 +3 +3 6 a = -a + 35 +a +a 7 a = 35 7 7 a=5 Step 3: Use the addition property of equality by adding 3 on both sides. Note: Try to get constants on the right side of the equal sign. . Step 4: Add 1 a on both sides of the equal sign. Note: Try to get all variables on the left side of the equal sign. Step 5: Use the division property of equality and solve for a by dividing both sides by 7.

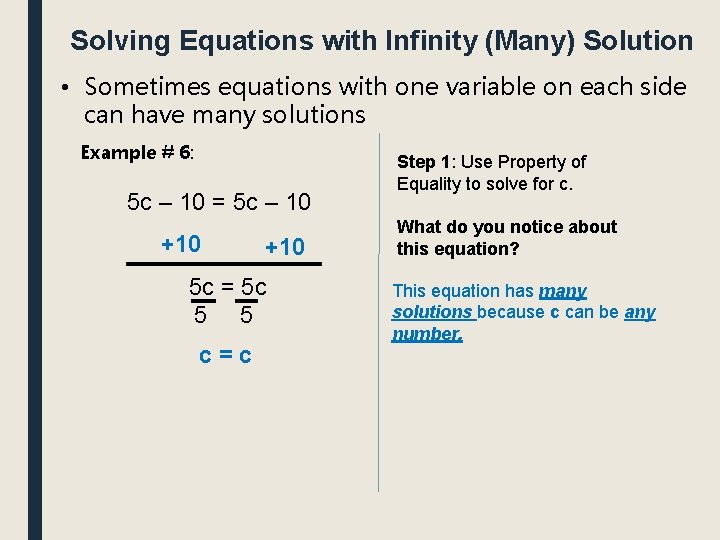
Solving Equations with Infinity (Many) Solution • Sometimes equations with one variable on each side can have many solutions Example # 6: 5 c – 10 = 5 c – 10 +10 5 c = 5 c 5 5 c=c Step 1: Use Property of Equality to solve for c. What do you notice about this equation? This equation has many solutions because c can be any number.

Evaluating equations with No Solution • Sometimes multistep equations can have no solution. Example # 7 7 + 6(x + 8) = 6 x +10 What is the 1 st step? 7 + 6 x + 48 = 6 x +10 What is the 2 nd step? 6 x + 55 = 6 x +10 - 6 x -6 x 55 = 10 What is the 3 rd step? Did you notice that the variable where the same? • By subtracting -6 x from both sides, the equation is left with 55 = 10. • This is not true, so this equation has no solution.

Summary ■ What have you learned about this lesson? ■ What are some important steps to remember when solving multistep equations? ■ Make sure you review your notes, additional questions or notes, and write a summary or reflection.

Your Turn • Solve each equation below. SHOW YOUR WORK!!!! 1. 4(a + 2) = 8(4 – 2) 2. 2 p – 9 = 3 – 2 p 3. 11 – 3(w + 2) = 7 – (4 w + 5) 4. 3(b + 4) – 2 = 2(2 b + 5) – b 5. 2 x + 1 – 3 x + 5 = 3(x +10) 6. 3(x – 2) + 1 = 2(x – 4) + x + 13