Solving Linear Equations What is an Equation Linear


























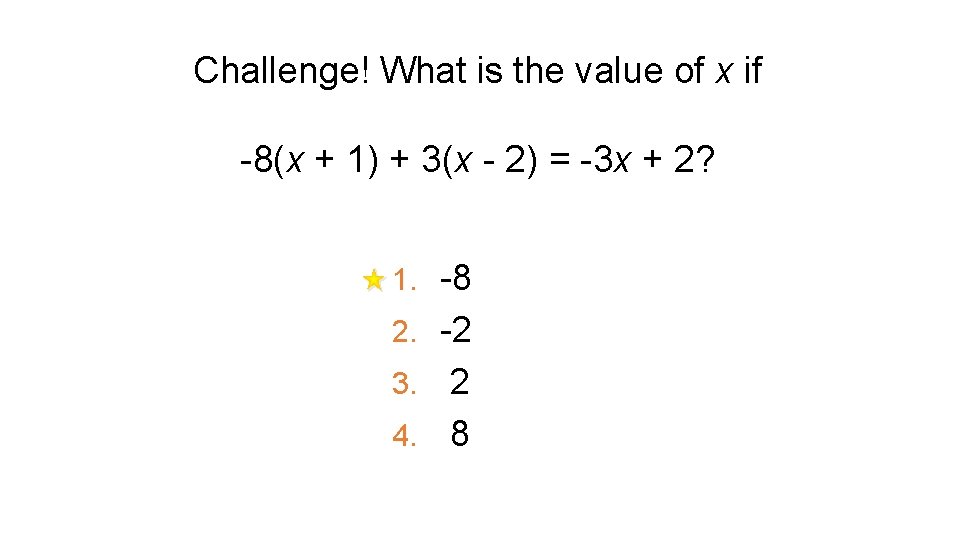


- Slides: 30

Solving Linear Equations

What is an Equation?

Linear Equations

Sides of an Equation LHS RHS The purpose of solving an equation is to find the value or values of the variable that will make the equation true, i. e. makes the left hand side equal to the right hand side.

Solving an Equation

Solve these using Inspection or Trial and Error

Maintaining the Balance When solving an equation of any form, we perform operations on both sides of the equation. Our aim is to isolate the variable on its own on the LHS. The same operation must occur on both the left hand side, and the right hand side. In effect, we are keeping the equation balanced.

Maintaining the Balance

Undoing operations This process of maintaining the balance (or equality), can also be looked at as the process of ‘undoing’ the operation being applied to the variable. + and - are opposites �and are opposites x 2 and √ are opposites

1 – step Equations that take only 1 step to solve

1 Step Equations For basic examples only one step is required

1 Step Equations

1 Step Equations

1 Step Equations

2 – step Equations that take 2 steps to solve

2 Step Equations

2+ Step Equations – more than 2 steps

Flowchart Diagram

Equations with variables on both sides These require to isolate the variable on one side, and the constant on the other

Example This has the variable x on both sides. It doesn’t matter which one you move, however it is preferred you move the one that keeps the variable positive. Add 3 x to both sides (RHS x is positive) Simplify Subtract 1 from both sides Simplify Swap sides so x is on the LHS Divide both sides by 5 ANSWER

Example Solve 8 y – 9 = -3 y + 2 11 y – 9 = 2 11 y = 11 y=1 By adding 3 y to both sides we get a positive y variable on the LHS – yes! Add 3 y to both sides and simplify Add 9 to both sides and simplify Divide both sides by 11 ANSWER We should really check our answer by substituting our answer back into the original equation 8 � 1 – 9 = -3 � 1 + 2 8 – 9 = -3 +2 -1 = -1 Matches, therefore our answer is correct!!

What is the value of x if 1. -3 2. 3. 4. 3 3 - 4 x = 18 + x?

Equations Involving brackets These require the expansion of the brackets, before collecting like terms

Example Solve 3(x – 2) = 6 x + 3 3 x - 6 = 6 x + 3 3 x + 3 = -6 3 x = -9 x = -3 This requires the brackets to be expanded Expanded out Subtracted 3 x from both sides, and swapped so the x term is on the LHS Subtract 3 from both sides Divide both sides by 3 ANSWER

Example Solve 5(x – 3) + 3 x = -7 5 x – 15 + 3 x = -7 8 x -15 = -7 8 x = 8 x=1 This requires the brackets to be expanded Expanded out Group like terms (for x) together Add 15 to both sides Divide both sides by 8 ANSWER

Example Solve 4(2 x – 1) + 5 = 2(3 x – 1) 8 x – 4 + 5 = 6 x - 2 2 x + 1 = -2 2 x = -3/2 This requires the brackets to be expanded Expanded out both sides Group like terms (for x) together on LHS Subtract 1 from both sides Divide both sides by 2 ANSWER

Example Sometimes you can choose whether or not to expand the brackets Solve 6(2 x + 1) = 12 ÷ 6 2 x + 1 = 2 -1 -1 2 x = 1 ÷ 2 x = 1/2 or Solve 6(2 x + 1) = 12 Expand out 12 x + 6 = 12 -6 -6 12 x = 6 ÷ 12 x = 1/2 Same answer, but two different ways of getting there
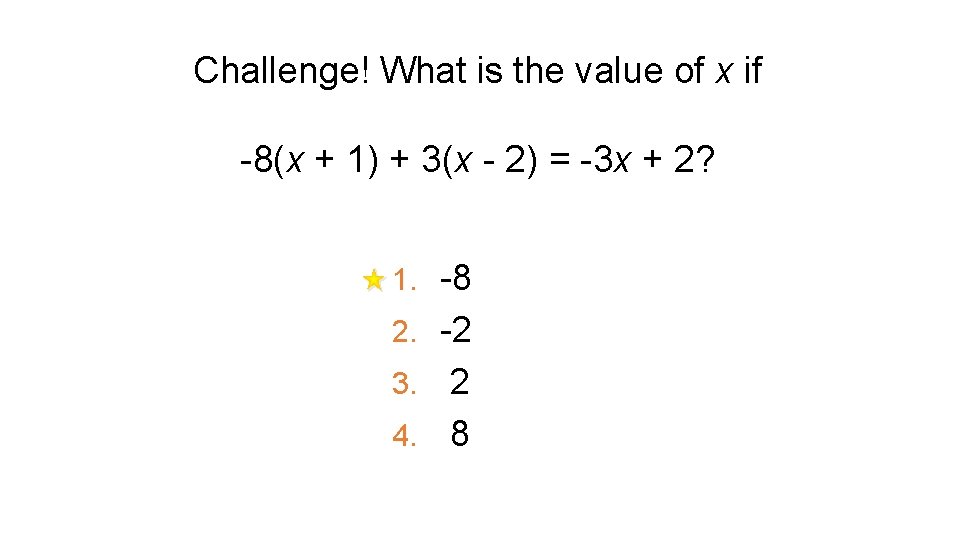
Challenge! What is the value of x if -8(x + 1) + 3(x - 2) = -3 x + 2? 1. -8 2. -2 2 4. 8 3.

Special Case #1 Solve 2 x + 5 = 2 x – 3 5 = -3 This is never true NO SOLUTION Special Case #2 Solve 3(x + 1) - 5 = 3 x – 2 3 x + 3 – 5 = 3 x – 2 -2 = -2 This is always true INFINITE SOLUTIONS

Homework Solving Linear Equations Exercise L: Page 51