Solving Linear Equations and 2 1 Inequalities Solving





































































- Slides: 74

Solving Linear Equations and 2 -1 Inequalities Solving Linear Equations and Inequalities Warm Up Lesson Presentation Lesson Quiz Holt Algebra 22

2 -1 Solving Linear Equations and Inequalities Warm Up Simplify each expression. 2. –(w – 2) –w + 2 1. 2 x + 5 – 3 x –x + 5 3. 6(2 – 3 g) 12 – 18 g Graph on a number line. 4. t > – 2 – 4 – 3 – 2 – 1 0 1 2 3 4 5 5. Is 2 a solution of the inequality – 2 x < – 6? Explain. No; when 2 is substituted for x, the inequality is false: – 4 < – 6 Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Objectives Solve linear equations using a variety of methods. Solve linear inequalities. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Vocabulary equation solution set of an equation linear equation in one variable identify contradiction inequality Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities An equation is a mathematical statement that two expressions are equivalent. The solution set of an equation is the value or values of the variable that make the equation true. A linear equation in one variable can be written in the form ax = b, where a and b are constants and a ≠ 0. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Linear Equations in One variable 4 x = 8 3 x – = – 9 2 x – 5 = 0. 1 x +2 Nonlinear Equations + 1 = 32 + 1 = 41 3 – 2 x = – 5 Notice that the variable in a linear equation is not under a radical sign and is not raised to a power other than 1. The variable is also not an exponent and is not in a denominator. Solving a linear equation requires isolating the variable on one side of the equation by using the properties of equality. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities To isolate the variable, perform the inverse or opposite of every operation in the equation on both sides of the equation. Do inverse operations in the reverse order of operations. Holt Algebra 2

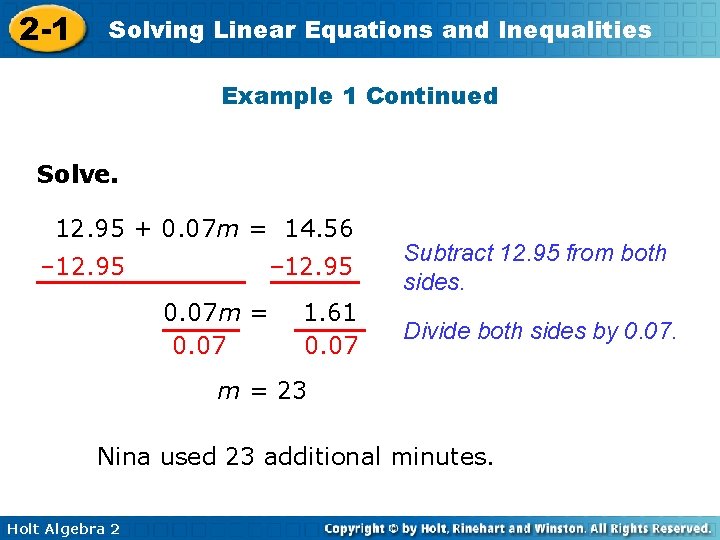
2 -1 Solving Linear Equations and Inequalities Example 1: Consumer Application The local phone company charges $12. 95 a month for the first 200 of air time, plus $0. 07 for each additional minute. If Nina’s bill for the month was $14. 56, how many additional minutes did she use? Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 1 Continued Let m represent the number of additional minutes that Nina used. Model monthly plus charge 12. 95 Holt Algebra 2 + additional minute charge times 0. 07 * number of additional = total charge minutes m = 14. 56

2 -1 Solving Linear Equations and Inequalities Example 1 Continued Solve. 12. 95 + 0. 07 m = 14. 56 – 12. 95 0. 07 m = 0. 07 1. 61 0. 07 Subtract 12. 95 from both sides. Divide both sides by 0. 07. m = 23 Nina used 23 additional minutes. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 1 Stacked cups are to be placed in a pantry. One cup is 3. 25 in. high and each additional cup raises the stack 0. 25 in. How many cups fit between two shelves 14 in. apart? Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 1 Continued Let c represent the number of additional cups needed. Model additional cup one cup plus height 3. 25 Holt Algebra 2 + 0. 25 times * number of total additional = height cups c = 14. 00

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 1 Continued Solve. 3. 25 + 0. 25 c = 14. 00 – 3. 25 0. 25 c = 10. 75 0. 25 Subtract 3. 25 from both sides. Divide both sides by 0. 25. c = 43 44 cups fit between the 14 in. shelves. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 2: Solving Equations with the Distributive Property Solve 4(m + 12) = – 36 Method 1 The quantity (m + 12) is multiplied by 4, so divide by 4 first. 4(m + 12) = – 36 4 4 m + 12 = – 9 – 12 m = – 21 Holt Algebra 2 Divide both sides by 4. Subtract 12 from both sides.

2 -1 Solving Linear Equations and Inequalities Example 2 Continued Check 4(m + 12) = – 36 4(– 21 + 12) 4(– 9) – 36 Holt Algebra 2 – 36

2 -1 Solving Linear Equations and Inequalities Example 2 Continued Solve 4(m + 12) = – 36 Method 2 Distribute before solving. 4 m + 48 = – 36 – 48 Distribute 4. Subtract 48 from both sides. 4 m = – 84 4 m – 84 = 4 4 m = – 21 Holt Algebra 2 Divide both sides by 4.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 a Solve 3(2 – 3 p) = 42. Method 1 The quantity (2 – 3 p) is multiplied by 3, so divide by 3 first. 3(2 – 3 p) = 42 3 3 2 – 3 p = 14 – 2 – 3 p = 12 – 3 p = – 4 Holt Algebra 2 Divide both sides by 3. Subtract 2 from both sides. Divide both sides by – 3.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 a Continued Check 3(2 – 3 p) = 42 3(2 + 12) 6 + 36 42 Holt Algebra 2 42 42 42

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 a Continued Solve 3(2 – 3 p) = 42. Method 2 Distribute before solving. 6 – 9 p = 42 – 6 – 9 p = 36 – 9 p 36 = – 9 p = – 4 Holt Algebra 2 Distribute 3. Subtract 6 from both sides. Divide both sides by – 9.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 b Solve – 3(5 – 4 r) = – 9. Method 1 The quantity (5 – 4 r) is multiplied by – 3, so divide by – 3 first. – 3(5 – 4 r) = – 9 – 3 5 – 4 r = 3 – 5 – 4 r = – 2 Holt Algebra 2 Divide both sides by – 3. Subtract 5 from both sides.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 b Continued Solve – 3(5 – 4 r) = – 9. Method 1 – 4 r – 2 – 4 r= Divide both sides by – 4. = Check – 3(5 – 4 r) = – 9 – 3(5 – 4 • ) – 9 – 3(5 – 2) – 3(3) – 9 Holt Algebra 2 – 9 – 9

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 b Continued Solve – 3(5 – 4 r) = – 9. Method 2 Distribute before solving. – 15 + 12 r = – 9 +15 12 r = 6 12 r 6 = 12 12 r= Holt Algebra 2 Distribute 3. Add 15 to both sides. Divide both sides by 12.

2 -1 Solving Linear Equations and Inequalities If there are variables on both sides of the equation, (1) simplify each side. (2) collect all variable terms on one side and all constants terms on the other side. (3) isolate the variables as you did in the previous problems. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 3: Solving Equations with Variables on Both Sides Solve 3 k– 14 k + 25 = 2 – 6 k – 12. Simplify each side by combining – 11 k + 25 = – 6 k – 10 like terms. +11 k Collect variables on the right side. Add. 25 = 5 k – 10 Collect constants on the left side. +10 + 10 35 = 5 k 5 5 7=k Holt Algebra 2 Isolate the variable.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 3 Solve 3(w + 7) – 5 w = w + 12. Simplify each side by combining – 2 w + 21 = w + 12 like terms. +2 w Collect variables on the right side. 21 = – 12 9 3 Holt Algebra 2 3 w + 12 – 12 = 3 w 3 3=w Add. Collect constants on the left side. Isolate the variable.

2 -1 Solving Linear Equations and Inequalities You have solved equations that have a single solution. Equations may also have infinitely many solutions or no solution. An equation that is true for all values of the variable, such as x = x, is an identity. An equation that has no solutions, such as 3 = 5, is a contradiction because there are no values that make it true. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 4 A: Identifying Identities and Contractions Solve 3 v – 9 – 4 v = –(5 + v) – 9 – v = – 5 – v +v +v – 9 ≠ – 5 x Simplify. Contradiction The equation has no solution. The solution set is the empty set, which is represented by the symbol. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 4 B: Identifying Identities and Contractions Solve 2(x – 6) = – 5 x – 12 + 7 x Simplify. 2 x – 12 = 2 x – 12 – 2 x – 12 = – 12 Identity The solutions set is all real number, or . Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 4 a Solve 5(x – 6) = 3 x – 18 + 2 x 5 x – 30 = 5 x – 18 – 5 x Simplify. – 5 x – 30 ≠ – 18 x Contradiction The equation has no solution. The solution set is the empty set, which is represented by the symbol. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 4 b Solve 3(2 – 3 x) = – 7 x – 2(x – 3) 6 – 9 x = – 9 x + 6 Simplify. + 9 x +9 x 6=6 Identity The solutions set is all real numbers, or . Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities An inequality is a statement that compares two expressions by using the symbols <, >, ≤, ≥, or ≠. The graph of an inequality is the solution set, the set of all points on the number line that satisfy the inequality. The properties of equality are true for inequalities, with one important difference. If you multiply or divide both sides by a negative number, you must reverse the inequality symbol. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities These properties also apply to inequalities expressed with >, ≥, and ≤. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Helpful Hint To check an inequality, test • the value being compared with x • a value less than that, and • a value greater than that. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 5: Solving Inequalities Solve and graph 8 a – 2 ≥ 13 a + 8 – 13 a – 5 a – 2 ≥ 8 +2 +2 – 5 a ≥ 10 – 5 a ≤ 10 – 5 a ≤ – 2 Holt Algebra 2 Subtract 13 a from both sides. Add 2 to both sides. Divide both sides by – 5 and reverse the inequality.

2 -1 Solving Linear Equations and Inequalities Example 5 Continued Solve and graph 8 a – 2 ≥ 13 a + 8. Check Test values in the original inequality. Test x = – 4 • – 10 – 9 Test x = – 2 – 8 – 7 – 6 – 5 – 4 – 3 – 2 – 1 Test x = – 1 8(– 4) – 2 ≥ 13(– 4) + 8 8(– 2) – 2 ≥ 13(– 2) + 8 8(– 1) – 2 ≥ 13(– 1) + 8 – 34 ≥ – 44 So – 4 is a solution. Holt Algebra 2 – 18 ≥ – 18 So – 2 is a solution. – 10 ≥ – 5 x So – 1 is not a solution.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 5 Solve and graph x + 8 ≥ 4 x + 17 –x –x 8 ≥ 3 x +17 – 9 ≥ 3 x 3 3 – 3 ≥ x or x ≤ – 3 Holt Algebra 2 Subtract x from both sides. Subtract 17 from both sides. Divide both sides by 3.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 5 Continued Solve and graph x + 8 ≥ 4 x + 17. Check Test values in the original inequality. Test x = – 6 • – 6 – 5 Test x = – 3 – 6 + 8 ≥ 4(– 6) + 17 – 3 +8 ≥ 4(– 3) + 17 2 ≥ – 7 So – 6 is a solution. Holt Algebra 2 5≥ 5 So – 3 is a solution. – 4 – 3 – 2 – 1 0 1 2 3 Test x = 0 0 +8 ≥ 4(0) + 17 8 ≥ 17 x So 0 is not a solution.

2 -1 Solving Linear Equations and Inequalities Lesson Quiz: Part I 1. Alex pays $19. 99 for cable service each month. He also pays $2. 50 for each movie he orders through the cable company’s pay-per-view service. If his bill last month was $32. 49, how many movies did Alex order? 5 movies Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Lesson Quiz: Part II Solve. x=6 2. 2(3 x – 1) = 34 3. 4 y – 9 – 6 y = 2(y + 5) – 3 y = – 4 4. r + 8 – 5 r = 2(4 – 2 r) all real numbers, or 5. – 4(2 m + 7) = no solution, or Holt Algebra 2 (6 – 16 m)

2 -1 Solving Linear Equations and Inequalities Lesson Quiz: Part III 5. Solve and graph. 12 + 3 q > 9 q – 18 q<5 ° – 2 – 1 Holt Algebra 2 0 1 2 3 4 5 6 7

Linear Equations and Inequalities 2 -1 2 -2 Solving Proportional Reasoning Warm Up Lesson Presentation Lesson Quiz Holt Algebra 22

2 -1 Solving Linear Equations and Inequalities Warm Up Write as a decimal and a percent. 1. 0. 4; 40% 2. 1. 875; 187. 5% Holt Algebra 2

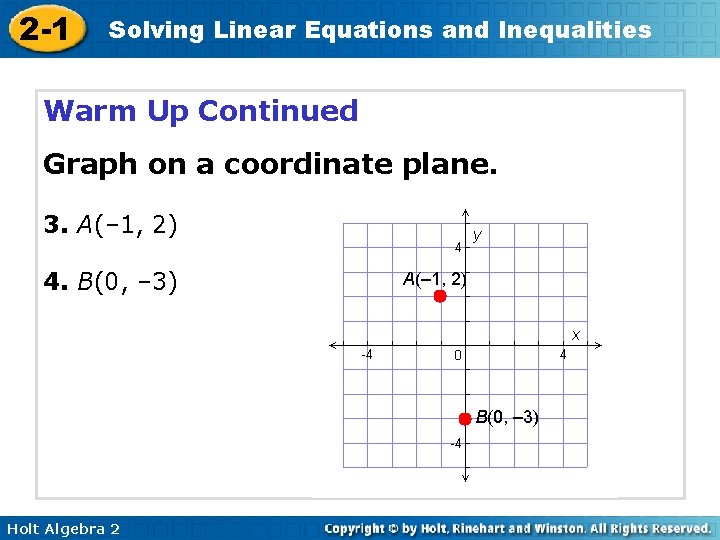
2 -1 Solving Linear Equations and Inequalities Warm Up Continued Graph on a coordinate plane. 3. A(– 1, 2) 4. B(0, – 3) A(– 1, 2) B(0, – 3) Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Warm Up Continued 5. The distance from Max’s house to the park is 3. 5 mi. What is the distance in feet? (1 mi = 5280 ft) 18, 480 ft Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Objective Apply proportional relationships to rates, similarity, and scale. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Vocabulary ratio proportion rate similar indirect measurement Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Recall that a ratio is a comparison of two numbers by division and a proportion is an equation stating that two ratios are equal. In a proportion, the cross products are equal. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities If a proportion contains a variable, you can cross multiply to solve for the variable. When you set the cross products equal, you create a linear equation that you can solve by using the skills that you learned in Lesson 2 -1. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Reading Math In a ÷ b = c ÷ d, b and c are the means, and a and d are the extremes. In a proportion, the product of the means is equal to the product of the extremes. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 1: Solving Proportions Solve each proportion. A. 16 = 24 p 12. 9 B. 16 24 = p 12. 9 206. 4 = 24 p 206. 4 24 p = 24 24 8. 6 = p Holt Algebra 2 14 c = 88 132 Set cross products equal. Divide both sides. 88 c = 1848 88 88 c = 21

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 1 Solve each proportion. A. y 77 = 12 84 B. y 77 = 12 84 924 = 84 y 924 84 y = 84 84 11 = y Holt Algebra 2 15 2. 5 = x 7 Set cross products equal. Divide both sides. 2. 5 x =105 2. 5 x = 2. 5 105 2. 5 x = 42

2 -1 Solving Linear Equations and Inequalities Because percents can be expressed as ratios, you can use the proportion to solve percent problems. Remember! Percent is a ratio that means per hundred. For example: 30% = 0. 30 = 30 100 Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 2: Solving Percent Problems A poll taken one day before an election showed that 22. 5% of voters planned to vote for a certain candidate. If 1800 voters participated in the poll, how many indicated that they planned to vote for that candidate? You know the percent and the total number of voters, so you are trying to find the part of the whole (the number of voters who are planning to vote for that candidate). Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 2 Continued Method 1 Use a proportion. Method 2 Use a percent equation. Divide the percent by 100. Percent (as decimal) whole = part 0. 225 1800 = x 22. 5(1800) = 100 x Cross multiply. 405 = x Solve for x. x = 405 So 405 voters are planning to vote for that candidate. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 At Clay High School, 434 students, or 35% of the students, play a sport. How many students does Clay High School have? You know the percent and the total number of students, so you are trying to find the part of the whole (the number of students that Clay High School has). Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 Continued Method 1 Use a proportion. Method 2 Use a percent equation. 35% = 0. 35 Divide the percent by 100. Percent (as decimal) whole = part 100(434) = 35 x Cross multiply. 0. 35 x = 434 x = 1240 Solve for x. x = 1240 Clay High School has 1240 students. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities A rate is a ratio that involves two different units. You are familiar with many rates, such as miles per hour (mi/h), words per minute (wpm), or dollars per gallon of gasoline. Rates can be helpful in solving many problems. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 3: Fitness Application Ryan ran 600 meters and counted 482 strides. How long is Ryan’s stride in inches? (Hint: 1 m ≈ 39. 37 in. ) Use a proportion to find the length of his stride in meters. 600 m xm = 482 strides 1 stride 600 = 482 x x ≈ 1. 24 m Holt Algebra 2 meters Write both ratios in the form strides. Find the cross products.

2 -1 Solving Linear Equations and Inequalities Example 3: Fitness Application continued Convert the stride length to inches. 39. 37 in. 1 m 1. 24 m 1 stride length is the conversion factor. 39. 37 in. ≈ 49 in. 1 m 1 stride length Ryan’s stride length is approximately 49 inches. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 3 Luis ran 400 meters in 297 strides. Find his stride length in inches. Use a proportion to find the length of his stride in meters. 400 m xm = 297 strides 1 stride 400 = 297 x x ≈ 1. 35 m Holt Algebra 2 meters Write both ratios in the form strides. Find the cross products.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 3 Continued Convert the stride length to inches. 39. 37 in. 1 m is the conversion factor. 1. 35 m 53 in. 39. 37 in. ≈ 1 stride length 1 m 1 stride length Luis’s stride length is approximately 53 inches. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Similar figures have the same shape but not necessarily the same size. Two figures are similar if their corresponding angles are congruent and corresponding sides are proportional. Reading Math The ratio of the corresponding side lengths of similar figures is often called the scale factor. Holt Algebra 2

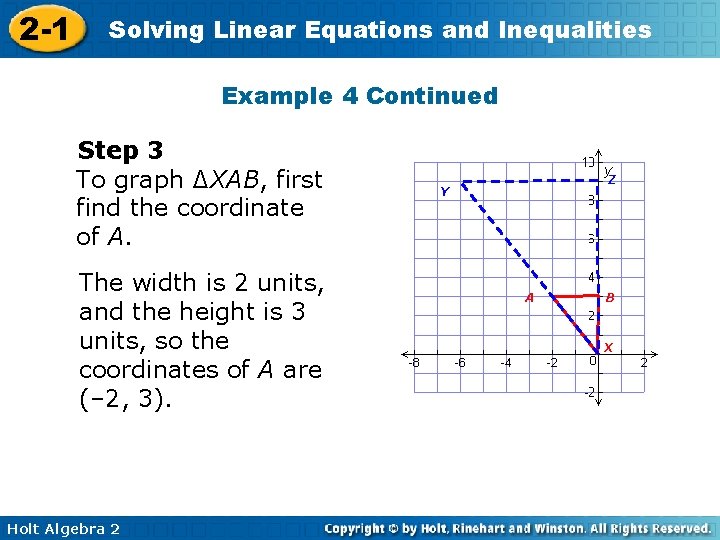
2 -1 Solving Linear Equations and Inequalities Example 4: Scaling Geometric Figures in the Coordinate Plane ∆XYZ has vertices X(0, 0), Y(– 6, 9) and Z(0, 9). ∆XAB is similar to ∆XYZ with a vertex at B(0, 3). Graph ∆XYZ and ∆XAB on the same grid. Step 1 Graph ∆XYZ. Then draw XB. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 4 Continued Step 2 To find the width of ∆XAB, use a proportion. height of ∆XAB width of ∆XAB = height of ∆XYZ width of ∆XYZ 3 9 = x 6 9 x = 18, so x = 2 Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 4 Continued Step 3 To graph ∆XAB, first find the coordinate of A. The width is 2 units, and the height is 3 units, so the coordinates of A are (– 2, 3). Holt Algebra 2 Z Y A B X

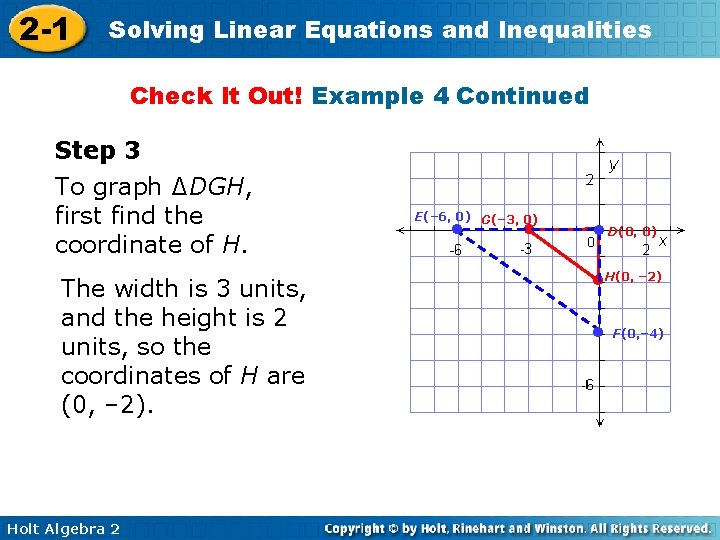
2 -1 Solving Linear Equations and Inequalities Check It Out! Example 4 ∆DEF has vertices D(0, 0), E(– 6, 0) and F(0, – 4). ∆DGH is similar to ∆DEF with a vertex at G(– 3, 0). Graph ∆DEF and ∆DGH on the same grid. Step 1 Graph ∆DEF. Then draw DG. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 4 Continued Step 2 To find the height of ∆DGH, use a proportion. width of ∆DGH = width of ∆DEF height of ∆DGH height of ∆DEF 3 x = 6 4 6 x = 12, so x = 2 Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 4 Continued Step 3 To graph ∆DGH, first find the coordinate of H. The width is 3 units, and the height is 2 units, so the coordinates of H are (0, – 2). Holt Algebra 2 E(– 6, 0) G(– 3, 0) ● ● ● D(0, 0) ●H(0, – 2) ● F(0, – 4)

2 -1 Solving Linear Equations and Inequalities Example 5: Nature Application The tree in front of Luka’s house casts a 6 -foot shadow at the same time as the house casts a 22 -fot shadow. If the tree is 9 feet tall, how tall is the house? Sketch the situation. The triangles formed by 9 ft using the shadows are similar, so Luka can use a proportion to find h the height of the house. 6 ft 6 22 = 9 h 6 h = 198 Shadow of tree Shadow of house = Height of tree Height of house h = 33 The house is 33 feet high. Holt Algebra 2 h ft 22 ft

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 5 A 6 -foot-tall climber casts a 20 -foot long shadow at the same time that a tree casts a 90 -foot long shadow. How tall is the tree? Sketch the situation. The triangles formed by using the shadows are similar, so the climber can use a proportion to find h the height of the tree. 20 90 = 6 h 6 ft 20 ft Shadow of climber Shadow of tree = Height of climber Height of tree 20 h = 540 h ft h = 27 The tree is 27 feet high. Holt Algebra 2 90 ft

2 -1 Solving Linear Equations and Inequalities Lesson Quiz: Part I Solve each proportion. 1. k=8 2. g = 42 3. The results of a recent survey showed that 61. 5% of those surveyed had a pet. If 738 people had pets, how many were surveyed? 1200 4. Gina earned $68. 75 for 5 hours of tutoring. Approximately how much did she earn per minute? $0. 23 Holt Algebra 2

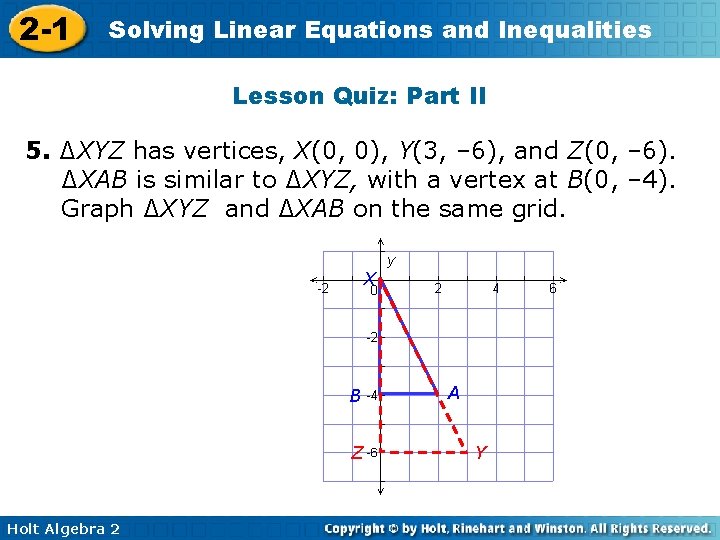
2 -1 Solving Linear Equations and Inequalities Lesson Quiz: Part II 5. ∆XYZ has vertices, X(0, 0), Y(3, – 6), and Z(0, – 6). ∆XAB is similar to ∆XYZ, with a vertex at B(0, – 4). Graph ∆XYZ and ∆XAB on the same grid. X B Z Holt Algebra 2 A Y

2 -1 Solving Linear Equations and Inequalities Lesson Quiz: Part III 6. A 12 -foot flagpole casts a 10 foot-shadow. At the same time, a nearby building casts a 48 -foot shadow. How tall is the building? 57. 6 ft Holt Algebra 2