Solving Function Optimization Problems with Genetic Algorithms September

Solving Function Optimization Problems with Genetic Algorithms September 26, 2001 Cho, Dong-Yeon dycho@bi. snu. ac. kr 301 -419, Tel: 880 -1847 © 2001 SNU CSE Biointelligence Lab
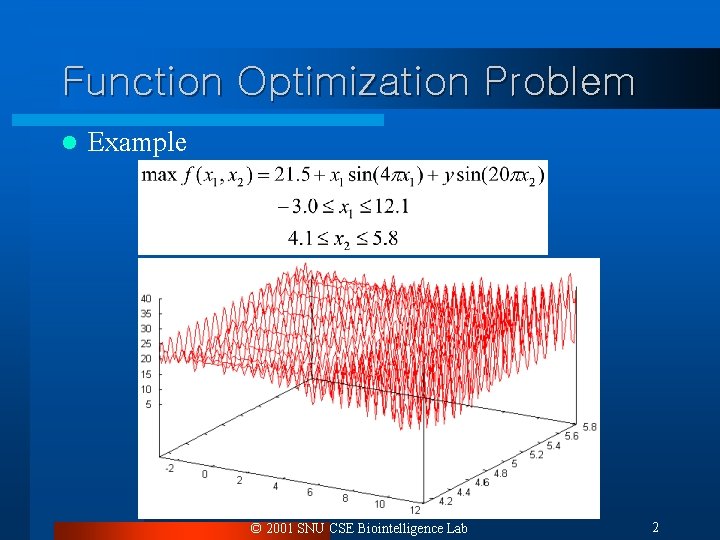
Function Optimization Problem l Example © 2001 SNU CSE Biointelligence Lab 2

Representation – Binary String l Code length © 2001 SNU CSE Biointelligence Lab 3

l Mapping from a binary string to real number x 1 x 2 Binary Number Decimal Number 0000010101001 5417 1011111110 © 2001 SNU CSE Biointelligence Lab 24318 4
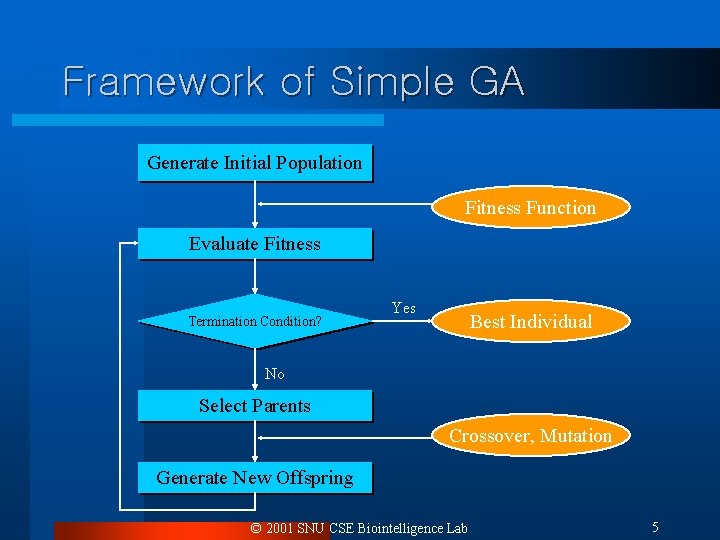
Framework of Simple GA Generate Initial Population Fitness Function Evaluate Fitness Termination Condition? Yes Best Individual No Select Parents Crossover, Mutation Generate New Offspring © 2001 SNU CSE Biointelligence Lab 5

Initial Population l Initial population is randomly generated. © 2001 SNU CSE Biointelligence Lab 6

Fitness Evaluation l Procedure: Evaluation ¨ Convert the chromosome’s genotype to its phenotype. < This means converting binary string into relative real values. ¨ Evaluate the objective function. ¨ Convert the value of objective function into fitness. < For the maximization problem, the fitness is simply equal to the value of objective function. < For the minimization problem, the fitness is the reciprocal of the value of objective function. © 2001 SNU CSE Biointelligence Lab 7

© 2001 SNU CSE Biointelligence Lab 8

Selection l Fitness proportional (roulette wheel) selection ¨ The roulette wheel can be constructed as follows. < Calculate the total fitness for the population. < Calculate selection probability pk for each chromosome vk. < Calculate cumulative probability qk for each chromosome vk. © 2001 SNU CSE Biointelligence Lab 9
![l Procedure: Proportional_Selection ¨ Generate a random number r from the range [0, 1]. l Procedure: Proportional_Selection ¨ Generate a random number r from the range [0, 1].](http://slidetodoc.com/presentation_image_h/ebb4ca45d71a9f064b1a8d18f20edc2f/image-10.jpg)
l Procedure: Proportional_Selection ¨ Generate a random number r from the range [0, 1]. ¨ If r q 1, then select the first chromosome v 1; else, select the kth chromosome vk (2 k pop_size) such that qk-1 < r qk. pk qk 1 0. 111180 2 0. 097515 0. 208695 3 0. 053839 0. 262534 4 0. 165077 0. 427611 5 0. 088057 0. 515668 6 0. 066806 0. 582475 7 0. 100815 0. 683290 8 0. 110945 0. 794234 9 0. 148211 0. 942446 10 0. 057554 1. 000000 © 2001 SNU CSE Biointelligence Lab 10

l Tournament Selection ¨ Repeat below procedure two times < Randomly < draw a tournament of size t from the population with replacement. Choose fittest program to be parent. © 2001 SNU CSE Biointelligence Lab 11

Genetic Operations l Crossover ¨ One point crossover ¨ Crossover rate pc l Procedure: Crossover ¨ Select two parents. ¨ Generate a random number rc from the range [0, 1]. ¨ If rc < pc then perform undergo crossover. l Mutation ¨ Mutation alters one or more genes with a probability equal to the mutation rate pm. © 2001 SNU CSE Biointelligence Lab 12

© 2001 SNU CSE Biointelligence Lab 13

Test Functions l Maximization (d=5) © 2001 SNU CSE Biointelligence Lab 14

l Minimization (d=5) ¨ Ackley’s function ¨ Rastrigin’s function ¨ Schwefel’s (sine root) function © 2001 SNU CSE Biointelligence Lab 15

Experiments (Minimum Requirements) l At least two test functions ¨ Maximization Problem ¨ One of the Minimization Problems l Various experimental setup ¨ Termination condition: maximum_generation ¨ 2 Selection Method 3 settings 10 runs < Proportional: Crossover and Mutation rate (pc, pm) < Tournament: Tournament size (t) ¨ Elitism < The best chromosome of the previous population is just copied. © 2001 SNU CSE Biointelligence Lab 16
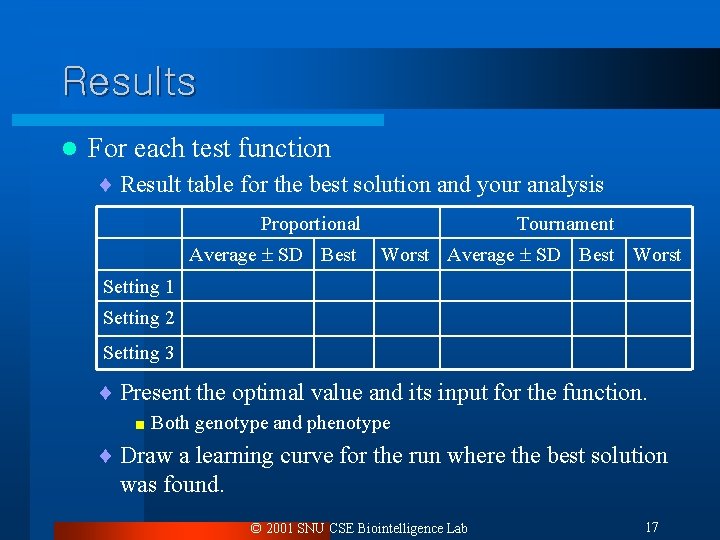
Results l For each test function ¨ Result table for the best solution and your analysis Proportional Average SD Best Tournament Worst Average SD Best Worst Setting 1 Setting 2 Setting 3 ¨ Present the optimal value and its input for the function. < Both genotype and phenotype ¨ Draw a learning curve for the run where the best solution was found. © 2001 SNU CSE Biointelligence Lab 17
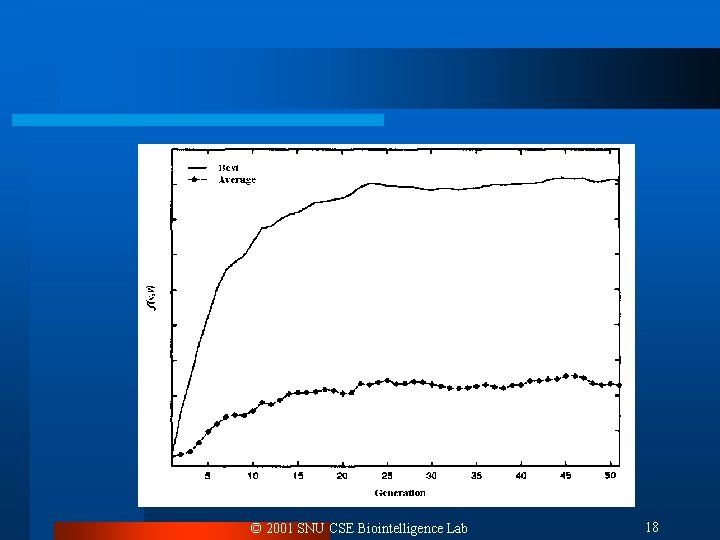
© 2001 SNU CSE Biointelligence Lab 18

References l Source Codes ¨ Simple GA coding ¨ GA libraries (C, C++, JAVA, …) ¨ MATLAB Tool box Web sites l Books l ¨ Genetic Algorithms and Engineering Design, Mitsuo Gen and Runwei Cheng, pp. 1 -15, John Wiley & Sons, 1997. ¨ Genetic algorithms in search, optimization, and machine learning, David E. Goldberg, Addison. Wesley, 1989. © 2001 SNU CSE Biointelligence Lab 19

Pay Attention! Due (October 17, 2001): By the end of class l Submission l ¨ Source code and executable file(s) < Proper comments in the source code < Via e-mail ¨ Report: Hardcopy!! < Running environments < Results for many experiments with various parameter settings < Analysis and explanation about the results in your own way © 2001 SNU CSE Biointelligence Lab 20

Bonus Problems l Maximization (d=30) ¨ 3 -deceptive function l Minimization (d=5) ¨ Rosenbrock’s function © 2001 SNU CSE Biointelligence Lab 21
- Slides: 21