Solving for Unknown Angles The Auxiliary Line Eureka



- Slides: 19

Solving for Unknown Angles: The Auxiliary Line Eureka Math: Geometry Modules 1 & 2 Lesson 7

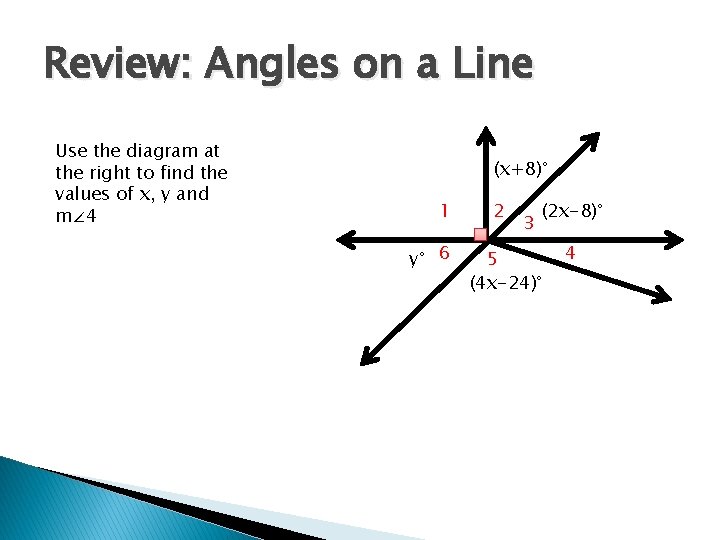
Review: Angles on a Line Use the diagram at the right to find the values of x, y and m∠ 4 (x+8)° 1 y° 6 2 3 (2 x-8)° 5 (4 x-24)° 4

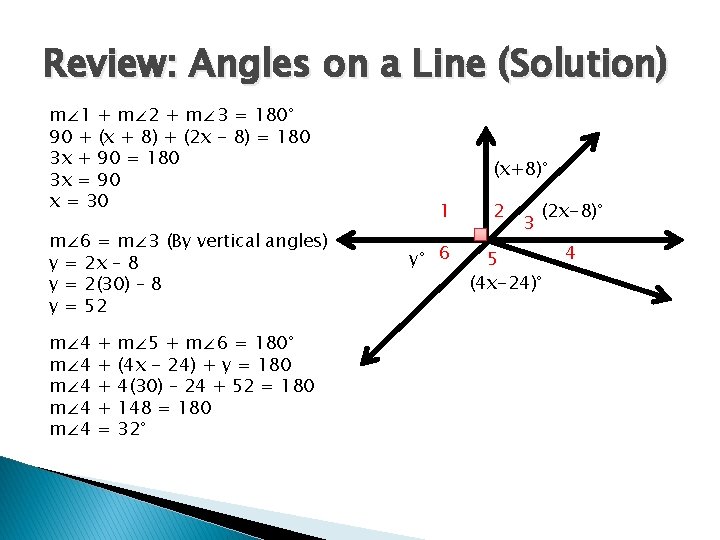
Review: Angles on a Line (Solution) m∠ 1 + m∠ 2 + m∠ 3 = 180° 90 + (x + 8) + (2 x - 8) = 180 3 x + 90 = 180 3 x = 90 x = 30 m∠ 6 = m∠ 3 (By vertical angles) y = 2 x – 8 y = 2(30) – 8 y = 52 m∠ 4 m∠ 4 + + = m∠ 5 + m∠ 6 = 180° (4 x - 24) + y = 180 4(30) – 24 + 52 = 180 148 = 180 32° (x+8)° 1 y° 6 2 3 (2 x-8)° 5 (4 x-24)° 4

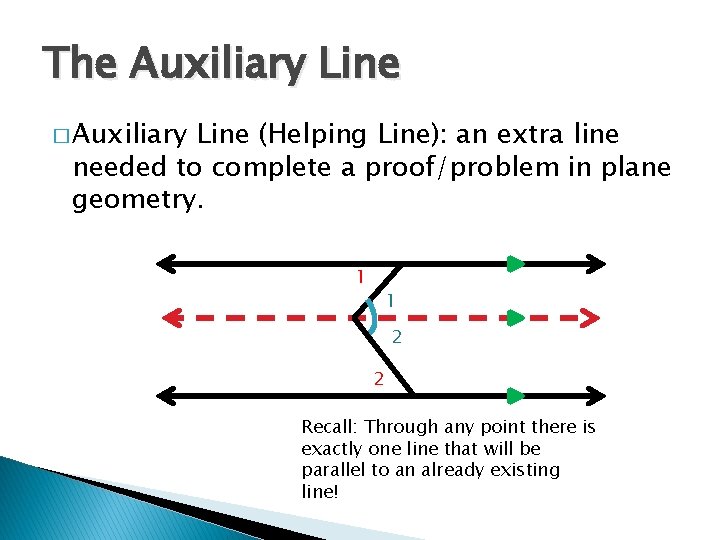
The Auxiliary Line � Auxiliary Line (Helping Line): an extra line needed to complete a proof/problem in plane geometry. 1 1 2 2 Recall: Through any point there is exactly one line that will be parallel to an already existing line!

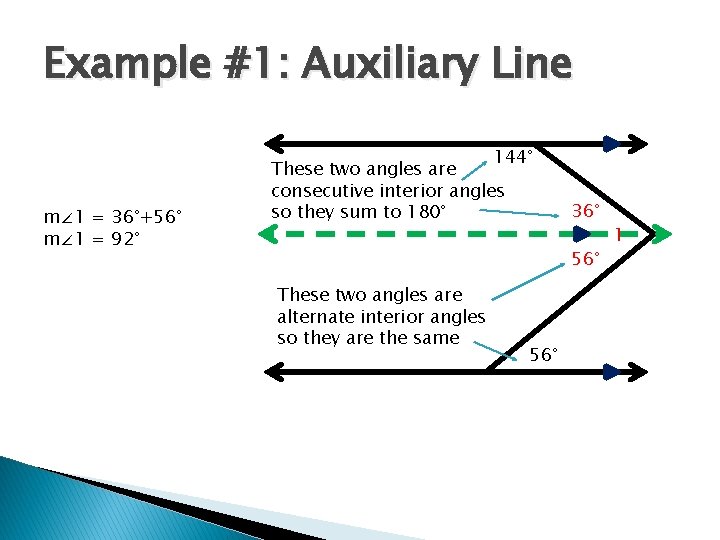
Example #1: Auxiliary Line m∠ 1 = 36°+56° m∠ 1 = 92° 144° These two angles are consecutive interior angles so they sum to 180° 36° 56° These two angles are alternate interior angles so they are the same 56° 1

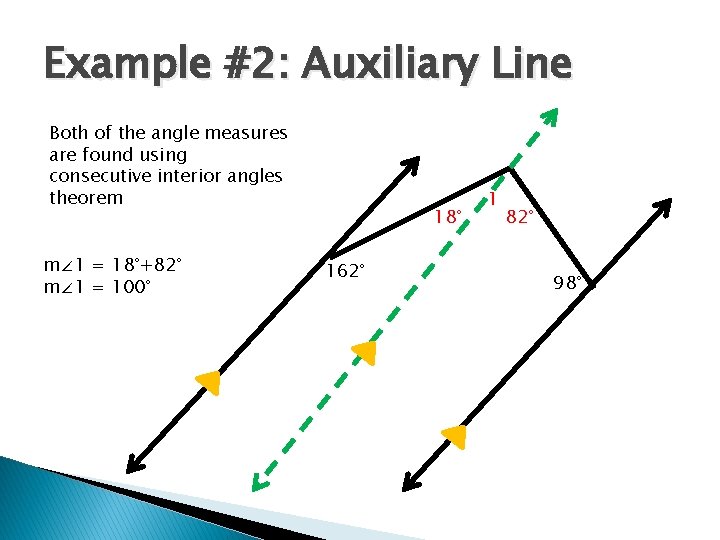
Example #2: Auxiliary Line Both of the angle measures are found using consecutive interior angles theorem m∠ 1 = 18°+82° m∠ 1 = 100° 18° 162° 1 82° 98°

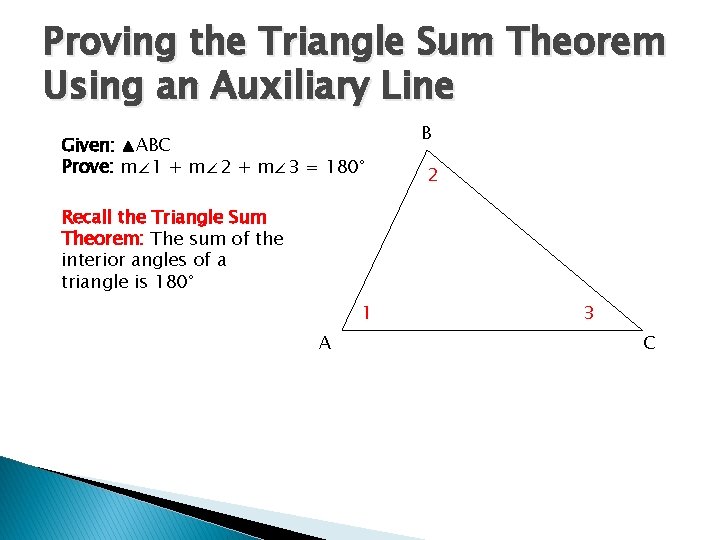
Proving the Triangle Sum Theorem Using an Auxiliary Line Given: ▲ABC Prove: m∠ 1 + m∠ 2 + m∠ 3 = 180° B 2 Recall the Triangle Sum Theorem: The sum of the interior angles of a triangle is 180° 1 A 3 C

Plan for the proof � Draw an auxiliary line through B that is parallel to AC. Name the new angles on this line ∠ 4 and ∠ 5 � Demonstrate that m∠ 4 + m∠ 2 + m∠ 5 = 180°, ∠ 1 ≅ ∠ 4 and ∠ 3 ≅ ∠ 5 � Use substitution to get m∠ 1 + m∠ 2 + m∠ 3 = 180°

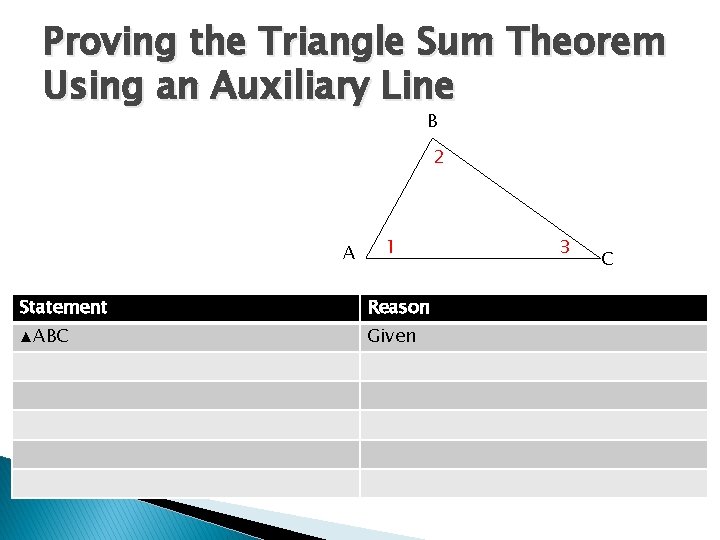
Proving the Triangle Sum Theorem Using an Auxiliary Line B 2 A 1 Statement Reason ▲ABC Given 3 C

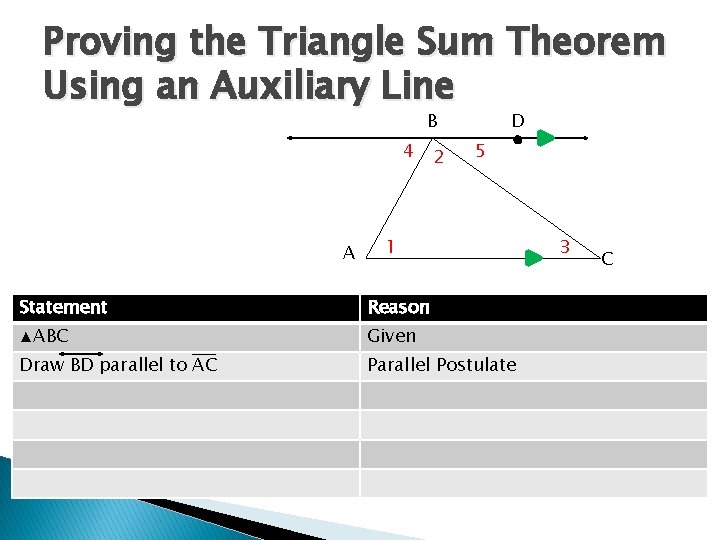
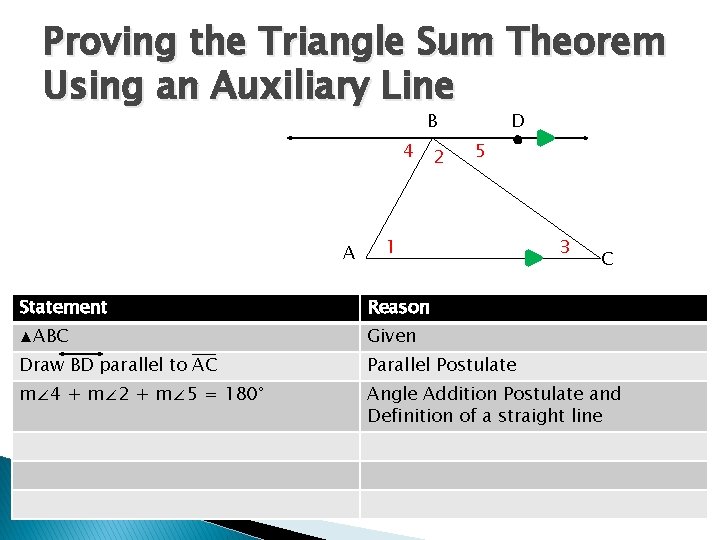
Proving the Triangle Sum Theorem Using an Auxiliary Line B 4 A 2 D 5 1 Statement Reason ▲ABC Given Draw BD parallel to AC Parallel Postulate 3 C

Proving the Triangle Sum Theorem Using an Auxiliary Line B 4 A 2 D 5 1 3 C Statement Reason ▲ABC Given Draw BD parallel to AC Parallel Postulate m∠ 4 + m∠ 2 + m∠ 5 = 180° Angle Addition Postulate and Definition of a straight line

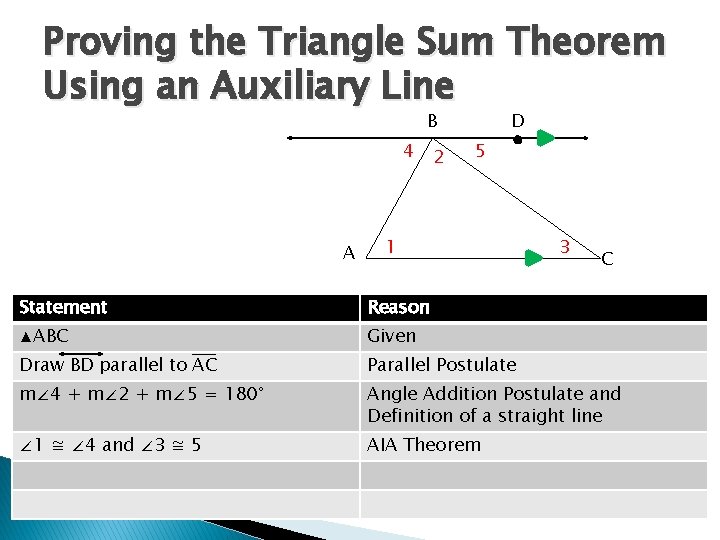
Proving the Triangle Sum Theorem Using an Auxiliary Line B 4 A 2 D 5 1 3 C Statement Reason ▲ABC Given Draw BD parallel to AC Parallel Postulate m∠ 4 + m∠ 2 + m∠ 5 = 180° Angle Addition Postulate and Definition of a straight line ∠ 1 ≅ ∠ 4 and ∠ 3 ≅ 5 AIA Theorem

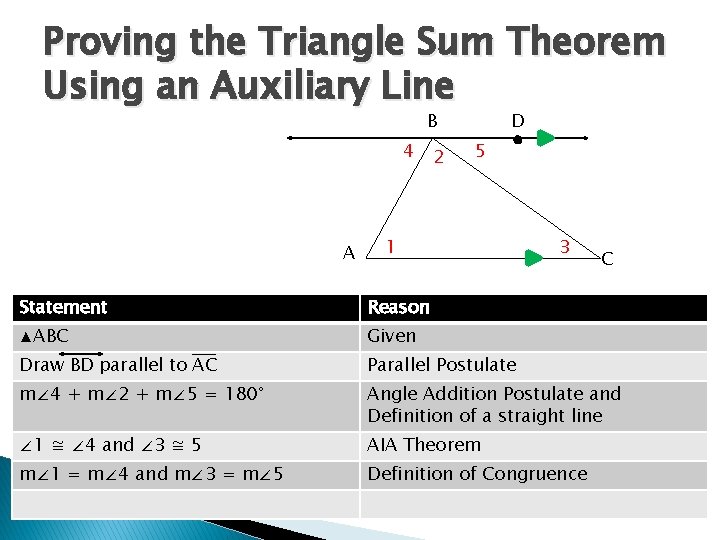
Proving the Triangle Sum Theorem Using an Auxiliary Line B 4 A 2 D 5 1 3 C Statement Reason ▲ABC Given Draw BD parallel to AC Parallel Postulate m∠ 4 + m∠ 2 + m∠ 5 = 180° Angle Addition Postulate and Definition of a straight line ∠ 1 ≅ ∠ 4 and ∠ 3 ≅ 5 AIA Theorem m∠ 1 = m∠ 4 and m∠ 3 = m∠ 5 Definition of Congruence

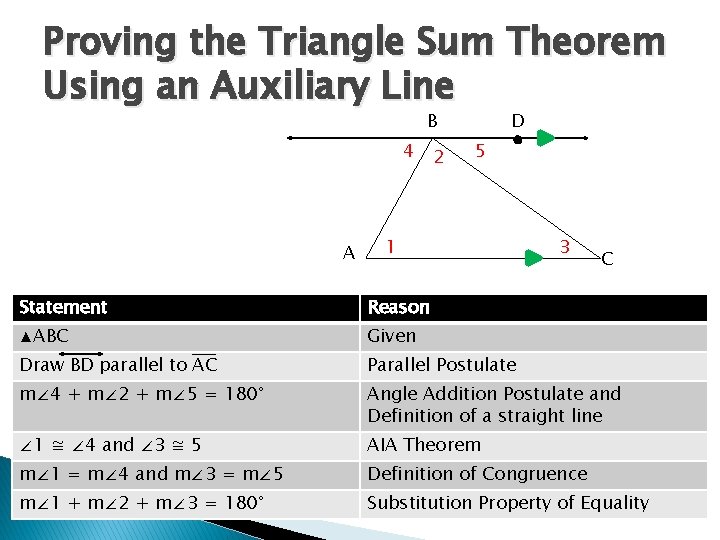
Proving the Triangle Sum Theorem Using an Auxiliary Line B 4 A 2 D 5 1 3 C Statement Reason ▲ABC Given Draw BD parallel to AC Parallel Postulate m∠ 4 + m∠ 2 + m∠ 5 = 180° Angle Addition Postulate and Definition of a straight line ∠ 1 ≅ ∠ 4 and ∠ 3 ≅ 5 AIA Theorem m∠ 1 = m∠ 4 and m∠ 3 = m∠ 5 Definition of Congruence m∠ 1 + m∠ 2 + m∠ 3 = 180° Substitution Property of Equality

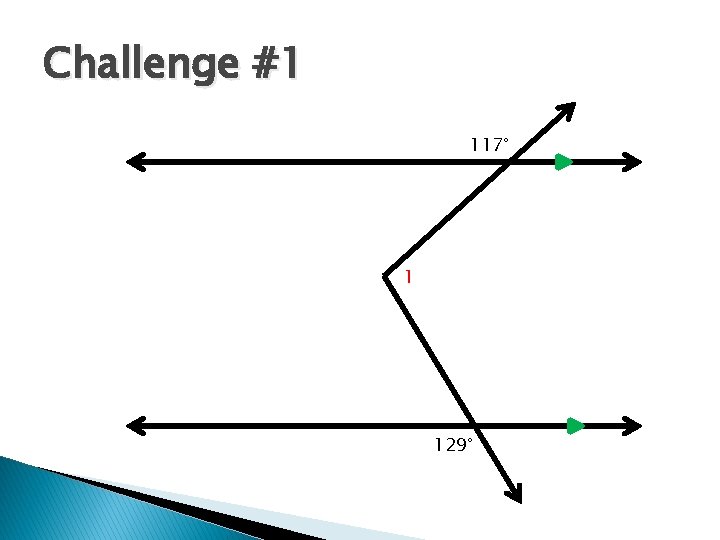
Challenge #1 117° 1 129°

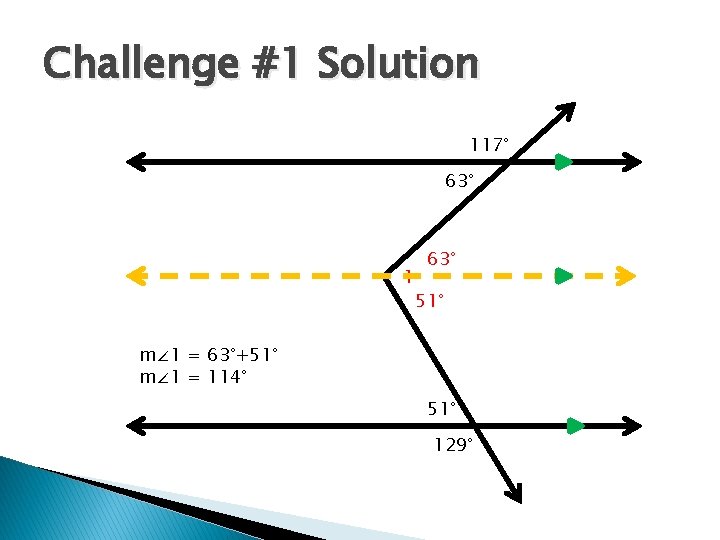
Challenge #1 Solution 117° 63° 1 63° 51° m∠ 1 = 63°+51° m∠ 1 = 114° 51° 129°

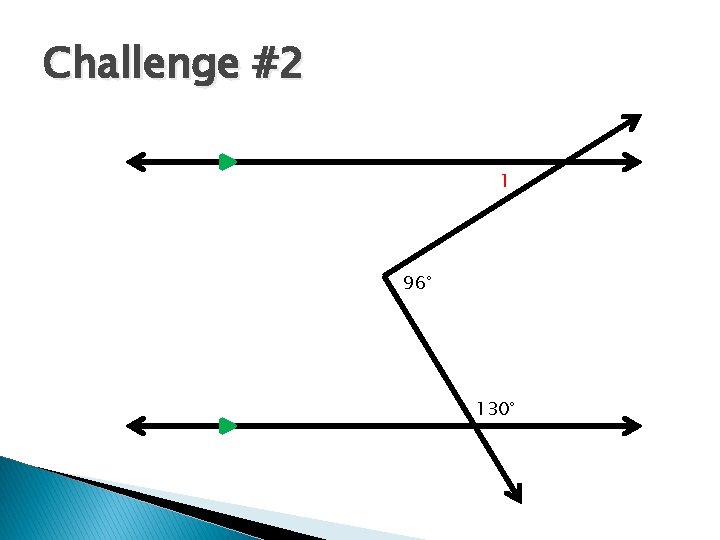
Challenge #2 1 96° 130°

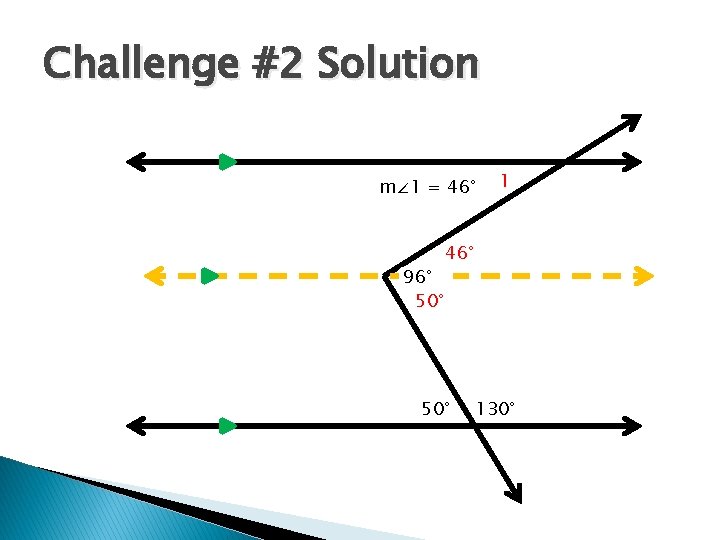
Challenge #2 Solution m∠ 1 = 46° 96° 50° 1 46° 50° 130°

Bibliography � Eureka Math: Geometry Module 1&2 � Big Ideas Geometry