SOLVING EQUATIONS USING ITERATIVE METHODS Learning Outcomes Know

SOLVING EQUATIONS USING ITERATIVE METHODS Learning Outcomes: • Know how to solve equations using Iterative Methods Step 1: Rewrite the equation in a more suitable form Step 2: Rewrite as an iterative sequence Step 3: Choose a starting value and iterate to see if our sequence converges to a solution

Example: Solve the equation using iterative methods Step 1: Rewrite the equation in a more suitable form See last lesson Step 2: Rewrite as an iterative sequence Step 3: Choose a starting value and iterate to see if our sequence converges to a solution x 0 0. 5 x 1 -3. 25 x 1 -1. 375 x 1 2 x 1 8 x 2 10. 8125 x 2 -0. 55469 x 2 2. 645751 x 2 2. 375 x 3 103. 0976563 x 3 -1. 34616 x 3 2. 879497 x 3 3. 263158 x 4 10523. 02907 x 4 -0. 59393 x 4 2. 95956 x 4 2. 919355 x 5 110723614. 7 x 5 -1. 32363 x 5 2. 986489 x 5 3. 027624 Diverges Converges to -1 Converges to 3

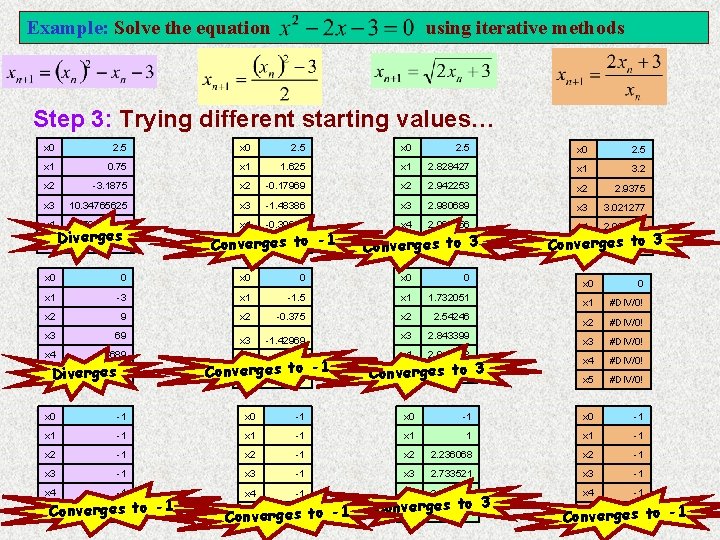
Example: Solve the equation using iterative methods Step 3: Trying different starting values… x 0 2. 5 x 1 0. 75 x 1 1. 625 x 1 2. 828427 x 1 3. 2 x 2 -3. 1875 x 2 -0. 17969 x 2 2. 942253 x 2 2. 9375 x 3 10. 34765625 x 3 -1. 48386 x 3 2. 980689 x 3 3. 021277 x 4 93. 72633362 x 4 -0. 39909 x 4 2. 993556 x 4 2. 992958 x 0 0 x 1 -3 x 1 -1. 5 x 1 1. 732051 x 2 9 x 2 -0. 375 x 2 2. 54246 x 3 69 -1. 42969 x 3 2. 843399 x 4 4689 -0. 478 x 4 2. 947338 erges x 5 Div 8687. 89928 ges x 5 Diver 21982029 x 5 rg-1. 42037 es to -1 Conve x 3 x 4 to -1 rges Conve x 5 -1. 38576 2. 997851 to 3 Convex 5 rges es to 3 x 5 rg 2. 982394 Conve es to 3 x 5 rg 3. 002353 Conve x 0 0 x 1 #DIV/0! x 2 #DIV/0! x 3 #DIV/0! x 4 #DIV/0! x 5 #DIV/0! x 0 -1 x 1 -1 x 1 -1 x 2 2. 236068 x 2 -1 x 3 2. 733521 x 3 -1 x 4 2. 909818 x 4 -1 x 5 -1 to -1 Converges Conx 5 verges-1 to -1 es to 3 Conve x 5 rg 2. 969787 Conx 5 verges-1 to -1

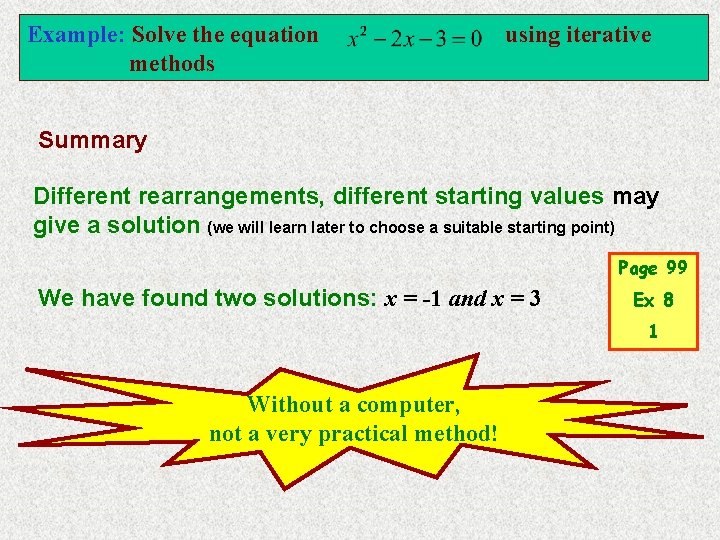
Example: Solve the equation methods using iterative Summary Different rearrangements, different starting values may give a solution (we will learn later to choose a suitable starting point) Page 99 We have found two solutions: x = -1 and x = 3 Ex 8 1 Without a computer, not a very practical method!

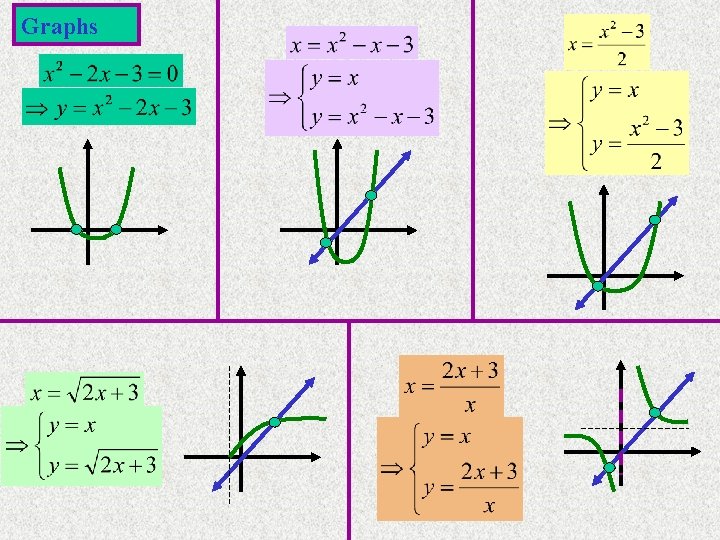
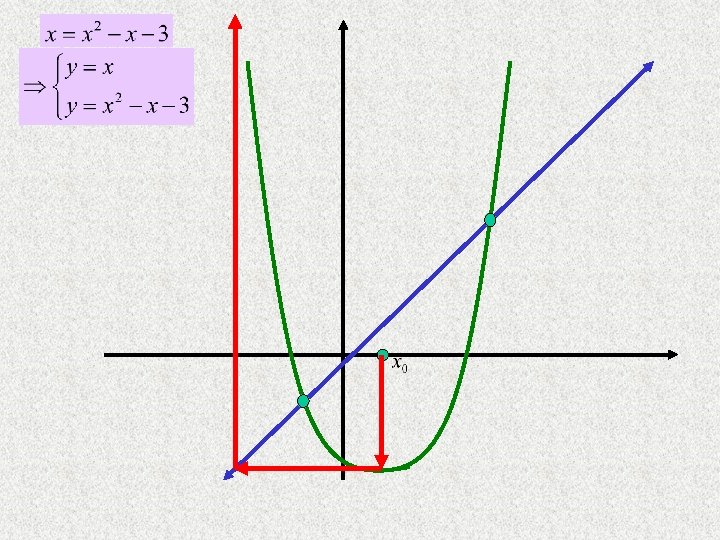
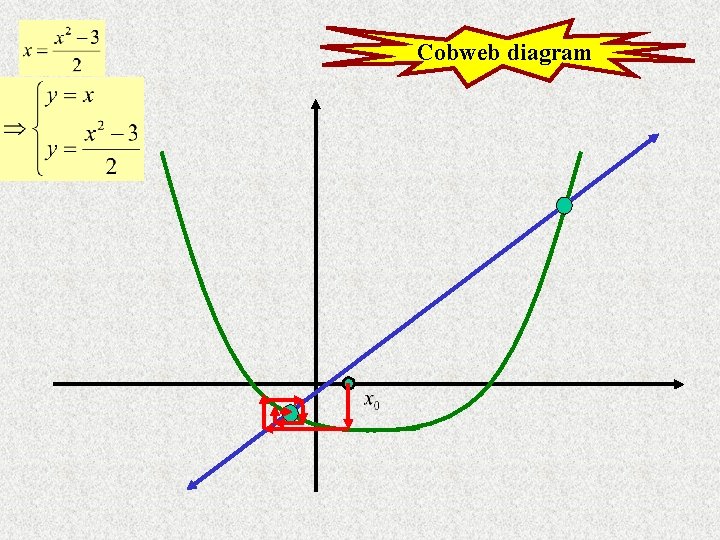
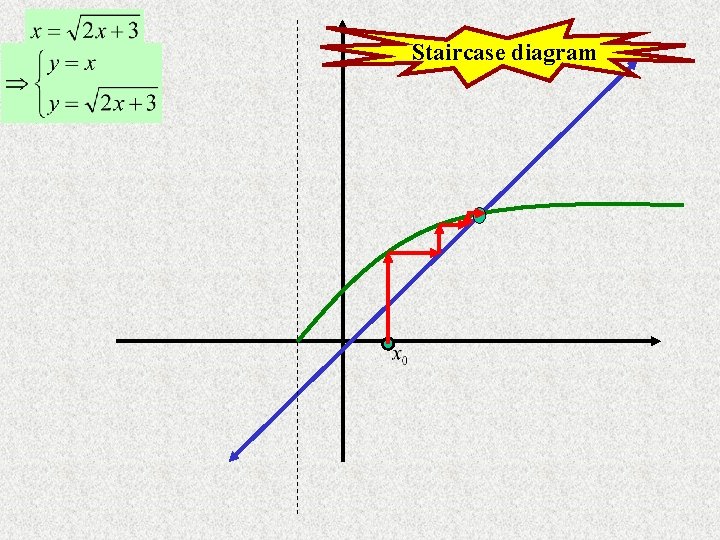
Graphs

Cobweb diagram

Staircase diagram