Solving Equations Translate verbal expressions into algebraic expression

Solving Equations Ø Translate verbal expressions into algebraic expression and equations and vice versa. Ø Solve equations using the properties of equality. 1) open sentence 2) equation 3) solution

Solving Equations A mathematical sentence (expression) containing one or more variables is called an open sentence. A mathematical sentence stating that two mathematical expressions are equal equation is called an _____. Open sentences are neither true nor false until the variables have been replaced by numbers. Each replacement that results in a true statement is called a ____ solution of the open sentence.

Solving Equations To solve equations, we can use properties of equality. Some of these equivalence relations are listed in the following table. Properties of Equality Property Reflexive Symmetric Transitive Substitution Symbol For any real number a, a = a, For all real numbers a and b, If a = b, then b = a Example – 5+y=– 5+y If 3 = 5 x – 6, then 5 x – 6 = 3 For all real numbers a, b, and c. If 2 x + 1 = 7 and 7 = 5 x – 8 If a = b, and b = c, then a = c then, 2 x + 1 = 5 x – 8 If a = b, then a may be replaced by b and b may be replaced by a. If (4 + 5)m = 18 then 9 m = 18

Solving Equations Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Addition and Subtraction Properties of Equality For any real numbers a, b, and c, if a = b, then a -c = b -c a +c = b +c Example: If x – 4 = 5, then x– 4 +4 =5 +4 If n + 3 = – 11, then n + 3 – 3 = – 11 – 3

Solving Equations Sometimes an equation can be solved by adding the same number to each side or by subtracting the same number from each side or by multiplying or dividing each side by the same number. Multiplication and Division Properties of Equality For any real numbers a, b, and c, if a = b, then a = b c c a·c = b ·c Example: 4 4 -3 -3

Chapter 5: Solving Equations • What will we discuss? ü What are the parts of an equation ü What does it mean to solve an equation ü How do we use inverse operations to solve equations ü How to solve simple and complex equations

What Does it Mean to Solve an Equation? n n To solve an equation means to find every number that makes the equation true. We do this by adding or subtracting to each side of the equation … but always keep it balanced!

What are the parts of an equation? n Let’s first take a look at an equation and identify its parts Coefficient Constant Variable

So do we just use trial and error to find the right value? No. n We can use inverse operations to isolate, or solve for, the variable’s value. n Inverse operations? Think about it … The inverse operation of addition is subtraction. And the inverse operation of multiplication is division. n

Solving 1 Step Equations How much does the suitcase weigh in terms of blocks? B=Blocks S=Suitcase Equation: 6 B + S = 9 B -6 B S = 3 B What is the weight of the suitcase if each block has a weight of 2 lbs. ? S = 3 (2) = 6 lbs.

So how do we solve equations with inverse operations? n Let’s take a look at a simple equation Step 1: Answer: - 13 Now that we have solved the equation, let’s check the solution:

So how do we solve equations with inverse operations? n Let’s take a look at a simple equation Step 1: Answer: +5 +5 Now that we have solved the equation, let’s check the solution:

So how do we solve equations with inverse operations? n Let’s take a look at a simple equation Step 1: 25 Step 2: Answer: 25 Now that we have solved the equation, let’s check the solution:

So how do we solve equations with inverse operations? n Let’s take a look at a simple equation Step 1: (16) Step 2: Answer: (16) Now that we have solved the equation, let’s check the solution:

1 Step Equation X + 11 = 9 -11 = -2 X X - 37 = 52 20 + h = 41 17 - s = 27 This is the same as -1 S=10 1 3 X = 72 13 3 X = 24

1 Step Equations Continued… 1 6 X = 42 6 16 1 X=7 or x = 7 Cross Multiply 2 P= 3 5 4 Multiply by the reciprocal of 2/5

Multi Step Equations Solve: 8 m – 10 = 36 + 10 8 m = 46 8 8 m=

Multi Step Equations Solve: 5 x 2 = x + 4 +2 +2 5 x = x + 6 –x –x 4 x = 6 4 4 x= Notice that there are variables on both sides Get rid of the -2 on the left side Simplify Get rid of the x on the right side Simplify Get rid of the coefficient of x Simplify

Solving a Proportion n Solve the proportion below 12 12

Solving a Proportion n Solve the proportion below 52 52

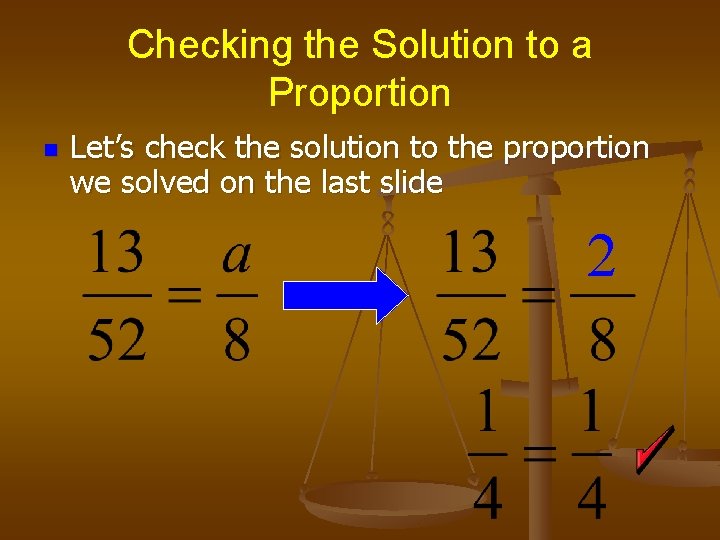
Checking the Solution to a Proportion n Let’s check the solution to the proportion we solved on the last slide 2

Using Proportions to Solve Problems n You get 46 miles to a gallon of gas. How far can you go on 16 gallons of gas?

Multi-step Solutions n Let’s take a look at our original equation Step 1: Step 2: -12 +x +x Step 3: 4 Answer: 4

Multi-step Solutions (involving distribution) n Consider the following equation Step 1: Step 2: +30 Step 3: 6 Answer: 6

Finding Variations of Formulas Solve the formula for r.