Solving Equations involving Brackets Lesson Objective To explain

Solving Equations involving Brackets

Lesson Objective To explain how to solve an equation that has brackets Lesson Success Criteria Knows how to expand the brackets, collect like terms, isolate and solve for the variable of interest

Example Solve 3(x – 2) = 6 x + 3 3 x - 6 = 6 x + 3 3 x + 3 = -6 3 x = -9 x = -3 This requires the brackets to be expanded Expanded out Subtracted 3 x from both sides, and swapped so the x term is on the LHS Subtract 3 from both sides Divide both sides by 3 ANSWER

Example Solve 5(x – 3) + 3 x = -7 5 x – 15 + 3 x = -7 8 x -15 = -7 8 x = 8 x=1 This requires the brackets to be expanded Expanded out Group like terms (for x) together Add 15 to both sides Divide both sides by 8 ANSWER

Example Solve 4(2 x – 1) + 5 = 2(3 x – 1) 8 x – 4 + 5 = 6 x - 2 2 x + 1 = -2 2 x = -3/2 This requires the brackets to be expanded Expanded out both sides Group like terms (for x) together on LHS Subtract 1 from both sides Divide both sides by 2 ANSWER

Example Sometimes you can choose whether or not to expand the brackets Solve 6(2 x + 1) = 12 ÷ 6 or Solve 6(2 x + 1) = 12 Expand out 2 x + 1 = 2 12 x + 6 = 12 -1 -6 2 x = 1 12 x = 6 ÷ 2 ÷ 12 ÷ 2 x = 1/2 ÷ 12 x = 1/2 Same answer, but two different ways of getting there
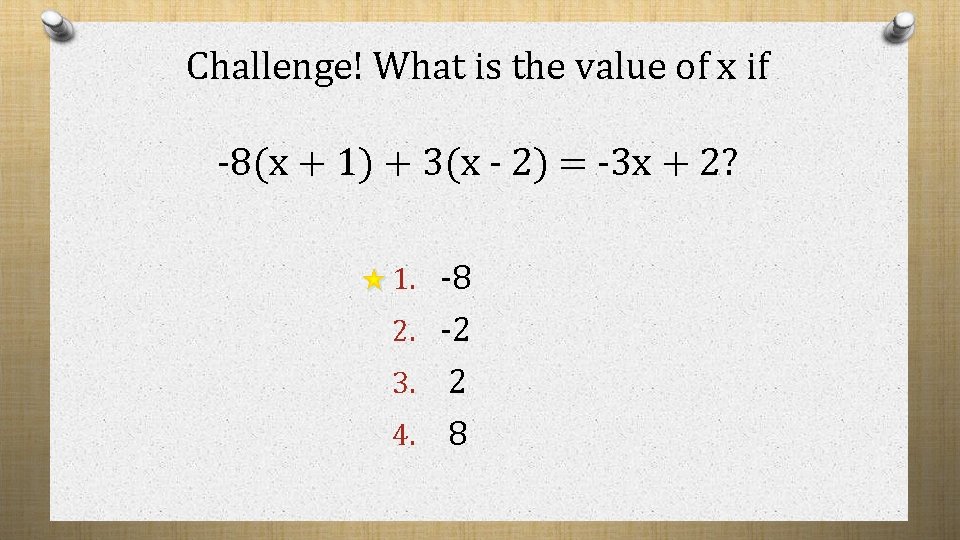
Challenge! What is the value of x if -8(x + 1) + 3(x - 2) = -3 x + 2? 1. -8 2. -2 2 4. 8 3.

Special Case #1 Solve 2 x + 5 = 2 x – 3 5 = -3 This is never true NO SOLUTION Special Case #2 Solve 3(x + 1) - 5 = 3 x – 2 3 x + 3 – 5 = 3 x – 2 -2 = -2 This is always true INFINITE SOLUTIONS

Homework Solving Linear Equations Exercise L: Page 51
- Slides: 9