Solving Equations by Graphing xintercept Method Move all

Solving Equations by Graphing - x-intercept Method • Move all terms to the left hand side of the equation, so that zero is on the right hand side. • Let Y 1 = left hand side of the equation. Example Solve the equation:

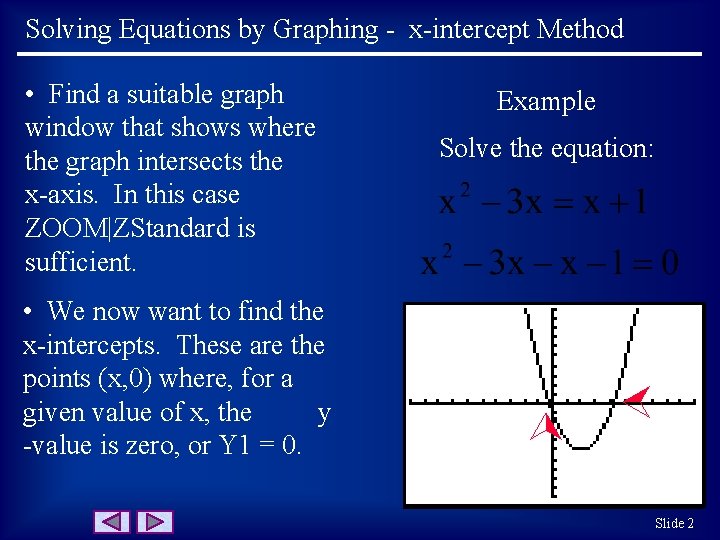
Solving Equations by Graphing - x-intercept Method Solve the equation: • We now want to find the x-intercepts. These are the points (x, 0) where, for a given value of x, the y -value is zero, or Y 1 = 0. Example • Find a suitable graph window that shows where the graph intersects the x-axis. In this case ZOOM|ZStandard is sufficient. Slide 2

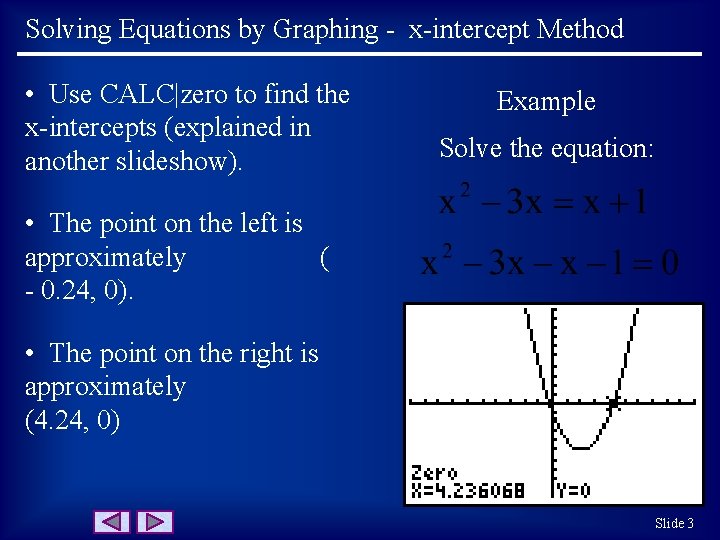
Solving Equations by Graphing - x-intercept Method • Use CALC|zero to find the x-intercepts (explained in another slideshow). Example Solve the equation: • The point on the left is approximately ( - 0. 24, 0). • The point on the right is approximately (4. 24, 0) Slide 3

Solving Equations by Graphing - x-intercept Method • Approximate solutions to the equation are x = - 0. 24, 4. 24. • To confirm that these are correct solutions, use TABLE. • TBLSET, Ask • TABLE • Enter the two x-values in the x-column and notice that the values in the Y 1 column are approximately zero, as they should be. Slide 4

Solving Equations by Graphing - x-intercept Method • The solutions just found were to the equation Example Solve the equation: • Note that these are the same x-values that satisfy the original equation Slide 5

Return to Table of Contents