Solving Compound Inequalities The inequalities you have seen

Solving Compound Inequalities The inequalities you have seen so far are simple inequalities. When two simple inequalities are combined into one statement by the words AND or OR, the result is called a compound inequality. Holt Mc. Dougal Algebra 1

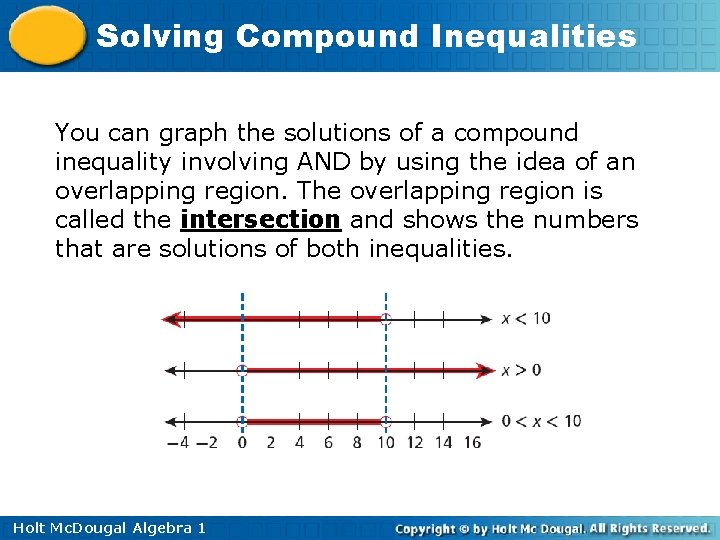
Solving Compound Inequalities You can graph the solutions of a compound inequality involving AND by using the idea of an overlapping region. The overlapping region is called the intersection and shows the numbers that are solutions of both inequalities. Holt Mc. Dougal Algebra 1

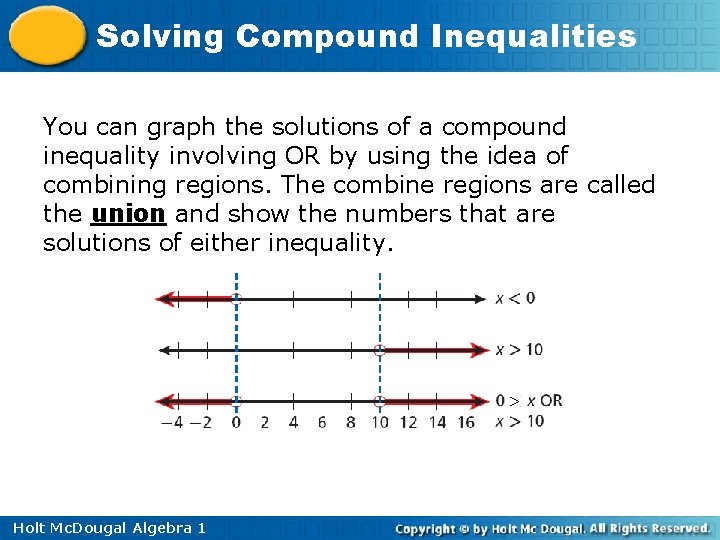
Solving Compound Inequalities You can graph the solutions of a compound inequality involving OR by using the idea of combining regions. The combine regions are called the union and show the numbers that are solutions of either inequality. > Holt Mc. Dougal Algebra 1

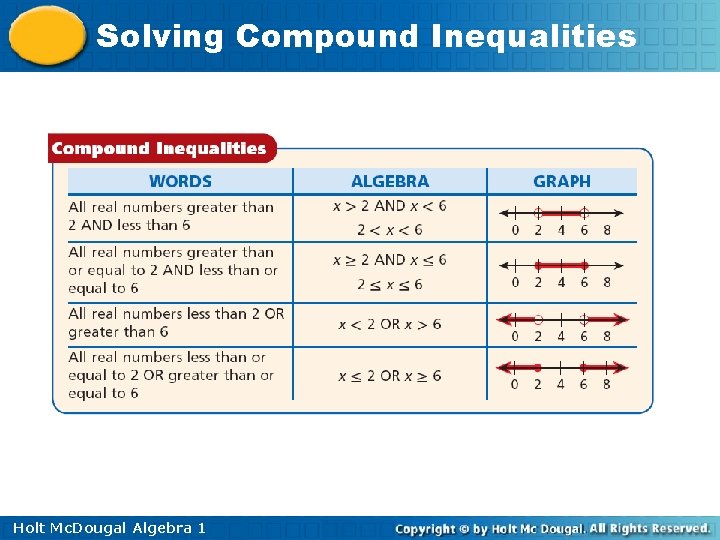
Solving Compound Inequalities Holt Mc. Dougal Algebra 1

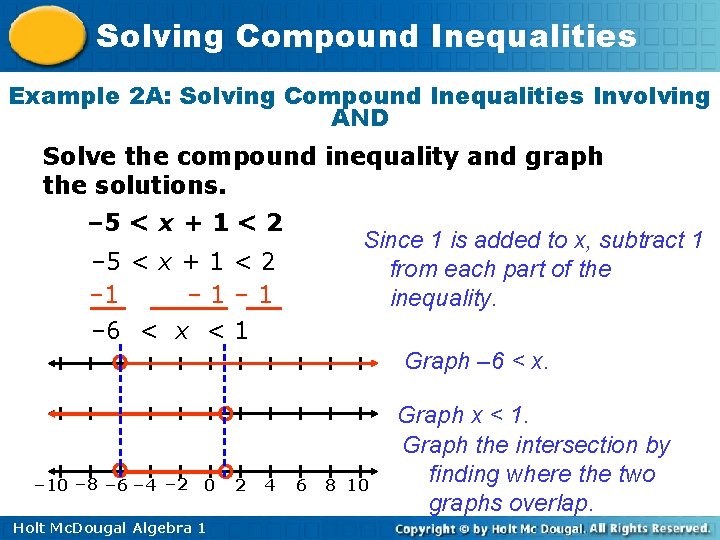
Solving Compound Inequalities Example 2 A: Solving Compound Inequalities Involving AND Solve the compound inequality and graph the solutions. – 5 < x + 1 < 2 Since 1 is added to x, subtract 1 from each part of the inequality. – 5 < x + 1 < 2 – 1– 1 – 6 < x < 1 Graph – 6 < x. – 10 – 8 – 6 – 4 – 2 0 Holt Mc. Dougal Algebra 1 2 4 6 8 10 Graph x < 1. Graph the intersection by finding where the two graphs overlap.

Solving Compound Inequalities Example 2 B: Solving Compound Inequalities Involving AND Solve the compound inequality and graph the solutions. 8 < 3 x – 1 ≤ 11 +1 +1 +1 9 < 3 x ≤ 12 3<x≤ 4 Holt Mc. Dougal Algebra 1 Since 1 is subtracted from 3 x, add 1 to each part of the inequality. Since x is multiplied by 3, divide each part of the inequality by 3 to undo the multiplication.

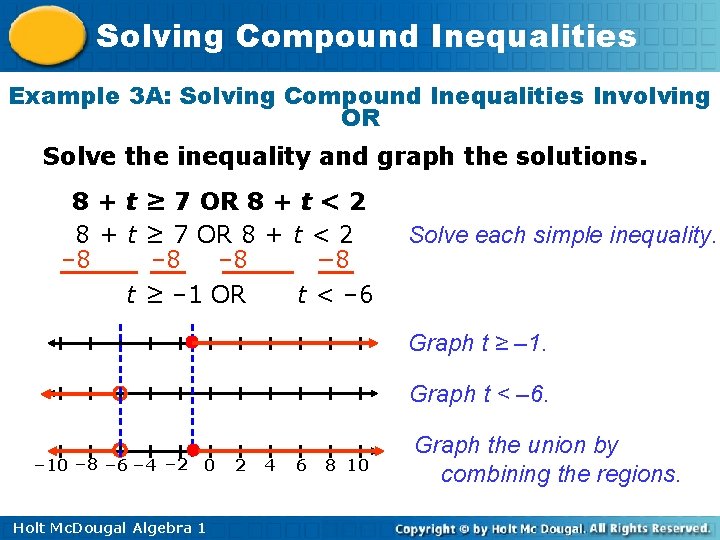
Solving Compound Inequalities Example 3 A: Solving Compound Inequalities Involving OR Solve the inequality and graph the solutions. 8 + t ≥ 7 OR 8 + t < 2 – 8 – 8 − 8 t ≥ – 1 OR t < – 6 Solve each simple inequality. Graph t ≥ – 1. Graph t < – 6. – 10 – 8 – 6 – 4 – 2 0 Holt Mc. Dougal Algebra 1 2 4 6 8 10 Graph the union by combining the regions.

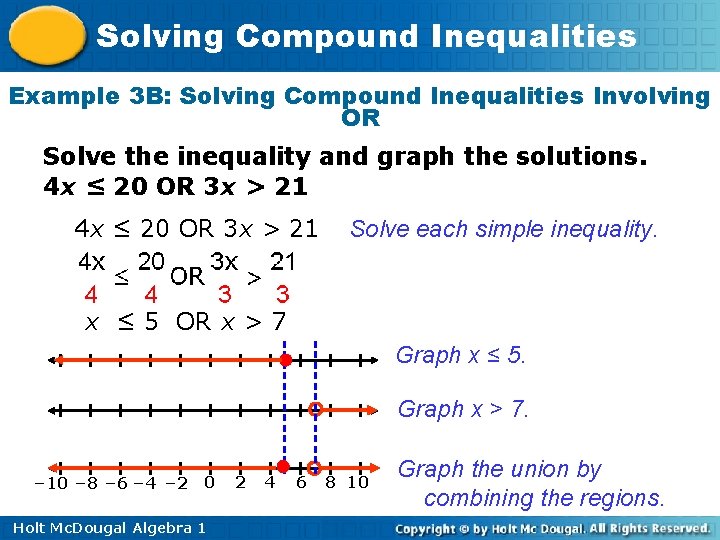
Solving Compound Inequalities Example 3 B: Solving Compound Inequalities Involving OR Solve the inequality and graph the solutions. 4 x ≤ 20 OR 3 x > 21 Solve each simple inequality. x ≤ 5 OR x > 7 Graph x ≤ 5. Graph x > 7. – 10 – 8 – 6 – 4 – 2 0 Holt Mc. Dougal Algebra 1 2 4 6 8 10 Graph the union by combining the regions.

Solving Compound Inequalities Example 4 A: Writing a Compound Inequality from a Graph Write the compound inequality shown by the graph. The shaded portion of the graph is not between two values, so the compound inequality involves OR. On the left, the graph shows an arrow pointing left, so use either < or ≤. The solid circle at – 8 means – 8 is a solution so use ≤. x ≤ – 8 On the right, the graph shows an arrow pointing right, so use either > or ≥. The empty circle at 0 means that 0 is not a solution, so use >. x > 0 The compound inequality is x ≤ – 8 OR x > 0. Holt Mc. Dougal Algebra 1

Solving Compound Inequalities Example 4 B: Writing a Compound Inequality from a Graph Write the compound inequality shown by the graph. The shaded portion of the graph is between the values – 2 and 5, so the compound inequality involves AND. The shaded values are on the right of – 2, so use > or ≥. The empty circle at – 2 means – 2 is not a solution, so use >. m > – 2 The shaded values are to the left of 5, so use < or ≤. The empty circle at 5 means that 5 is not a solution so use <. m<5 The compound inequality is m > – 2 AND m < 5 (or -2 < m < 5). Holt Mc. Dougal Algebra 1