SOLVING AND GRAPHING QUADRATIC INEQUALITIES Using the following

SOLVING AND GRAPHING QUADRATIC INEQUALITIES Using the following methods: • Case method • Test point method • Conjunction/Disjunction method

Graph the solution set of Case Method Factor first Now we should think in terms of multiplying. We are multiplying two numbers and we get a negative number. Case I : First factor is positive and second factor is negative

Case I : First factor is positive and second factor is negative AND This is impossible, as a number cannot be greater tha 1 and smaller than negative 1. So we reject this case. Case II : First factor is negative and second factor is positive AND

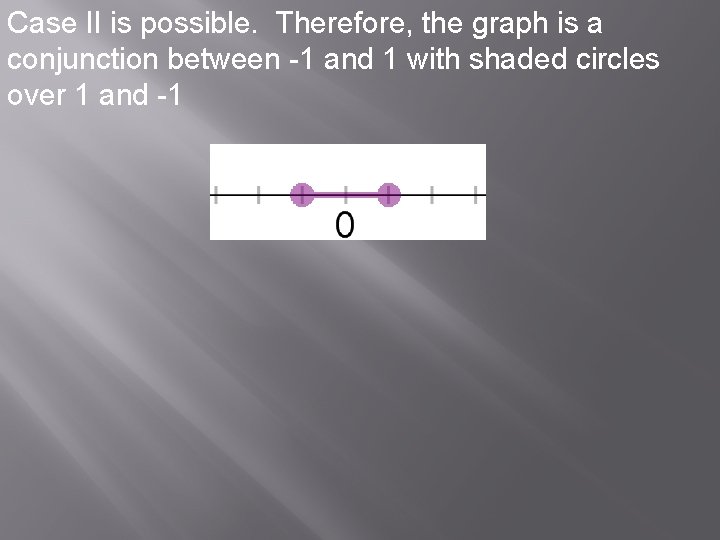
Case II is possible. Therefore, the graph is a conjunction between -1 and 1 with shaded circles over 1 and -1

Test point Method Start from the factored form. Treat it as an equation and solve for x Plot your zeros on a number line.

Place closed/shaded circles over our zeroes since the problem was less than or equal to. There are 3 regions we have to consider: The region before -1 The region after 1 The region between -1 and 1

For each region, choose a test point. For the region before -1, choose x = -2 (we could have chosen any number less than -1) Substitute your test point into the factored expression: The number we get is irrelevant, we only care about the sign. So any point chosen before -1 will give a positive number. We’ll mark this on our number line.

Choose a test point for the region between -1 and 1. 0 is a nice choice here. This tells us than any number chosen in this region will yield a negative number. Let’s mark that on our number line.

For the last region of greater than 1, choose x = 2. Again, any number greater than 1 would suffice. This tells us than any number in this region will yield a positive number. Like before, let’s mark this on our number line.

Now let’s go back to our factored form. The inequality sign tells us that our solution set is a number x that will make the expression negative (less than or equal to 0) If we look at our graph, the only region that happens is the region between -1 and 1 Therefore, we choose this region. Our final graph then is:

Conjunction/Disjunction Method (aka Quick Method) � This final method is the fastest, but use it very cautiously

Start with the factored form, just like all other methods Treat it like an equation, like the test point method, and plot your zeroes. Now look back at your inequality in factored form and recall absolute value inequalities. Greater than and greater than or equal to meant your graph will be a disjunction. Less than or less than or equal to implied a conjunction. We have a conjunction, therefore we shade the region between our “zeroes” (-1 and 1 here) as this would be a conjunction.

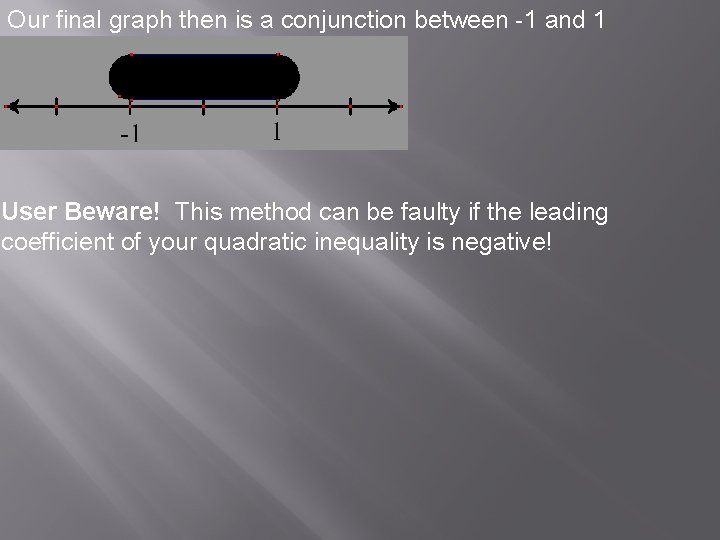
Our final graph then is a conjunction between -1 and 1 User Beware! This method can be faulty if the leading coefficient of your quadratic inequality is negative!

Risk of last method Example – Solve and graph the following: Treating like an equation and solving we get: Looking back at the original, this suggests that the graph is a disjunction (because it is greater than 0). But the actual graph is a conjunction between 2 and 3

To ensure that the last method will always work, we need to make sure that our coefficient of x^2 is positive. We can do this by multiplying by a negative one. Remember: when dividing or multiplying by a negative number, we flip the inequality sign Treating like an equation, we get that x = 2 or x = 3 But this time, we see that our graph is really a conjunction (since our expression is less than zero).